In August, 2010, [Alexander Yee] and [Shigeru Kondo] won a respectable amount of praise for calculating pi to more digits than anyone else. They’re back again, this time doubling the number of digits to 10 Trillion.
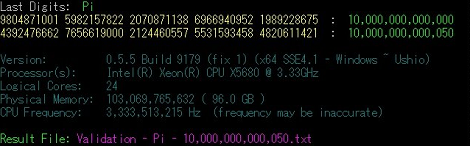
The previous calculation of 5 Trillion digits of Pi took 90 days to calculate on a beast of a workstation. The calculations were performed on 2x Xeon processors running at 3.33 GHz, 96 Gigabytes of RAM, and 32 Terabytes worth of hard drives. The 10 Trillion digit attempt used the same hardware, but needed 48 Terabytes of disk to store everything.
Unfortunately, the time needed to calculate 10 Trillion digits didn’t scale linearly. [Alex] and [Shigeru] waited three hundred and seventy-one days for the computer to finish the calculations. The guys used y-cruncher, a multithreaded pi benchmarking tool written by [Alex]. y-cruncher calculates hexadecimal digits of pi; conveniently, it’s fairly easy to find the nth hex digit of pi for verification.
If you’re wondering if it would be faster to calculate pi on a top 500 supercomputer, you’d be right. Those boxes are a little busy predicting climate change, nuclear weapons yields, and curing cancer, though. Doing something nobody else has ever done is still an admirable goal, especially if it means building an awesome computer.















What kind of calculations do you think they need that much precision for? :)
exactly why i came to post here! other than “because he can” explanation….why?!?!
Ever read Contact by Carl Sagan? It’s not in base 11, but it’s a start.
doesn’t matter, it’s pi and pi is awesome, rivaled only by tau
It’s the last digit, not number. The number is the whole thing. Sorry, am narrowminded today..
Well I want to know if the last digit is the number 5 (you know decimal) or 0x05 (hex)
0x05 == 5… Or did I miss a memo?
On their website I spotted this
Pi – Computation
371 days
Start : 10:34 AM (JST) October 10, 2010
Finish: 3:14 PM (JST) October 16, 2011
Kinda lucky end time coincidence… ;-)
MAN….you ruined the ending i was going to do that tomorrow… DANG IT
I wish I had 96 gigabytes of ram…. I could run my entire laptop off that much ram….
What about this: http://www.ebay.com/itm/IBM-X3755-4-X-OPTERON-8218-2-6GHZ-128GB-RAM-5-X-146GB-15K-SAS-/170730185328?pt=COMP_EN_Servers&hash=item27c04fe270#ht_775wt_1344
If you read the page it says they lost 180 days due to hardware failure. So it really only took 191 days of computation. That’s nearly linear time.
How can this number be so long? Is it infinite?
In a parallel universe, could Pi be a finite number?
Is God gonna be mad if we find all the decimal of Pi?
pi is infinite we cant find all of pi it is iiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiinnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnfffffffffffffffffffffffffffffffffffffffffffffffffffffffffiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiinnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnniiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiitttttttttttttttttttttttttttttttttttttttttttttttteeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeee
Now how long would it take on several GPUs?
I was wondering this too. String up a few GTX560’s and write a nice little CUDA PI program and let it fly.
You forgot to say what the value of pi is on this page.
So here are the first 32 digits.
3.1415926535897932384626433832795???
Can you please post the first 32 thousand digits.
Found a few more digits of pi:
3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679
25976919716538537682796308295009093877333987211875This comment has been modified because: Not accurate after 100 decimal places. Be more careful next time -BrianWhat is the point?
The point is the little dot between the 3 and the 1…
Three point one four one five nine two six…
My inductive and capacitive reactance calculations will henceforth be more accurate.
https://github.com/philipl/pifs
http://latkin.org/blog/2012/11/03/the-bailey-borwein-plouffe-algorithm-in-c-and-f/#comment-4415
http://bitbiz.io/threads/altcoin-taucoin-new-arm-excusive-coin.142/
The reason to calculate Pi in with the methods described in the OP is useful for checking if the second attached link really is doing what it is suppose to. Which is calculate a given place in Pi without having to calculate the preceding numbers.
All of this is useful for the first link that I’ve posted which aims to “compress” files by addressing parts of it’s data into sections of Pi. Which is really cool as the method used to derive your first address list can be further compressed again before storing or sending to a remote server for reconstruction.
I plan to use these methods in the third link that I posted where I’m also combining Crypto currencies and MPI for ARM CPUs. Which also will work on RPi’s and micro controllers.
So Pi may be round but it is not without it’s points.
Hmm. Well, I’d heard long ago that you could could create a circle around the visible universe with an error of less than the width of a proton with only X digits of pi, but when I googled, it, I found X = 32, 39, 41, 43, 47, and 50. Well, a bit less than 10 trillion anyway. :}
Strangely, no 42 :)
I actually did this once myself, except it was the volume of the Universe in Planck volumes. I came up with about 300 digits.
Some people keep trying to see if there’s a point where pi stops being irrational. :)
Come on, everybody know that supercomputers can’t cure cancer. Only pink ribbons can.
I got pi by doing something like 1\log2 or something… wish I could remember what I did.
i remember deducing it as the limit of some equation of the radio of a polygon with the number of faces going to +inf.
it was just a matter of putting like 10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 faces and you get a lot of accuracy in the result
Only 7.3 trillion more digits until it repeats, keep going!
“Only 7.3 trillion more digits until it repeats, keep going!”
Really???? Prove it!
any one else think this could have been SOOOO much faster with a set of nvidia teslas? XD
Oh Goody!..now i can finally calibrate my new modified Q-32 Space Modulator…and when i’m ready to use it, it will make a great big KABOOM!
I know all the digits of Pi.
Unfortunately, not in order.
Rainman would have been proud.
errr uhm , pi is wrong :P
http://tauday.com/
yep it was a pointless self gratification exercise
Knowing more digits of an irrational or a larger prime number A) give you bragging rights B) let you encode/crack more difficult encryption schemes.
I remember reading an awesome article on the Chudnovsky brothers (think the newyorker linked on wikipedia), it sounded as if their whole house was given over to a supercomputer, it also outlined their various hardships. It would be nice to see an update.
I actually have access to a top 500 computer for supersonic flow analysis, I might be tempted to give this a go. I’m not sure if I should say exactly what computer but I will say it’s got over 1500 xeon 5660 processors and near 20 TB of ram
I have followed Alexander Yee’s work for awhile, and there are some very good reasons that GPUs are not ideal for calculating pi. I think the main reason is memory bandwidth–when you’re multiplying very long numbers, you’re constantly having to go to RAM, and this is far from speedy with current GPUs. Clustering has similar issues, but the main issue with clusters I think is effective multithreading. Alex discusses that too at his website.
The reason for calculation the end of the PI is simple. It is required in order to ‘calculate’ an accurate simulation of our beloved reality.
PI CANNOT BE A SQUARE FOR PI’S ARE ROUND; COBBLERS ARE SQUARE!