As an HVAC engineer by trade, [Carlos Paris] spends a lot of time in AutoCAD designing all those hidden pipes, tubes, and ducts hidden in a building’s rafters. One day, [Carlos] read of an open contest – the prize was over a million dollars – to generate a prime number with a billion digits. [Carlos] misheard this as, ‘a prime number greater than one billion’ and of course said this was a trivially easy task and opened up his favorite tool – AutoCAD – in an effort to discover the largest prime ever. [Carlos] never generated a remarkably large prime, but he did come up with a very, very cool visualization of prime numbers on a number line, as well as a great justification of the twin prime conjecture, a problem in mathematics that has remained unsolved for several generations.
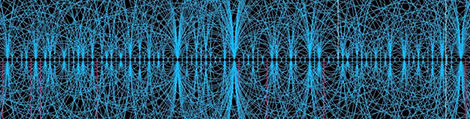
[Carlos] started his investigations into the properties of prime numbers by drawing a series of circles on a number line in AutoCAD. These circles were of diameters of all the integers, and going down the number line, these circles started to have an interesting, chaotic pattern (see above picture). [Carlos] found that whenever two circles intersected, that position was a prime number. It’s really nothing more than a Sieve of Eratosthenes, but it’s a very cool-looking visualization nonetheless.
Looking deeper into his graph, [Carlos] discovered there were certain primes that had another prime number just two places down the number line. For example, the numbers 3 and 5, 29 and 31, and 41,and 43 are twin primes, as the difference between the primes is only 2. The idea there are infinitely many twin primes is a famous unsolved problem in mathematics – it’s obvious it must be true, but no mathematician has yet come up with a proof of this conjecture.
[Carlos] looked at his number line and simplified it to a generic prime number. By taking a generic number line and overlaying the multiples of other prime numbers on this graph, [Carlos] had a very, very clever way of understanding exactly how twin primes come into existence.
In the end, [Carlos] is no closer to proving the twin prime conjecture than anyone else. We’ve got to hand it to him, though, for nerding out with an engineer’s favorite tool – AutoCAD – and managing to derive some fairly obscure mathematics on his own.
After the break you can see [Carlos]’s videos describing the though process that went into his creation. Very, very cool work.
[youtube=http://www.youtube.com/watch?v=UYkLz8BIS8k&w=470]
[youtube=http://www.youtube.com/watch?v=BXksbyWyp-4&w=470]
[youtube=http://www.youtube.com/watch?v=J-UcdY3lZRk&w=470]
[youtube=http://www.youtube.com/watch?v=1K2vHiqQpV0&w=470]















HaD: uMaD?
(Math a day)
It’s great when something like this filters through (even though in this case it was mainly because of the pretty picture and AutoCAD).
The best hacks all seem to involve some amount of math and hard work. Without those two ingredients, all you have left is piddling around with an Arduino and copy-pasting in someone else’s code.
Although I am pretty sure you can use an Arduino to check Mersenne numbers… Okay, maybe not.
I’d call it a hack. I don’t think the designers of AutoCAD ever sought out to build a prime number generator.
in the words of Inigo Montoya – “You keep using that word. I don’t think it means what you think it means.”
You are absolutely right we at Autodesk never expected this to be done in AutoCAD and customers are always blowing our minds with how they use our products and technologies far beyond our expected use cases.
http://bit.ly/SMw344
Huge CAD Geek kudos to Carlos Paris!
Shaan Hurley
Autodesk, Inc.
Definitely a cool visual representation, but if i remember rightly the actual proof will probably fall down to someone who is a ‘pure mathematician’ or at least studied that at university, which will usually preclude them to being able to relate to the rest of the human race so well. Go Carlos …
If someone really wants to impress me, do it in excel …
=ISPRIME(A1:A65536)
wut?
More story like this, please!
There was effort put into the introduction that your average HAD post too.
Also, I don’t dig math much, but for all our sake I think a math topic from time to time could be a good thing.(for example, someone mentionned mersenne algorithm. how about math behind pseudo-random generator?)
Putting the “abstract” (math concepts) into a visual representation (more concrete) helps many people to see the relationship between numbers (abstract) and counting actual objects.
This reminds me of “The Binomial Cube”
http://www.infomontessori.com/sensorial/visual-sense-binomial-cube.htm
or “The Trinomial Cube”
http://www.infomontessori.com/sensorial/visual-sense-trinomial-cube.htm
> The idea there are infinitely many twin primes is a famous unsolved problem in mathematics – it’s obvious it must be true…
It’s not obvious to me. Is there a reason it should be obvious?
Of course it’s obvious. There are an infinite number of primes. Even if only a small percentage of them are twin primes, there’s still an infinite number of twin primes. Unfortunately, it’s one of those impossible to test problems, as there are always more numbers to test.
Perhaps “obvious” is not the right word, more like “apparently” – appears to be.
Sometimes an excellent fail is almost as good as a win. +1 Carlos, very well done.
I’m no mathematician, just a lowly engineer…but starting with the prime 3…if you add 1 to it, it will be even thus not a prime. If you add two it will not be divisible by 3. Same with 5 and 7…however it you add 2 to the second prime of te pair (7) it will be nine, thus be divisible by three. Same with 11 and 13 – add two to 13 and you get another number divisible by 3…i suppose while this seems to be obvious that it must exist for every first prime of the twins, and probably exists for every new prime discovered, its difficult to come up with a mathematical proof of it.
Much simpler proof: Take a series of primes. Multiply them all together. Add one. The factors of that number will not be in your list.
That doesn’t guarantee the result is prime, but it has more primes than what you started with.
Oh, wait, misread as proof for infinite primes, not twin primes. Sorry.
great article thanks, cool to use a programm out of specs like that!
…I look at the image and for me it reminds of the work done by Alex Grey (/w Tool). Some of the works that evolved from the ‘Net of Being’ are quite similar.
Has anyone else noticed that the first pic tends to appear to have depth to it even though it appears to be a 2D line?
This video I made definitely shows an odd 3d effect when fastforwarding the sieve up to 20.000:
http://www.youtube.com/watch?v=7wFjieSZQdU
I just have to try that illustration in Inkscape, but unfortunately I have never programmed in Inkscape so I would have to do it by hand.
At the other hand Context Free should be the perfect tool for this.
This was one of the more awesome things I have seen. Rock on.
> …an engineer’s favorite tool – AutoCAD
…is akin to an addict’s favorite drug – Heroin!
Its the ONLY tool and Autodesk is the drug cartel who has eliminated or absorbed through financial force all competing cartels…
fuck autodesk with a brick.
Ha ha, sounds like Carlos needs to consider taking on more challenging projects at work….
P.S. If visualizing mathematical concepts with drafting software isn’t considered a hack, then I am a rich engineer…
So, this is the source of all this crazy traffic! I’m extremely happy like-minded people like you guys have seen this. Doing this was one of the most mind blowing/expanding experiences ever, and sharing it with the world has been a lot of fun and very interesting. AussiTech commented sometimes it takes an excellent fail to make a win… Thank you! and thank you too Hack a Day!!
Carlos Paris has, in my opinion, used the tools at hand to explore and explain what he found. Kudos for your effort. This is the stuff of invention, of consideration, of exploration, of being more than a bump on a log or someone who has nothing to do but put other people down. Maybe be he didn’t win this time but who knows what the future will bring. keep an open mind Carlos and don’t give up.
Your friend
Bob
Anyone else notice that the sieve in the first vid @ ~ 12:27 looks like a waveform.. I would love to hear what that sounds like…
You had the right idea. A circle is not quite the curvature you need to describe the integers or primes landscape. You overshot. Why? A circle’s curvature is too much.
In reading the corrective and adaptic optics for Hubble this idea occured to me:
Your circle will produce ‘aberration’ in the landscape of integers. With ellipses as units you will find much more than with circles – without invoking probability or ratios.
What curvature to produce any prime I do not know. I only know finding any prime is one of curvature.
All the best.
Think of curvature also as a compass. The right curvature will point to any prime.
You have to experiment. The ellipses don’t have to be vertical to the horizontal axis when tangentially touching. The same scheme however as for circles.