If you’re reading a thermocouple with one of those fancy schmancy SPI thermocouple amplifiers, this one isn’t for you. If, however, you’re still going through those old-school analog thermocouple amplifiers like the AD595, [miceuz] has just the thing for you. He’s come up with a library for embedded devices that reads the temperature of a k-type thermocouple with +- 0.03°C of accuracy.
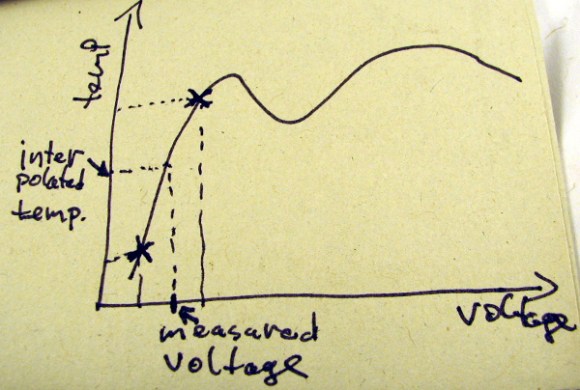
As with anything dealing with natural phenomena, the voltage generate by the bimetallic junction of a thermocouple probe is decidedly non-linear. This is a problem when dealing with embedded devices, as that would mean using floating point arithmetic, greatly increasing the amount of code. [micuez] found the NIST tables for a K-type thermocouple and interpolates the actual temperature of the thermocouple probe from the NIST data. The usual way of measuring thermocouples – a polynomial unction of some sort – has an error of about 0.06°C. [miceuz]’s library has an error of less than half that, all while using less code.
The library doesn’t support temperatures below zero, but this is still a work in progress. Still, if you’re looking for a very accurate library for a forge, crock pot sous vide build, or a toaster oven reflow controller, you can’t do better than [miceuz]’s work.















The library converts K thermocouple voltage to temperature within +/- 0.03°C, actually measuring temperature with that accuracy is quite another thing. How much noise/error due to the amplifier? How much due to the ADC? How much due to the cold junction compensation? Also placement of the sensor and ensuring good thermal contact is very important. In real life, anything higher than +/- 0.1°C is very hard to get and in many cases meaningless.
Not to mention that impurities and construction means that your thermocouple is unlikely to perfectly match the standard curve anyway.
If you’re after that kind of accuracy, if you’re after anything beyond +/- 0.5C then you’re better off using an RTD anyway. They are far simpler devices to read, and assuming you have all your own influences sorted out they are also more accurately manufactured.
RTD is a bit easier on the hardware side, but still requires some form of linearization.
BTW Analog Devices has a good app note AN-709. They also have a table generator (for that app note) for piecewise approximation based on the temperature range and table size you want.
+/- 1 °C is already hard to get, and requires careful calibration. With typical uncalibrated thermocouples, consider yourself lucky with 2°C error. Still, the conversion errors are added to the measurement errors, so if you can get 0.03 with minimal fuss, it’s still a good deal.
Great post! This will certainly come in handy
My current project is a reflow oven and I’m intending to use a MSP430AFE as a single chip amplifier and controller. I’ll let you know if it works (or of it’s a “fail of the week”).
I was going to use the standard lookup table with linear interpolation technique and was quite excited to see another option. It seems this IS a lookup table with linear interpolation. Odd that he couldn’t find any examples. It is certainly well documented, although it’s not clear what it’s better than – i.e. what code produced the 0.06C error.
Agree with the contents above that if you think you’re getting better than 0.5C then it’s probably:
a) accurate enough
b) not as accurate as you think it is
The 0.06 error comes from here: http://srdata.nist.gov/its90/download/type_k.tab
Scroll to the bottom of the page, where you’ll see three polynomials for different temperature ranges, with a maximum error of 0.06 degrees. These are the inverse functions from mV -> temperature. The forward functions are listed slightly higher, and they are considered the reference.
Thank you.
This is part of the NIST ITS-90 thermocouple database that you can find here:
http://srdata.nist.gov/its90/main/
(probably a good link to include in the article summary)
Where/what you measured can contribute much more error than the uncorrected thermal couple. Are you taping it down to the PCB near the more difficult parts or just like leave it hanging in the air?
There are reflow machines with multiple temperature control zones to give better control to areas in a board with different density/component reflow needs.
Well, yes, the method is well documented, I’m not telling I’ve invented it :). Just all the freely available TC compensation/linearisation code I could find was using polynomials and floating point.
I totally agree that 1°C accuracy is very hard to achieve, but there is no point to piss ir away in software when you can easity avoid it.
Another interesting way to do linearisation is to use the forward polynomials (temp -> mV) and use Newton-Raphson method to reverse them. To reduce the number of iterations, you can take the last conversion result as a starting point. If the temperature swings are slow, a single iteration may be sufficient. This is also a nice method to do for simple and accurate Pt100 RTD conversion.
When using a thermocouple, you must also measure the temperature at the junction (where the TC is attached to copper traces, basically) and compensate. Often, a diode or thermistor is used, but you could use a modern dedicated temp sensor. Calibration is pretty important, for both the thermocouple AND the junction.
This means that to get decent accuracy (as opposed to resolution) you probably need to have access to a high quality temp sensor. You can use the triple point of ice water for zero, but getting a higher temp reference point is harder. You can use a salt or sand bath, as long as you stay below the breakdown temps. Basically, you need a crockpot full of salt.
That gives you two points. Once you get much past 400F it gets trickier to calibrate. BTW, you can cobble up thermocouples by pretty much twisting together almost any two kinds of wire, for example aluminum and copper. Hint – guitar strings.
Okay-OLD Instrument engineer coming through-thanks for the space…
0.03DegC resolution is doable, but with an accuracy of +-2C is the penalty, so I agree with earlier posters.
This said, remember that thermocouples don’t measure temperature-but TEMPERATURE DIFFERENCE between the thermocouple and the cold junction (also a thermocouple, BTW) and a third-party device must be used (RTD, thermisistor, thermostatically-controlled oven (an isothermal block) is the usual suspects for doing so. In most applications the cold junction is usually at room temperature, so as long as you are significantly above or below 25C you’re good.
What thermocouples suck at is measuring temperatures close to their cold junction temperature. I had to carefully explain this to a Lab Scientist one day that his temperature monitoring rig (located in a very tightly-controlled lab (25C, +-0.5C) was useless because the sensors and the monitor were in the same room-so of course they always showed 25C!
The code is just a linear interpolation over a “hand-picked lookup table”. The interesting bit would have been how that table was picked and why it outperforms polynomial interpolation because that bit isn’t clear, to me at least.
The points in the table were picked at the most nonlinear parts so that max error goes down
How about using an RTD with a low cost 4-20 mA current loop transmiter http://s.click.aliexpress.com/e/QNVNnYf with a precision resistor ( Usually 250 Ohm )