If there’s one thing that a lot of small microcontrollers hate (and that includes the AVR-based Arduini), it’s floating-point numbers. And if there’s another thing they hate it’s division. For instance, dividing 72.3 by 12.9 on an Arduino UNO takes around 32 microseconds and 500 bytes, while dividing 72 by 13 takes 14 microseconds and 86 bytes. Multiplying 72 by 12 takes a bit under 2.2 microseconds. So roughly speaking, dividing floats is twice as slow as dividing (16-bit) integers, and dividing at all is five to seven times slower than multiplying.
There’s a whole lot of the time that you just don’t care about speed. For instance, if you’re doing a calculation that only runs infrequently, it doesn’t matter if you’re using floats or slow division routines. But if you ever find yourself in a tight loop that’s using floating-point math and/or doing division, and you need to get a bit more speed, I’ve got some tips for you.
Some of these tips (in particular the integer division tricks at the end) are arcane wizardry — only to be used when the situation really calls for it. But if you’re doing the same calculations repeatedly, you can often gain a lot just by giving the microcontroller numbers in the format it natively understands. Have a little sympathy for the poor little silicon beasties trapped inside!
Float Avoidance
You can often completely avoid floating point numbers just by thinking a little bit. Simply seeing a number with a decimal place is no reason to pull out the floats. For instance, if you have a quantity, like the temperature on an LM75-style temperature sensor, that’s accurate down to 1/8 of a degree, you absolutely positively don’t need floating point numbers. How can you deal with 21.125 degrees without floats? Exactly the same way the LM75 does — it pre-multiplies everything by 8.
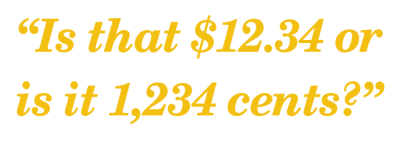Avoiding floating point numbers is often as easy as figuring out what the natural units of the problem are. Is that $12.34 or is it 1,234 cents? I can only cut with a hand saw accurately to about a millimeter. If I measure board lengths in millimeters, I’ll never need a decimal point. Sure, the numbers get bigger, which means that you may need to use the next-largest integer storage size, but microcontrollers don’t mind that nearly as much as floating point math.
So if you’re taking a reading from a 10-bit ADC, and it’s range is 3.3V, the last thing you want to do is convert that directly to volts after measurement (even though it might make your code read nicer.) Keep the ADC value around — it’s a nice 10-bit integer — and only convert out to actual volts when you absolutely need to, after all the other math has been done. And when you do, note that the right units for your problem are in terms of the minimum-possible measured difference, which is 3.3 V / 1023 = 3.23 millivolts. When you need to convert to physical units for the end-user, you’ll multiply by this value.
Try redefining units of measurement any time you’re running into fractions or floating point numbers. You’ll be surprised how often you didn’t need them in the first place. There’s one warning here though: be careful when converting back to the desired units. A square centimeter isn’t 10 square millimeters, it’s 100. Each “millimeter” in the conversion brings a power of ten with it. And ten millimeters divided by one millimeter is just ten, with no units left, and no need for conversion.
Fixed-Point Math
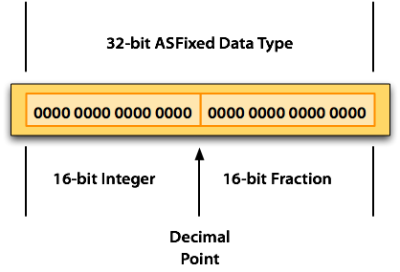
While simply getting away from the slower float type can be enough of a speedup for some cases, there’s an extra layer of optimization available, should you need it. A common choice, for instance, on small microcontrollers is to simply multiply all values by 256. This is called “8:8 fixed point” notation, because you’re using eight bits for the fractional part, and eight for the integer part.
It turns out that if you know the number of bits in the fractional part, you can optimize multiplications and divisions to run even faster than a 16-bit multiplication or division. Here’s a nice writeup of fixed-point math options for the Arduino, for instance. You can read up on a bunch of these optimizations in this Atmel application note. And note that the algorithms aren’t specific to any platform.
So when you don’t need arbitrary fractions, fixed-point libraries can be a real speedup over using floating-point routines.
Floating Point Numbers Are Lousy Anyway
There’s a fairly well-known problem with floating point numbers: you have to be very careful when testing them for equality. That’s because they’re all not represented exactly. For instance, 0.1 isn’t representable exactly in floating point, so if you add ten of them up, it’s not going to be exactly 1.0 either. If you were to test sum10(0.1) == 1.0 it would end up false. That’s lousy.
The other thing that’s peculiar about floating point numbers is due to the way they’re constructed. Floating point numbers are like scientific notation (1.23 x 103) except in binary. IEEE 754, which most compilers follow, uses 24 bits for the first number — the number of significant digits — and 7 bits for the exponent. This lets you represent both really large and really small numbers. But because there is the same number of significant digits everywhere, the gaps between representable numbers is very small for small numbers and doubles with each power of two in the exponent.
For example, 123456789.0 + 1.0 == 123456789.0 will be true because the spacing between the 24 bits of significant digits is larger than 1. 123456789 + 1 == 123456789 will be false if you use integers, because the spacing between integers is always one exactly.
In short, integers are exact, and they keep the same distance between representable values throughout their range. I find this often corresponds very nicely to the kind of inputs and outputs I use with microcontroller projects. Floating point numbers, on the other hand, have a much wider range, but do so at the expense of growing distances between possible values. And when floats can’t represent numbers exactly, comparisons are not going to work exactly.
Joyless Division
Most of the lower-end microcontrollers (again, including the AVRs used in the Arduino) don’t have hardware division built in. This means that they will be using some kind of iterative algorithm to find the answer. This takes a while. There is a great shortcut, at least for integers, that you should know about. In binary, dividing by n powers of two is the same as dropping the least-significant n bits off the number. x >> 2 bit-shifts x over by two places, effectively dividing by four. It’s just like dividing by ten in base-10. Drop the last digit.
This type of bit-shift division (and its dual, multiplication) is optimized in for you by AVR-GCC, so you don’t actually have to think about it. But it ends up with the odd situation that x/4 runs extremely quickly, while x/5 can take a bit longer. If you can pick your divisors, you should always pick them to be powers of two. If you were going to average ten values together, your algorithm will run a lot faster if you only use eight observations, and may not be all that much worse if you use sixteen.
Integer Division Tricks
Which brings us finally to the promised dark wizardry — two nasty tricks that you can use when you need to divide integers in a hurry. The major caveat is that these techniques only work when the divisor is constant. You have to know what it is ahead of time to use this. But when you need to divide by thirteen over and over again, here’s two ways to get you there as quickly as possible.
Multiply then Divide
The basic idea here is to pre-compute your division as a multiplication and a bit-shift. In the same way that you could divide by two by first multiplying by five and then dropping the least-significant digit (effectively dividing by ten), you can pre-compute the binary multiplier and number of bits to drop. The idea was laid out in this post by Douglas Jones, and then coded up here.
In particular, to divide any 8-bit number by thirteen, you first multiply the number by 158 (resulting in a 16-bit integer) and then drop the least-significant eleven bits. Yeah, right? It works because 158/211 ~= 1/13. It’s just math and it’s going to run about as fast as possible, but it’s not entirely readable.
Lookup Table
If you really, absolutely need to divide by thirteen in a hurry, there’s one way that’s faster than the above trick: pre-computing all the possible values beforehand and storing them in an array. For instance, with 8-bit numbers, create a table of all possible 256 values divided by thirteen. We’ll call it thirteen_table[]. Then when you need to know what 123 / 13 is super quickly, just look up thirteen_table[123] and you’re done. It’s cheating, and it uses 256 bytes of memory, but if this trick gets you out of a sticky situation, it’s worth knowing.
Premature Optimization
There’s a maxim of Donald Knuth’s, “premature optimization is the root of all evil“. The basic argument is that if you always write your division routines aiming for maximum speed, you might end up with an unreadable mess of code for very little benefit. Maybe the right place to spend your optimization time was making sure that two different subsystems could run concurrently, or something else.
So take all of the above with a grain of salt. Thinking your units through, and figuring out if it’s possible to re-cast them into integers, is probably always a good idea if you don’t have hardware floating-point math. Swapping up arbitrary divisors for a power of two is also pretty much always a win, if you’re already using integers.
Whether you want to take the next step to a fixed-point library, or are able to use the dirty tricks for fast division by constants, depends on your situation and your needs. If it over-complicates your code and the CPU has lots of free time, or if it’s in a non-time-critical section, don’t bother.
What other dirty math tricks should we know about? What’s your favorite or most-hated? Integer vs. floating point? Let us know in the comments!
“If you were to test sum10(0.1) == 1.0 it would end up false. That’s lousy.”
Floating point is not lousy. You are. (your expectation of it anyway). Since when did nonassociative addition ever equal lousy? It’s just a mathematical operation. Floating point equality works fine when you understand exactly what you are testing.
rant
Oh my gawd a ‘Rev’ – what is that on a tech site ? sorry but you have missed the point totally and oh so facilile, see my last post please, why the title “Rev” here anyway, are titles so damn important to your sense of self, is this a misplaced “Appeal to Authority”, that went out > 150yrs ago ? its not congruent with Science or Engineering, its meant for the age of religious claim re status, authority and power over the intellectual feeble – not here and setting oneself up as “closer to god than the common man” eek, from primitive times when people thought god sent lightning – we’ve done it, its Electrical Engineering really ?
/rant
Get a grip, no tech in any bible versions I know of cept Hinduism & vedas re rate at which universe ‘flickers’…
PS. Hope I am wrong an “Rev’ is a nick not a religious title, if former apologies if latter, middle east for you ;-)
Better go to your sage place.
Ha! Nice mistype destroys barb :-) Safe place.
Why don’t you simply read his words instead of engaging in ad hominem garbabe? While not a believer myself, plenty of adherents to a variety of faiths have made great contributions to a vast range of technical fields: think Stirling engine; think Baye’s theorem; think Mendelian inheritance; and that’s just Christians. Unless someone telling you what to do, keep your views about their personal beliefs to yourself.
That is completely disingenuous. IEEE Floating point math is confusing. There’s tons of traps, holes, and misunderstandings all about in it.
First you have to keep these rules in mind: https://en.wikipedia.org/wiki/IEEE_floating_point
Next you also have to keep track how your C compiler interprets these rules.
Finally, you have to understand the effects and side-effects of using floats in your code.
I’ve seen more errors on the “edge cases”…. and there’s tons of edge cases. I’ve seen professional electronic engineers pare through the levels of documentation to understand why a float isn’t doing what it should. I’ve seen CS graduates mess up float calls and have cascading errors in a matrix.
So yes, you can insult, but can you actually do it? I know I stick with ints when I can. I know when I’m out of my league.
Fixed point would have trumped floating point long ago in the dark ages, but go ahead and define a SINGLE standard of data interchange using fixed point. You can’t.
Second, please regale us with tales of the edge cases…denormalized numbers (hardly ever come up and easily dealt with)? Infinity? (representing Infinity is an asset, not a drawback). NaN? (also an asset, not a drawback).
Anti-floating point groupthink is as productive as flaming FTDI.
I work for the world’s largest bank. My group processes several TeraBytes of data a day, most of it in numerical format. We use fixed-point math because we CANT have errors in our calculations. ALL of our data interchange standards require fixed precision instead of float-point.
Even more important than my work is that of the EEs who develop critical infrastructure and have to rely on shytty floating point stuff. Remember that US military base that got hit with a missile because their missile defense system had a float-point error?
We are talking about embedded systems running on 8bit micros. If you are using an ARM with an FPU then using floating point is not a real big issue. On a PC it is not a big issue at all. On a small embedded system it is an issue so fixed point does have some value.
As far as a standard format for fixed point that is also not an issue. You would always convert your fixed point data to floating point before you export it from your environment to outside system. That may mean changing it to floating point or even a string before writing it to an SD card or sending it over TCP/IP or serial port or having a communications program running on a PC do the conversion before sending the data off to outside systems.
Even BCD has value in some tasks so you should not be so dismissive of these methods.
“Anti-floating point groupthink”
Rejecting floating point due to it’s complexity in a scenario where you’re already limited in processing capability and program memory isn’t “groupthink” it’s “engineering”.
Quite frankly floating point belongs on a microcontroller ONLY in edge cases.
How about this, climate models generate different results when run on different architectures. http://journals.ametsoc.org/doi/abs/10.1175/MWR-D-12-00352.1
jwcrawley, there may be many traps, but the first damn rule of floating point is “Never test equality of two floating point numbers.”
I think that the article is trying to make a more subtle point: just because you write 0.1 doesn’t mean that the computer is actually computing using 0.1 exactly due to the underlaying binary representation. That IS an important point, but using an equivalence test with a pair of floats to make the point buried the lead under a glaring piece of bad practice.
Just as with floating vs fixed point, representation matters…
But that’s my point as well.
On the surface, it’s obvious that you don’t compare a float with a number. But how many other of these side-effects occur everywhere when using floats? That’s the crux of the problem: the surface area of side effects are huge.
If you have to use floats, cool. Understand them, and how they are used and how they fail at the edges. They can be great to use when doing things like Haar cascades, neural network weights, and such.
But most problems can be reduced to that of integer representation.
Gosh, if you can’t even test equality of two numbers, those are lousy numbers. Even a child can compare two numbers written on a sheet of paper.
Why are so many internet-engineers unable to comprehend subjective words like “lousy?” If you only like narrowly defined, objective words you should still be able to compare a word to that and find out that it is a subjective word, and then you would know to prefer a different word instead of arguing with it.
The funny part is that the argument people are making that “that’s just part of it means to have a floating point number” is the same thing that refutes them, when applied to the words being used: that it is opinion is part of the meaning of the word “lousy!”
You would never use a comparator to test if two analog signals were equal to each other. You would use a comparator to test if they were equal to each other to within some tolerance (i.e., use a window comparator). The same goes for floats.
You should never write if(myvar == 3.0){…}. You should instead write if(myvar > 3.0-a && myvar < 3.0+a){…}, or something similar, where 'a' defines the range on which you have decided that something is close enough to 3.0 to be considered equal to 3.0 – but there's that word "considered…"
They are not intended to represent exact quantities. They are intended to represent quantities with a given precision (hence why Elliot's comparison to scientific notation is SPOT ON). Anyone who looks at the number 1.234 x 10^3 should immediately recognize that the last digit of the mantissa actually is a stand-in for something in the range [0.0035 x 10^3,0.0045 x 10^3), unless it is stated somewhere that the number is an exact representation. When I have two numbers with x digits of significance and I multiply them, the result will have 2x digits of significance (not necessarily accurate to that many digits, but that many digits can be calculated exactly). However, unless I use a variable precision variable type, the result likely is going to have the mantissa truncated and rounded. Right there, you've implicitly accepted that the result is an approximation. All I need to care about is that the computational hardware does the computation and truncating/rounding for me in a consistent, predictable way.
From a computer as a machine point of view, of course you CAN compare two floats, but you never SHOULD, because the comparison makes little to no sense outside of a handful of cases (and if you ever actually encounter one of these cases, I can pretty much guarantee that you'll be so comfortable with the nature of floating point representation that you'll know what you're doing). Floating point numbers are wonderful, but only if used properly.
I don’t think most people really know how float do work under the hood and expect that comparisson to be true. That is lousy indeed and that is what he is saying. It is just plain stupid that ten times 0.1 isn’t 1.0 (Yes I understand why it isn’t exact 1.0 :))
should be an reply to Rev Tactule btw
You have limited sight. If human dealt in binary and computer performed decimal you’d have the same situation. This expectation is just radix bigotry.
Speaking of which, C using upper and lower case letters interchangeably in hexadecimal is radix numbskullism. Some systems use RAD60 or higher and upper is a different ASCII value from lower. I pine for the days when 7af6 was an error in radix 16 and conversion used a 16 entry lookup table. I can still barely read C library code without grinding my teeth. I have an urge to “fix” all the hex numbers. Then remove the redundant white space. Then put the simple if-else statements on single lines. then…..
Pre-processor really needs a HEX and BINARY and DECIMAL mode, much as modes can be a problem, and get rid of this 0x nonsense when filling in tables or doing headers all in hex addresses or register masks. People have used it so much they actually write hex numbers in text with a 0x attached.
No where were we?
“If human dealt in binary…” Then we would never think of “0.1” as a number. We don’t deal in binary and we routinely use that number. If we made computers that had intrinsically decimal representations (or taught our children in intrinsically binary representations), we wouldn’t have this sort of conflict. It’s nice to argue in hypothetical spaces, but they have no relevance to how computers and people actually work in the real world.
And you can’t read… The world is seen through analogue eyes..
The statement in this post is 10 times 0.1 equals to 0.1 and NOT 10 times 0.1 equal-ish to 0.1.. That is confusing (and even if you understand the rules as jwcrawley says and it would take a lot off extra code to circumvent the shortcomings of this example and make it work (and more complex code in real life))
But on the other side your DVM says 12.00V to 12-ish Volts, and we all accept this equals to 12 volts..
“radix bigotry”… i love that phrase :)
It’s worse! Ten times 0.1 _is_ 1.0. It’s adding ten 0.1s together that doesn’t give you 1.0.
Maybe instead of “lousy” I should have said “much trickier than most people think, and this ignorace can bite you in the ass” or something. But I think that’s lousy, personally.
Floating point numbers can make transitive computations intransitive. Sometimes. Most of the time, they don’t. I’ve done enough numerical work in C to know where the traps are, but I’ll be damned if I’d want to do a code review to go looking for them, and I’m sure I’ve made many mistakes.
Integers: ok to add a big number to a small number
Floats: danger!
But what if you don’t know, a priori, the relative size of the numbers?
If you left your article discussing fixed point and integer tricks it would be great. But you got out of your element with floating point.
And from what you just said about integers, overflow is an OK condition for you? You check the overflow flag in your assembler?
If you do not know the relative size of your numbers fixed point won’t help you either.
Are you just a troll? Seriously. The rest of us got the point.
Do you really need to ask? Seriously…?
If you left your cave and actually did some coding you’d know how bad floating point numbers are and how easy the article is being on them.
Too bad you weren’t on that military base that got blown up because of a floating point error!
…that got out of hand a little fast–
Yes, checking for overflow is generally considered good.
And indeed, if I don’t know the relative size of the numbers, and they overflow, I can just check that easily. I’ll never have a mathematically incorrect answer with no flag to check.
All I need to know for fixed point is the format. And in C, I need to know that anyways, so it is no loss. On a microcontroller, I better already be obsessing over knowing how many bytes everything is. And on a full size CPU, I can always just use a library like dec_number (IBM has an implementation I like) that will give me mathematically-correct results and can accept varying inputs where I don’t actually need to know the exact format of each.
How can a person hope to program a microcontroller if checking an overflow flag is a bad thing?
Re: Overflow.
IEEE’s float overflow behavior is nice when you’re doing math. I’ve made my peace with “infinity” as a result for multiplying two big numbers. You’d almost never overflow a float on purpose, so it’s as good as any other compromise.
Overflow in (unsigned) integers is useful as a quick modulo, though. Granted, unchecked integer-overflow is a horrible trap for people who aren’t used to it, but I actually like the flexibility. And that’s one of the things you learn in your first semester of C anyway, right?
The larger point is that Floats have a very specific purpose, real world analog values. Floats are not numbers, they are approximations of a real value. Adding ten exact 0.1s would give you exactly 1.0. But that’s not what you are doing with floats, you are adding ten approximate representations of the real world value 0.1, which would give you approximately the real world value 1.0. Adding a small number to a vary large number gives you approximately the same number. 1mm + 1km = 1km. No danger here, it’s by design.
Saying floats are lousy is like saying hammers make lousy screwdrivers. While true, you are simply using the wrong tool for the job. They were designed for scientific calculations, so unless that’s what you are doing you should be using fixed point numbers.
Microcontroller ADC and DAC output is integer. If you need to display the number, chances is that there are limited number of digits which can be represent in integers.
A 32-bit representation in most cases have large enough dynamic range. You can count from uV to 2kV. Is that not enough? A 32-bit float actually has less precision for the same range as they use some of the bits to store the exponent.
Well no, they’re still lousy. There are instances where you’re you have no choice but to deal with floats (say as geometrical coordinates) and you’d really like them to be “exact” when possible but they just aren’t – dividing a 1.0 long segment into 10 individual sections then computing the length of the chain will not get you back to 1.0, but most people will forget that at least sometimes. And don’t even get me started on what happens once you involve arcs and angles, exactly 360 degree spans and all the rest – hint: you WILL screw it up. Repeatedly.
Damn good posting and absolutely spot on in so many ways, well done :-))
Circa 1980 had consultancy contract with Pretron Electronics in Perth, Western Australia, they designed a nucleonic ore flow gauge for Mt Newman Mining. Used Cs137 beta emitters as a pair to determine mass flow rate of iron ore across various mesh screen particulate separators by relative absorbance/transmittance – all driven from software reading the electron beam counts from a pair of scintillation counters by the newest 16 bit micro, an NSC Pace-16 which ran a low end Forth like stack maths at assembler level – everything suggested by Elliot Williams is absolutely spot on re my experience decades ago, as to; minimise cycle time & cumulative roundoff error – the output went to a chart record for audit purpose and also to a Foxboro r Honeywell servo controller to modulate the angle on the ore flow feed gate so the screens wouldn’t clog having the site workers (complain about the engineers) jump in with shovels to clear the dross, what a brilliant piece of leading edge microcontroller work for the time – much qudos to Dave Gibson for the initial design layout late 1970’s and Indesa Rajasingham for the Kalman filter rate of change real-time analysis which I initially coded in assembler/forth whilst giving Indesa a leg up on micros as his area was sampled data systems control stability criteria, it was great fun overall with a few site visits to Mt Newman & Port Hedland in the mining region of north Western Australia :-)
Then some 4 years later took over management of Pretron’s press brake CNC division and used the same “flow integer” techniques along Elliot Williams line, ie deferring formating as long as possible for efficiency – first on a Z80A, then an NSC800 for determining the hydraulic tool penetration depth according to input from a metal sheet worker vs die sizes for precise bends on range of materials on hydraulic press brakes from 40T to 500Tonne capacity for Queensland Locomotives ie. The controller had to decide penetration in 0.1mm steps for angles from 179 to 70 degs or so and work out the bend allowance too from drawings as well as compensation for machine flexure whilst bending things like 9m long tapered hex lamp posts 1.6mm galvanised to 1m long 2″ thick layered steel casings for the local military base bomb-case test structures, ie All great fun and leading edge of the time.
This article is absolutely spot on, we don’t need to waste CPU time or ram to fiddle with internal representation re units/decimals, we just need to pin down optimum data flow and then only minimally concern ourselves with display (later) when its really necessary and then when on a 7-segment display where time is not of the essence – heck the metal workers hardly check the readouts making all sorts of dumb assumptions, limb risk included !
Thanks a heap Elliot Williams, you took me right back :-)
Those lessons have served me well in all sorts of diverse ways and not just directly but spilled over into other areas I never expected that such consideration re optimisation essentials would ever reach, cheers and well done for a most refreshing, interesting and thought provoking article which sadly is unlikely to be understand by most contemporary run of the mill (industry) microcontroller programmers fed the highest comparative caviar of fast processors with built in 64bit floating point and mass memory claiming it can’t be done in 16K instead wanting 1M ie a matter of perspective… Cheers :-)
Forth on a PACE. Great stuff. A Kalman Filter in the 1970’s on a mini/micro? Pretty impressive. And you were doing the matrix multiply in fixed point or integer? Or could you unravel it into a series of more discrete calculations? (Or 1D Kalman?). Curious people want to know :-)
The modulo function can also be done with binairy AND, i.e.:
x%(2^8) is x&0x0FF
I’m using this trick frequently for circulair buffers (with the size of 2^n offcourse) to avoid reading writing outside it and wrapping around.
I’ve also used this for circular buffers, it’s so elegant I love it.
You might be interested in Zen of Assembly Language by Michael Abrash. There are all sorts of these “tricks” that become obvious once you learn more about computer architecture. The Zen of Code Optimization is another gem. If you are a programmer you owe it to yourself.
https://github.com/jagregory/abrash-zen-of-asm
Fixed-point math was a revelation to me when i discovered it. I was developing a sprite engine for the Nintendo DS and fixed-point math made a huge difference. Suddenly animations were much smoother and precise without any performance penalties
A topic always worth reviewing. Numerical analysis is I’m sure is a weak point for new hackers or something most of us never think about.
Rule of thumb: Don’t go against Knuth :-) But in the case that you are multiplying by a constant – for sure – really going to stay a constant – shifts and adds are great if you need the speed. Take the 72 x 12 example. 12 is 4 + 4 + 4 or 4 + 8 or 3 x 4. You have several choices if you are optimizing code. Shift the variable (72 in this case) left by 3 and add to the original shifted by 2. If you have registers or a stack available it is shift by 2 and push, shift by 1 and add. Or shift by 2 and add 3 copies together. It should take a microsecond or less on an 8MHz Arduino. (Guessing there. I wold have to look at the instruction set again to make sure). On an ARM it is 2 or 3 instructions.
Wozniak put the entire floating point routines for Apple II in 256 bytes of code, and they were long floating numbers in order to handle financials. Something isn’t right if a divide takes 500 bytes! Is that IEEE with all the boundary checking or something like that?
In my experience, the floating point routines in avr-gcc are surprisingly fast. I vaguely remember that the atmega328 has a hardware multiplier that speeds things up quite a bit. It comes down to some wasteful multiplies in really efficient hand-coded-by-a-compiler-pro functions. Also, for a sufficiently large and complex program, the code size of the flash routines is potentially amortized across the entire program and can result in an overall smaller program, as long as a function call site is less code than any inlined fixed point math. It’s definitely important to understand what your code is actually doing and balance your data type decisions on readability vs. necessary performance.
One trick you can do in floating point is turn division into multiplication. Any time you are dividing by a constant, you can instead multiply by (1.0/constant), and the compiler can then optimize away the division. Even if you don’t have a constant, you can always pre-compute the reciprocal if you are dividing multiple values with it. Remember kids, algebra is fun!
For a real example, I built an arduino mini based flight controller for my RC glider a couple years ago. It uses an integrated 3-axis gyro 3-axis accelerometer chip, the MPU6050. Although that chip can do onboard sensor fusion and output an attitude, I thought it would be fun to take the raw sensor readings and fuse the data together myself. I have that atmega328 doing floating point quaternion math estimating attitude at 100hz, and doing closed loop control of its RC servos at ~50hz. It is all written in fairly straightforward readable C++, and on top of that uses less than 20% of the available CPU cycles. I worried about floating point efficiency on that project until I measured it, and often times the floating point math was actually faster than the fixed point equivalent.
The tricky part about fixed point math is type promotion. When you multiply out a bunch of stuff you have to worry about overflow, so you end up having to cast values up to a larger type before multiplying. It’s very easy to end up with egregiously bloated code without realizing it. The frustrating thing is that CPUs with hardware multipliers often automatically promote types for you; you give the hardware 2 16-bit numbers and the result is a 32-bit output. Unfortunately, the C language syntax provides no way for you to describe that intent. If you multiply two 16-bit numbers you can only get a 16-bit result. If you cast the inputs to 32-bits you get a 32-bit result, but the compiler ends up also doing a full 32-bit multiply! At least with floating point, the software routines are written in highly efficient assembly and the hardware multiplier can be used to it’s full potential.
An eloquent counterpoint…
As a variation on this theme I often use the multiply and shift trick to re-cast native unit measurements into a sufficiently small real unit. I.e for the 10-bit ADC with a 3.13mV LSB, I’d convert that to milli-volts immediately. (3.13*16 = 50.08 so 50/16 or 25/8 is only 0.08/50 or -0.15% off)
Elliot, I love this series you have been doing, keep it up.
When converting float calculations to integer, if the value is always positive, remember to use unsigned ints, doubles the headroom for larger numbers. If you need to convert a 10 bit ADC value, multiply by 16 (4 bit shift) for example, then divide and divide by 16 again. 2^10 = 1024. 16 * 1023 = 16368. You can multiply by 64 too, 1023 * 64 = 65472, almost the maximum an unsigned 16 bit int can take.
Another thing to keep in mind, whenever you do a division, multiply by the maximum possible 2^x value before dividing to keep the accuracy.
Sometimes you can aggregate all the divisions and multiplications into one at the end. The fewer steps you take the better. If you multiply by x at some point, and divide by another number, you may be able to do that in one operation. ie
For a temperature sensor with 10mV per degree C (LM35):
temp = (ADCmax / Vref) * ADC * From_mV_To_Degrees_C.
temp = (1024 / 4.096) * ADC * 100
is equal to:
temp = (4.096 * 100 / 1024) * ADC.
temp = (0.4) * ADC
Or the same but multiplied by a factor of 10:
temp = 4 * ADC
temp = ADC << 4
This is convenient for a LED display, just display the temperature as an int, activate the decimal point on the display as needed. You don't need a float here.
When using a PIC16F1826 you can use the on board 4.096 voltage reference. If you only want 0..100 degrees C, you can drop the '<< 4' bit shift and take the ADC value directly by using the 1.024V reference. This is to illustrate that selecting the proper references, values, components etc you can make the code a lot simpler too.
Also remember that the fewer variables you use the faster it will be. If you store intermediary variables without using them anywhere else, merge them into one big expression. I've optimized the Marlin PID routine by eliminating the pid_Input = current_temperature variable and saved a few micro seconds and some ram in the process. I just use the current temperature variable.
The other trick for ADC converters…
Set up the voltage divider resistors, such that the ADC counts is the actual voltage in mV.
i.e. 10V = 1000 ADC counts.
Let the resistors do the division for you. ;)
LOL! Yeah, but floats are lousy because they’re lossy. Resistor division is lossy over more variables, so it just has to be lousier.
Fast, though.
For Arduinos running on 5V, try an ADC reference of 4.1V (4.096 to be precise).
For 3.3V systems, try a reference of 2.56V
You could explore a bit in the future of the series. For example you can do perfect error free math with rational arithmetic – if you have the RAM to handle numbers whose length can get out of hand if there is very much calculation involved. See Knuth again.
Precision is sometimes hard to understand. In a suggestion to move to floating point representation of time, I remember a very smart person suggesting that 55 seconds could be expressed in a 32 bit float – but also with nanosecond precision (a clock that counted nanoseconds).
One other trick I used at github.com/tz1/qrduino is to use counters instead of divides (modulo). For those who don’t know, QR Codes use a mask to avoid all white and all black areas, and some of them use “mod 3” in the calculation. Creating a counter that goes 0-1-2-0-1-2 uses one cycle, i.e for( x = 0; … t = x % 3; becomes for x = 0, x3 = 0 … x3++; if (x3 > 2) x3 = 0;
Another thing is if you are simply doing a compare or something else internal, you can multiply the other item, e.g.
x/3 > y v.s x > y*3 – but watch rounding v.s. truncation.
From the article: In particular, to divide any 8-bit number by thirteen, you first multiply the number by 158 (resulting in a 16-bit integer) and then drop the least-significant eleven bits. Yeah, right? It works because 158/211 ~= 1/13. It’s just math and it’s going to run about as fast as possible, but it’s not entirely readable.
Comment: This is where descriptive comments are valuable. I comment nearly every line of code and find it helpful in future readings.
Thanks for a good article, I agree. On micros I use integers as much as possible. Also, seems like a good technique to multiply by a constant and divide by a power of 2 when dividing by a constant.
OR first place, just don’t use lame micros (avr, pic, 8051, hc11 or whatever 8bit micro). Your time is more valuable than anything in the world. So use cortex M3, if you want to go small use cortex M0 which has a real barrel shifter.
Numbers don’t have feelings, you don’t need to try to defend their honor. Yikes.
People seem to want to have their feet on both sides; they want to accept unflinchingly that equality of floats can’t be expected, but then they want to have their foot on the other side and expect them to be “numbers” and the operations you do with them to be “math.”
However, when you try to add up those ideas, you can’t escape the result: floating point data points are not actually “numbers” in the mathematical sense, and that is why they can’t be compared. That is also why people doing important work with numbers don’t represent those numbers as floating point data; they represent them using numerical designations and functions that don’t just approximate math, but that are actually mathematically correct.
To the extent that an instance of floating point data is a “number,” it isn’t the number represented.
I don’t think anybody doubts that floating point data is very useful to graphical representation of data, and other special cases where you don’t need real math that follows the rules of… math, you just need an approximation of slightly better granularity than the screen pixels, or whatever. Just because you use them instead of numbers, and their colloquial name includes the word “number,” doesn’t mean they are actually the number being represented, or that the methods are doing “math” on the number purported.
Pedants, as usual for this site, really need to up their games. And pass pre-algebra.
They ARE numbers, a finite subset of the infinite set of all numbers, and therein lies the danger.
You missed my point. They might “be numbers” but they are not the numbers that they are representing, so it is a bit off-topic if they happen to be some _other_ different number. They’re numbers only in the sense that any digital data “is a number.” Which is to say, a pedant can argue it, but in the context of the usage, not all digital data is actually a number.
The representation can easily and explicitly have a precision that the floating point data instance simply doesn’t have. It isn’t actually the number represented. It just has everything named such that they sound like numbers. But they’re just a data representation that is number-like enough that it has many uses that would otherwise require actual correct math. So they have utility.
Perhaps your point would have been clearer if it didn’t contain counter-factual nonsense such as:
” expect them to be “numbers” and the operations you do with them to be “math.” ”
By your reasoning no operation on a CPU is “maths” because it is a finite state machine, well that is not true because symbolic computation is possible, then the limits become time and storage, not accuracy of computation because there is no ROUNDING ERROR.
Nice article once again.
I find that fixed-point number generally more accurately reflect the real-world that they are controlling. For instance, PID loop written using fixed point math will automatically saturate… floating point implementations have to be told not to go over 100% duty cycle but fixed-point algorithms do this naturally.
I’ll toss in my own plug now :) http://www.forembed.com/how-fixed-point-math-works.html
Awesome stuff! Thanks!
Another handy trick is to consider when looping is used in the math *and* your code is looping at the same time…
E.G. drawing pixels in a diagonal line with a slope of 3/5. You have to draw each pixel one-by-one in a loop anyhow, so rather’n doing the math (y=3/5 * x) for every pixel (in each iteration of the loop) along x, instead you can turn it into a sum using the previous value, something like y2 = y1+(3/5). And that, too can be simplified to integer-math (especially since there’re no fractional pixels) by noting that 3/5 is a division and division can be handled by looping (and you’re already doing a loop). Might require an extra variable or two, and some if-statements, but certainly faster for most uC’s than doing both a multiplication and a division (or floating-point) at every pixel.
Bresenham already sorted out the best way to draw sloped lines in pixels. All using integers. You essentially count in one axis in units of the other. Or something like that, been a while since I implemented it. He was an IBM bloke at the time, same as Mandelbrot was. Second only to Bell Labs, perhaps, as a genius-farm back in the day.
Man, I didn’t mean to get into floating point so much! Tackling it seriously is an entire article. Here’s a great one: http://docs.oracle.com/cd/E19957-01/806-3568/ncg_goldberg.html
My rules of thumb: Integers are exact, with the same resolution (one) over the whole range. If you need finer (constant) resolution, you go to fixed-point — which is really just re-defining your units to get rid of the fractions. The advantage of floats is an incredible dynamic range with a constant-percentage rounding error. When that’s what you need, you use floats.
Three different ideas, three different situations, three different solutions, all with their own traps and pitfalls.
The thing that I see (too much of?) is people using floats just because they have decimal places. It’s 1.2 kilometers to grandma’s house — we need a float! On second thought, it’s 1203 meters. Problem solved.
[Elliot Williams] Nice write up! It’s good to bring some awareness and better practices in coding.
I kept trying to dig up this one coding guide I read back in my late teens yesterday to no avail (wrongfully thinking it was regarding nethack).
Reading the comments I can say we have many really savvy folks (who have probably studied O notation and know the SICP by heart. I do not.)
This has served me well and since we are talking about a micro controllers (worrying about how well will a parallel AVR cluster will scale isn’t worth the headache.) this document here:
http://www.thangorodrim.net/development/caveman-programming-guide.html
should be clear enough to get folks to a quick answer without too much trouble.
28ms & 172 (or even 344)? Lot better then 32 ms and 500 bytes.
Funny how fast floats drive people to extreme anger one way or the other. One course in Principles of Computers (a 1001 course) and one in Computer Architecture (3001 I think, MIPS based) taught me what I needed to avoid them when I could and how to use them when I needed them: you try writing a raytracer without any floats at all; better to define an episilon and be done.
This is great. I got into fixed point for a recent embedded audio synth project. I spent a lot of time (inaccurately) converting back and forth from fixed to decimal notation while debugging, so I made a little calculator. It converts back and forth from fixed point (with whatever number of whole and fractional bytes).
http://adamarthurryan.github.io/q-calculator/
I especially had difficulty with a function where I needed to do lots of multiplication and division while managing the headroom. I had to change the radix several times and found it very confusing.
Informative post, thanks dude! :)
This reminds me of the articles at HP Museum, about calculator accuracy. The test they use is to evaluate (in degrees):
asin( acos( atan( tan( cos( sin( 9 ))))))
Most modern calculators use a microcontroller, and the accuracy of the final answer depends on the math library used (and memory limits when storing numbers to high number of decimal places).
See: http://www.rskey.org/~mwsebastian/miscprj/forensics.htm