If I asked you to find the area of a square, you would have no problem doing so. It would be the same if I asked you to find the volume of a cone or rectangle or any other regular shape. You might have to turn to Google to get the proper formula, but it would be a trivial process nonetheless. But what if I asked you to find the volume of some random vase sitting on a kitchen counter? How does one go about finding the volume of irregular shapes?
One way would be to fill the vase with much smaller objects of a known volume. Then you could add up the smaller volumes to get an estimate of the total volume of the vase. For instance, imagine we fill the vase with marbles. A marble is a sphere, and we can calculate the volume of each marble with the formula 
4/3πr3. We count all of our marbles and multiply the total by the volume of a single marble and arrive at our answer. It is not perfect, however. There is a lot of empty space that exists between the marbles as they fill the vase. We are forced to conclude that our estimated volume will be lower that the actual volume.
It would be about this time when our good friend Isaac Newton would ask the question “What if you made the marbles smaller?” Reducing the size of each marble would reduce the empty space that exists between them as they pile up in the vase, giving us a more accurate total volume. But how small? Is there a limit to how small we can make them? “Do not trouble yourself with the limit.” says [Newton]. “You will find that as you make the marbles smaller and smaller, you will begin to converge on a single number – and that number will be the exact volume of your vase.”
Reducing the size of the marble to get a more exact volume demonstrates the idea of the integral – one of the two fundamental principles of The Calculus. The other principle is known as the derivative, which we explained in our previous article by taking a very careful and tedious examination of an arrow in flight. In this article, we shall take the same approach toward the integral. By the end, you will have a fundamental understanding of what the integral is, and more importantly, how it works. Our vase example gives you a good mental image of what the integral is all about, but it is hardly a fundamental understanding of it. Just how do you make those marbles smaller? To answer this question, let us look again at one of Zeno’s moving arrows.
Drones or Arrows?
Imagine a drone on a collision course with a brick wall. Let us say that the drone moves from its starting point to a point half way between it and the wall. Let us repeat that process. If we keep moving between a starting point to a halfway point, how do we ever collide with the wall? Those who read our first article in this series would recognize this as a twist on the Dichotomy Paradox. Zeno, a philosopher from the 5th century BC, thought up the paradox and it took over two thousand years for mankind to answer it. In the last article, we solved his “the arrow” paradox with the derivative. In this article, we shall solve the Dichotomy paradox with the integral.
Those who have been paying attention will recall how the derivative and integral are actually inverses of each other or “two sides of the same ceramic capacitor” I think I put it. In the field of science and mathematics, practitioners like to find symmetry. There is a certain beauty…an elegance to a phenomenon when symmetry can be seen within its boundaries. With that in mind, recall how “the arrow” paradox asked what the velocity of a moving arrow is at an instant in time. In order to obtain the velocity, we needed to know its position at all times. The Dichotomy paradox is the opposite side of the same idea. Zeno is asking where the arrow drone is, or what its position is, at an instant in time. And in order for us to get a position on the drone, we need to know its velocity at all times. As luck would have it, our drone logs such data.
Case of the Wayward Drone
The Problem
Your automated drone project has an issue. It would appear you forgot a comma when programming its arduino brain, and it took off and got itself lost. Fortunately, the logging function appears to be intact. It was able to transmit its speed and heading for a period of 3 minutes. Unfortunately, its GPS was not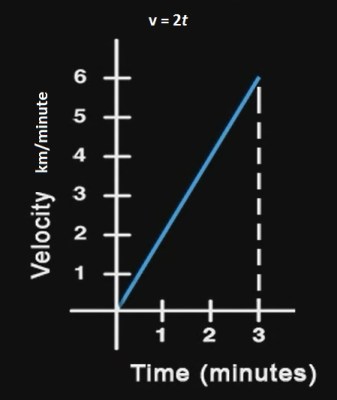 
working, so you do not have its location. Looking at the logs, you notice its heading never changed. It appears it flew North the entire flight. You also notice that the speed was not constant, but accelerating.
So here’s what you’ve got. You know the position of where it took off. You know that it flew in a straight line for a period of 3 minutes until the batteries ran out, and you can assume the drone went down at that point. You have the speed at all points in time within the three minutes, and work out that the drone was accelerating at rate of v = 2t. How do you find the location of the drone?
Now, if you’re thinking this sounds like a calc-101 word problem, you are correct! However, we’re not going to solve it by mindlessly plugging in data to an equation. We’re going to find our missing drone by solving the Dichotomy paradox. And by doing so, gain a perfect understanding of how the integral works.
The Solution
The speed of the drone was 2t or two times the time. Let’s say that after 1 minute of flight, it was moving at 1 kilometer per minute. After two minutes it was traveling at 4 kilometers per minute. And at the last line of the log detailing three minutes into its flight, our drone was traveling at a rate of 6 kilometers per minute. So how do we find out how far the damned thing went?
The best way to approach problems like this is to start off with the simplest example possible. Understand it, and then move up in complexity until we can get a handle on our real world problem. Keeping in this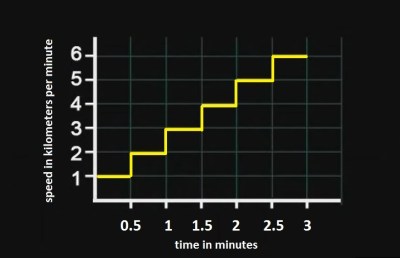 
light, let us pretend that the drone was traveling at a constant speed of 1 kilometer per minute. So after three minutes of flight, the drone would have traveled 3 kilometers. All we have to do is go to the launch pad and walk 3 kilometers in the North direction and we should find our drone.
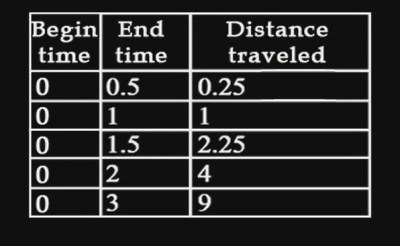
Now let us pretend that the drone was accelerating in increments. Such that at takeoff to the half minute mark, it was traveling at 1 kilometer per minute. From the half minute to the 1 minute mark, it was traveling at 2 kilometers per minute. Every 30 seconds, the drone increases its speed by 1 mile per minute until its 3 minutes of flight time are up. Let us look at the graph on the right and calculate the distance traveled. If distance is equal to time multiplied by speed, then:
Total distance traveled is:
Finding how far the drown traveled is pretty simple when speeds are constant. Unfortunately the real world doesn’t usually work like this. Our drone was accelerating at a constantly changing rate of 2t for 3 minutes. How do we deal with this? Well, we know how to add up the pieces at constant speeds to get a total distance traveled. What if we could take the speed of our accelerating drone and break it into little pieces, calculate the average distance traveled during the little pieces, and then add those pieces of distance traveled up to get a total? Much in the same way we broke the area of our vase into little spheres and added them all up.
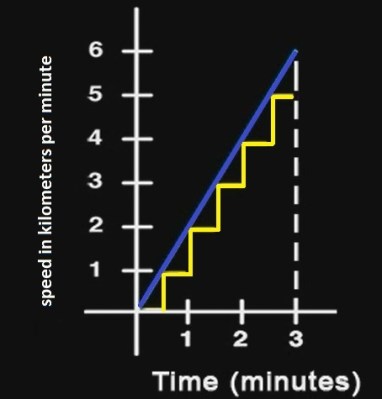
The easiest way to do this is to create what I call a ghost drone. What the ghost drone will do is tail our real drone that is moving at speed 2t (blue line in the graph on the left). But the ghost drone will move with an incremental speed like in our hypothetical example above (yellow line in the graph on the left). We’ll calculate the total distance traveled of our ghost drone to get an estimate of the distance traveled of our real drone.
Here’s what I mean by tail. Let us imagine that when our real drone took off, the ghost drone stayed on the ground. But as soon as the real drone hits the 0.5 minute mark, the ghost drone instantly obtains a speed equal to that of the real drone. It then maintains this constant speed as the real drone continues to accelerate. As soon as the real drone hits the one minute mark, the ghost drone once again instantly increases its speed to match the real drone. And once again, it maintains that speed as the real drone continues to accelerate at a rate of 2t. Look at the graph on the left and see that the ghost drone continues the process of tailing the real drone up until the end.
Why are we doing this? Because we know how to calculate the total distance traveled of the ghost drone.
Total distance traveled of ghost drone is:
Because our ghost drone is always lagging the the real drone, this estimate will be an underestimate of the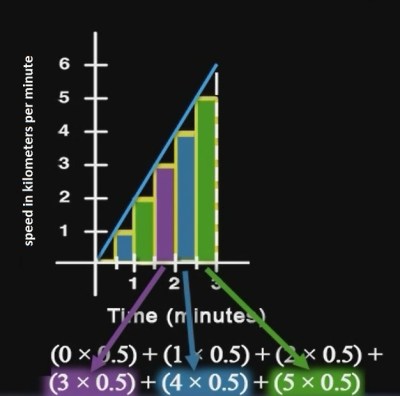
distance traveled of the real drone. Ideally, we’d perform the same procedure with another ghost drone that was persistently outrunning the real drone, giving us an overestimate of the real drone’s total distance traveled. But to keep things as simple as possible we’ll just use our underestimate.
So we have an estimated distance traveled of 7.5 kilometers North of the launch point. At this point we need to see what we can do to make that estimate more accurate. Those who have been following this calculus series will know that we can get a more accurate estimate of the distance traveled by the real drone by taking finer and finer time intervals when calculating the distance traveled from our ghost drone. Looking at the graph on the right, you can see that the width of the vertical rectangles are actually the time intervals of our measurements. If we make this width smaller, we can fit more of them under the v = 2t function (blue line) and reduce the space not occupied by the rectangles. It’s the same concept as making the marbles in our vase smaller to reduce the empty space between them.
Instead of using half minute intervals, let’s see what happens when we take 1/10th minute intervals.
Total distance traveled of ghost drone is:
This is becoming a very laborious process, but a necessary one. As you keep calculating the estimated distance traveled with finer and finer time intervals, you will begin to converge on a single number: 9. The same number would appear if we did overestimate calculations. We can now say that our drone traveled a distance of 9 kilometers. And we can also say that we can know the distance the arrow traveled in the Dichotomy paradox, regardless of its velocity.
The Power of the Integral
So you go to your launch point and head 9 kilometers North and locate your drone. You get it home and realize the camera was running during the entire flight. You take a look at the video and become curious at some of the landmarks. You begin to wonder where they are. You just worked out the total distance traveled by the drone…is it possible to find the distance between the launch site and some of the landmarks of the video? Of course! As long as you have the time when the drone flew over the landmark, you can bounce it off the logs to get the speed. Let us imagine doing the exact same labor intensive process as we did above, but for different lengths of time. Instead of getting the distance traveled in three minutes, let’s try half a minute, two minutes and so forth….times that correspond to our drone flying over the landmarks. How far did our drone travel to reach them?
The pattern is obvious. For the given function f(x) = 2x, the integral is x2. If you recall from our last article in this series, the derivative of the function f(x) = x2 is 2x. Now we see how they are inverses of each other. It will be the relationship between these two fundamental principles of calculus, the derivative and the integral, that will be the subject of the next article.
Sources
All images are from The Teaching Company course, Lecture 3.
tl;dr.
show me some cool avr hack or new IoT devices, not some boring math lectures.
I really hope this is satire. If the goal was to mock the ignorance of youth it was spot-on.
Would you please not insult an entire group, just because some members are clueless, honestly I doubt you’re generation was any better. Honestly about the same percentage of adults and children know nothing about electronics or math so stop just picking on kids because there an eaiser target. Yeah the guy above was a troll, but your not any better.
The “ignorance of youth” isn’t a demographic. It’s an attribute of inexperience. Since I didn’t specify an age threshold as being “young”, getting upset with me for being bigoted is nonsensical.
Would you be offended if I lamented the blissfully ignorant as well?
I think the expression is “if the shoe doesn’t fit”, however I AM flattered you assumed I’m not Generation Y myself…
#dealwithit #trollisnotaninsult #woosh
Oh, f*ck off.
“*Boo-hoo* people have different tastes, opinions, and levels of knowledge than I do and this site is not catering to me exactly, at all times, with every article, *Wah wah wah.*”
You knew it was a math lecture when you saw the title. If you find math lectures boring, don’t click on the bloody link. This isn’t rocket science.
>integrals
>not rocket science
you might want to think about that statement a little more….
>flour
>not cake
‘Nuff said?
in a few years time you’ll be hateful of anything IoT when you can’t even shit without an IoT Toilet connecting to your facebook to post updates on your ass’ behalf
Seriously an article about high school math? Not a particularly great explanation of the topic either, especially considering how long winded it is. Yet another step toward this site becoming lame-a-day
Not everyone knows this stuff. I found it fascinating because I never took calc (nearly failed high school math, actually). I really enjoyed the way the articles walk you through the mechanics of it.
Well, some of it is even outright wrong. For example:
“Reducing the size of each marble would reduce the empty space that exists between them as they pile up in the vase”
No it wouldn’t, because the volume taken up by the balls shrinks at the same rate as the empty volume between the balls, the ratio between the two remaining the same. If you don’t know this stuff already, you should read introductory material done by competent teachers instead of this.
Yep. Assuming the marbles are all the same size (implied by the “count all of our marbles and multiply the total by the volume of a single marble” statement), you’ll converge on about 75% of the total volume (making some other assumptions, like the packing is dense). You do better if the marbles are different sizes.
And I love calculus, but if I really needed to know the volume of a vase of irregular shape- I’d fill it with water then pour the water out into a graduated cylinder or other container of known volume.
What the world needs is better word problems.
Oh, the whole approach is wrong of course. There is a particularly fitting anecdote according to which a mathematician, a physicist and an engineer are all given the same little red ball and asked to find its volume. The mathematician of course measures the diameter and calculates the volume. The physicist dunks the ball in a cup full of water and measures how much spilled out. The engineer – he walks up to his cabinet, picks up the little red ball catalogue, and looks up the nominal volume… ;)
I disagree with this being lame, maybe you know it, but I am sure plenty of the readers do not – I know it, but still like refreshers… if only for the narrative.
One thing that dis appall me, is the ‘catchy title’, I was brought into this post expecting completely different content. If this was title appropriately I still would’ve clicked it, because such articles are rare on hackaday.
Didn’t read it fully yet, interesting topic! For the time being: would you please fix the volume of the sphere in the beginning? Cheers!
(at the beginning, sorry)
Another problem that is not mentioned is that spheres will always have an excluded space even with optimal packing. As the size of the sphere approaches zero, the sum of the volume of the spheres will need to be multiplied by 3*sqrt(2)/pi to equal the total volume. See https://en.wikipedia.org/wiki/Sphere_packing
No matter how small the spheres are, there is always pi/(3*sqrt(2)) or ~74% that is empty space.
If you use infinitely small grains of sand (cubes), no such problem. Also, easier to integrate vase volume using stacked discs with height approaching zero. Captain pedantic signing off.
Another thing, are those really Newton quotes? Sounds almost Yoda-esque. “Trouble yourself not with the limit.” “Converge upon a single number, you will (with correction you must).”
The original text was probably written in Latin, the weirdness is likely from the translation.
The example is less than ideal. I would give an A to any student who just said “fill it with water”.
Would water molecules be small enough for you?
I’d seal the top, then dip the vase in water. Measure the volume of water displaced.
The volume of displaced water is equal to the volume of the vase.
Sure- but that works because the way you measure water takes into account the ‘packing fraction’. If you tried to measure the volume taken up by a single water molecule and multiply by the number of molecules, like this post does, you’d get the wrong answer then, too.
You are still using water to measure it. Let’s say you use gravel, It can hold 2 liters of gravel, or displace 2 liters of gravel. Now if you displace 2l of gravel but it holds 2.4 l of water you have increased your precision not by measuring a different side but using a medium with a better packing ratio.
That’d give the volume of the OUTSIDE, not the volume of the inside.
Yes, this gives the volume of the OUTSIDE of the vase. That’s the correct answer for “volume of a vase”.
Although, technically, you should follow up with putting water inside, measuring that – and subtract.
The difference is the volume of the vase itself, rather than the volume it contains.
Ouch, yes, very true, indeed! :-o Thanks for pointing that out. Really embarrassing. And has nothing to do with pedanticism, it’s actually quite gross! :)
(I meant to react to this, BTW: “No matter how small the spheres are, there is always …% … empty space.”)
There is a little mistake for the volume of a sphere, you wrote 4/3πr² instead of 4/3πr³.
Fixed. THanks!
Good article. I never took Calc in school but have stumbled my way though it in life since. It would seem as though this doesn’t account for the ballistic motion of the drone once the battery dies. Rather, this assumes the immediately falls straight down. May not be an issue on the big picture, but seems important nonetheless.
I’ll elaborate a little further:
For the given function f(x) = x^2, the indefinite integral is [(x^3)/3] + C.
For the given function f(x) = x^3, the indefinite integral is [(x^4)/4] + C.
etc…
Indefinite integrals are used for finding the general form of the integral, while the definite integral is used to find the area within a specific interval of the indefinite integral. Supposing you want to know the distance traveled in 60 seconds: the initial position “+C” is irrelevant to the distance traveled.
How is this calculated?
https://en.wikipedia.org/wiki/Fundamental_theorem_of_calculus#Second_part
More simply stated:
You take the position at the finish time(“60 seconds”) and subtract the position at the start time: “0 seconds”
Position(in meters) as a function of time(in seconds):P(t) = (t^3)/3 + C
Velocity as a function of time(in seconds):V(t) = (t^2) [Note: the derivative of “+ C” is: “+ 0”]
Acceleration as a function of time(in seconds): A(t) = 2(t)
So returning to the original problem: [(60^3)/3 + C] – [(0^3)/3 + C] = (60^3)/3 + C – C which is the same as (60^3)/3 meters traveled.
For those of you who haven’t already and don’t wish to attend 2-3 semesters of college calculus: much of what is taught in college calculus classes are how to find more complex integrals/derivatives than simple polynomials(which require no more than the “power rule”) and to do so by hand. For the impatient and more interested in the application of these skills to things like writing code and making spreadsheets: Wolfram Alpha and SymboLab both have indefinite integral solving features for arbitrary functional inputs.
http://www.wolframalpha.com/calculators/integral-calculator/
https://www.symbolab.com/solver/indefinite-integral-calculator
Now: you will not always be provided a functional description of behavior. In some cases: Physics classes will help you identify these functional descriptions for a few measurements/sensor values. In other cases: you will not know the underlying governing equations dictating whatever is being measured. In these cases, there are several strategies available.
1) Riemann Sums/Trapezoidal Rule/Simpson’s Rule:
http://www.cplusplus.com/forum/general/30434/
http://www.cplusplus.com/forum/general/79581/
http://blog-noxasch.blogspot.com/2014/11/c-using-simpsons-rule-to-numerically.html
These methods of finding a definite integral do not require a functional description and can be solved entirely through numeric analysis.
2) Use a polynomial regression solver
http://www.arachnoid.com/polysolve/
This is more of an “offline” methodology, however if you have several data points, you can “fit” an n-degree polynomial curve to those datapoints and then use symbolab/wolfram alpha to find the indefinite integral of that curve. Converting the indefinite integral to a c++/Python/Java function should at that point be fairly straight-forward.
A little knowledge is a dangerous thing, and there is the danger of “overfitting” a polynomial and finding patterns that don’t exist in noisy sensor measurements. Sometimes you can use a strategy called “dimensionality reduction” to reduce the inputs to the most significant thereby eliminating sources of noise which do not play a significant role in governing the behavior.
3) Use a neural network to do regression
http://www.dspguide.com/ch26/1.htm
http://cs.stanford.edu/people/karpathy/convnetjs/demo/regression.html
This is a little exotic, but in many cases: neural networks can be very powerful tools for creating predictors based on training data/datapoints.
Closing thoughts:
Finding position provided with only accelerometer input is a classic problem known as inertial navigation. The difficulty lies in the fact that any error in the acceleration measurement will increase exponentially in the process of integration to find velocity, and any error in the velocity will increase exponentially in the process of finding position.
These are the things I wish that I understood about calculus when I started college.
Nice add-on to the topic! I also wish that I knew this spectrum of tools in my first years of college. This definitely may encourage new students to understand real applications of calculus.
Neural network for solving integrals!?!? You kids and your rocket cars get off my lawn!
Seriously: any approach to estimating an integral numerically either ends up in picking an approximating function, for which the integral is easily calculated, or in picking a bunch of points along the curve, evaluating the function at those points and summing up rectangles/trapezoids.
With neural nets, as with splines or polynomial approximations, you’re using an approximating function. How well the neural network (a sum of weighted sigmoids) works is problem-dependent. Sometimes it’ll work well and other times it will over-fit as with splines. “Just use a neural network” presumes an ass-ton of user expertise: it’s like trying to drive to the supermarket as quickly as possible and “just using an Indy car”. You might be better off thinking about a shorter route.
Similarly Monte Carlo integration is just letting a random number generator pick your evaluation points, rather than using a disciplined formula like with Simpson’s rule. This can work better, but there’s no reason to expect that it _must_.
In short, Simpson’s rule almost always suffices. If you know more about your particular function, then by all means use that information.
Will, please ignore the people posting negative comments about the article being dull or lowbrow. There are plenty of us that are lapping them up.
More please????
More please.
I enjoy the different take on a relativity boring topic
More indeed; relativity boring sounds fascinating. What is it? Mining black holes for anti matter?
I guess the volume of the marble in second paragraph is 4/3πr^3 and not 4/3πr^2.
yes, volume, so 3rd power, caught my attention too.
“”“What if you made the marbles smaller?” Reducing the size of each marble would reduce the empty space that exists between them as they pile up in the vase, giving us a more accurate total volume””
Does it though, each sphere occupies 4/3*pi*r^3. If the spheres are packed together there is some ratio of their inner volume to the volume of space they ‘control’ so to speak ( where other spheres control volume cannot share this space).
If this is true the limit of the spheres sum volume does not converge to the vase volume as they are made smaller.
Does anyone know why the ratio should not be a constant as the size diminishes of each sphere.
As they become infinitely small, so will the empty space, 0*anything is… zero
Yes, but the proportion of empty space to filled space will remain the same, the only thing that improves are the edges to the vase. So the solution does not tend toward the volume of the item. It tends to toward the volume multiplied by the fill factor, in this case of randomly packed spheres.
If you think about looking at tiny spheres through a microscope, they look exactly the same as big spheres, and appear to occupy the same proportion of space. If someone gave you a picture containing only spheres at an unknown magnification and asked you to work out the size of the spheres you couldn’t do it.
This said if you measure the volume of tiny-marble-sand by filling another container of easy to work out volume, like a cylinder, then the fill factor cancels out.
But as a mathematical explanation “Reducing the size of each marble would reduce the empty space that exists between them as they pile up in the vase, giving us a more accurate total volume. ” isn’t true, because the volume of the spheres reduces in proportion to the volume of the space (except the edges).
@Marvin: you’re spot on here. It would have been cleaner if Will used cubes. Maybe.
The general point is that the spheres fill in the edges better and better, making the volume of the spheres a better and better approximation of (a fixed fraction of) the true volume. This intuition is the same as for the cubes, but it’s off by a factor of 3*sqrt(2) / pi.
As you say — the factor cancels out. When you pour sand into a vase, and then pour it out and into a (say) cube of known volume, you can nonetheless figure out the volume of the vase. The same thing goes for the spheres, and smaller spheres will fill up a larger cube when you pour them out. So in that sense, Will’s spheres are totally ok.
The part that bugs me: if you do the same with sand, or water — real physical sand or water — you’ve got probably the same amount of wasted volume or more. Taking a microscope to sand grains, they’re not cubes, and some of them have crazy space-wasting shapes. Certainly at the atomic level, electron-around-nucleus scale, everything’s space and nothing’s actually matter. So maybe the pour-out-into-another-container method _is_ the ground truth rather than the mathematical approximation. (Coastline paradox and all that.)
“Improves at the edges” is all the integrating cubes do as they get smaller, too. Isn’t that where all the action is?
TL;DR: cubes makes the abstract math work out right (dx dy dz and all that), but the Greeks had marbles and they got the intuition right.
Which greek measured the volume of an irregular object (the kings crown, suspected to contain lead) using water? Aristotle? Archimedes?
I’ll give you a clue – Eureka!
No, won’t converge with spheres. Look at it this way. If you leave the marble size alone and make the vase bigger by a factor of 100, does it change the proportion of empty space around the marbles? 10,000 times bigger? Obviously no.
You need a little differential of volume. A dxdydz is a cube. A dzdr*da (angle) is a pie piece, etc. They have to fill the space.
Spot on. The article needs to be edited to fix this misleading error; as others point out, you can use it as a more accurate approximation, but you have to measure the volume taken up by the marbles in a regular container, or you have to account for the packing fraction of the marbles – not just use the actual volume of a spherical marble.
Streetfighting mathematics, it’s approximately a cuboid. Job done.
https://mitpress.mit.edu/sites/default/files/titles/free_download/9780262514293_Street_Fighting_Mathematics.pdf
Keep it up with the maths :) I started learning mathematical modelling recently and it has rekindled my interest in it. It’s nice to see how the things you learn by rote at school are actually useful for solving or getting a better grasp on a huge range of real problems.
If you don’t know this by the time you graduate high school, your country needs to FIRE your high school teachers!
I’m liking this series, keep ’em coming please! I haven’t yet read the derivative article but I will do.
I stuck badly at maths, but ever since I learned about the ubiquitous engineering magic that is the PID algorithm, I’ve wanted to *properly* understand it without dragging myself through stale maths books.
Please tell me the series will be heading towards PID algorithms cos that would be awesome.
Oh, and is pretty ironic that you’re using the drone travel distance example, when drones traditionally use the PID algorithm to maintain their spatial orientation!
I can see why though, given it’s not a way to approach learning it from a beginners perspective.
Interesting. I assumed drones used a combination of PID and Kalman filtering (which you will never understand – good thing somebody wrote a lib).
I’ve taken calculus 3, differential equations, and numerous engineering classes but for the vase problem I’d weight it empty and again full of water (distilled preferred) instead of using any calculus.
“The vase” is the interior volume of an oil tanker. Or “the vase” is microscopic.
Math is still useful even if you’ve got good scales and you know your local gravity pretty well. (Pedants would suggest using a balance.)
You missed my point, maybe going the other direction will clarify. You wouldn’t even need a scale or balance if you knew the flow rate of water filling the vase and the total time of flow. Oh wait no flow meter, so I’ll set up a tank and put in a simple hole of known diameter so that I can use more math to figure out the solution to what is the volume of a vase. Each step you add into the process can introduce errors.
It really comes down to having the function that describes the space. If it takes more time to formulate the equation than to find the volume with practical measurements you are wasting time/money.
Also, the oil tanker should be clearly marked with capacity, with CAD models or at least blueprints available from the manufacturer.
I sincerely love all the people complaining about math, but then go on to post their little microcontroller projects without irony.
Math is the basis for nearly every digital system we have. Its not ‘boring’ it describes real events and systems. This goes a long way towards discussing analyzing systems and their variables.
Ha I have the seventh edition of that textboook sitting on my desk from my Calc course last term.