People tend to obsess over making computer software faster. You can, of course, just crank up the clock speed and add more processors, but often the most powerful way to make something faster is to find a better way to do it. Sometimes those methods are very different from how a human being would do the same task, but it suits the computer’s capabilities. [Nemean] has a video explaining a better multiplication algorithm known as Karatsuba’s algorithm and it is actually quite clever. You can see the video below.
To help you understand the algorithm, the video shows a simple two-digit by two-digit multiplication. You can see that the first and last digits are essentially the result of one multiplication. It is all the intermediate digits that add together. The only thing that might change the first digit is a carry.
Using clever math, you can compute the first and last digit, along with a sum that contains the middle parts added to the first and last digits. By subtracting them out, you can get all the required digits using fewer multiplications than the traditional method. Adding and subtracting is generally cheap, so trading those for multiplications can result in major time savings.
Of course, these days your multiplication probably occurs in hardware but it still may not be as fast as addition and subtraction. The complexity of this algorithm, though, means it isn’t often used unless you are dealing with very large numbers. Either way, it is a clever application of math and disproved what “everyone” knew — that the best method had already been found. It makes you wonder how many other known things will be disproven in the future.
We are always interested in odd math methods. Some of them are rather colorful.

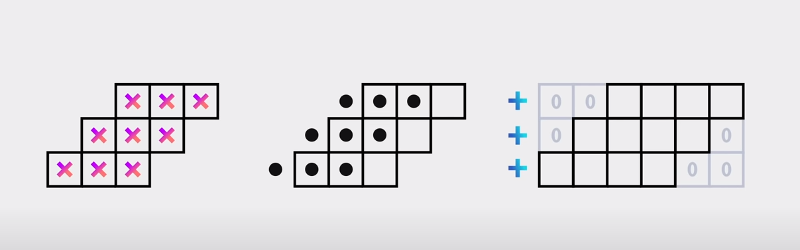














I like the algorithm and started reading around the subject, and on Wikipedia I found this “As a rule of thumb, Karatsuba’s method is usually faster when the multiplicands are longer than 320–640 bits”. And I though about how multiplication in base 2 is mostly bit shifts and addition, and went that probably makes sense. But then I started to wonder what multiplication calculations are done that require accuracy to 320+ bits ?
Public key cryptography techniques like RSA and Diffie-Hellman require modular exponentiation using thousands of bits. That tends to require lots of multiplications of huge numbers.
“Adding and subtracting is generally cheap, so trading those for multiplications can result in major time savings.”
Interestingly, in binary multiplication multiplying two bits requires a single and gate, and is much faster than the additions. This leads to innovations such as Wallace trees and Dadda trees to speed up the additions.
That’s why Karatsuba’s algorithm doesn’t win for the small sized numbers found in most CPUs.
https://en.wikipedia.org/wiki/Wallace_tree
https://en.wikipedia.org/wiki/Dadda_tree
The Schönhage–Strassen algorithm is faster than Karatsuba for numbers with more than several tens of thousands of digits. I guess it doesn’t get much use in everyday arithmetic.
That and even faster algorithms are mentioned in the video, including David Harvey and Joris van der Hoeven’s O(n log n) algorithm which is only faster for numbers having more than 2^(1729^12) bits. That’s the number of bits in the numbers, not the values of the numbers.
Handy for calculating tips ;)
This video was included in the “Summer of Math Exposition #1”, organized by James Schloss and Grant Sanderson:
https://www.3blue1brown.com/blog/some1-results
If you’re looking for more of this sort of thing, the full playlist of video entries is here:
https://www.youtube.com/playlist?list=PLnQX-jgAF5pTkwtUuVpqS5tuWmJ-6ZM-Z
And then there’s every engineers favourite hammer, the lookup table.
Mathematicians only have screwdrivers.