Count Leading Zeros For Efficient Logarithms

February 7, 2023 by Chris Lott 14 Comments

[Ihsan Kehribar] points out a clever trick you can use to quickly and efficiently compute the logarithm of a 32-bit integer. The technique relies on the CLZ instruction which counts the number of leading zeros in a machine word and is available in many modern processors. Typical algorithms used to compute logarithms are not quick and have a variable execution time depending on the input value. The technique [Ihsan] is using is both fast and has a constant run time.

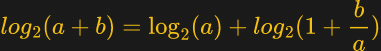
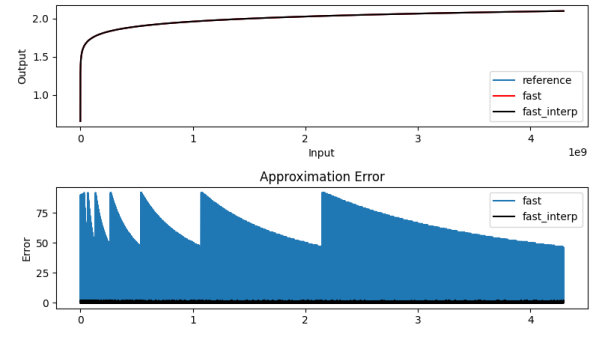
The above equation summarized the math behind the algorithm. We get the first term easily using the CLZ instruction. Using the remainder and a pre-computed lookup table, it is possible to get the second term to various degrees of accuracy, depending on how big you make the table and whether or not you take the performance hit of interpolation or not — those of a certain age will no likely groan at the memory of doing interpolation by hand from logarithm tables in high school math class. [Ihsan] has posted an MIT-licensed implementation of this technique in his GitHub repository, which includes both the C-language algorithm and Python tools to generate the lookup table and evaluate the errors.

Why would you do this? Our first thought was real-time streaming DSP operations, where you want fast and deterministic calculations, and [Ihsan]’s specifically calls out embedded audio processing as one class of such applications. And he should know, after all, since he developed a MIDI capable polyphonic FM synthesizer on a Cortex M0 that we covered way back in 2015.

Dithering Makes Everything Cooler: Now Even Animated

July 4, 2022 by Elliot Williams 37 Comments

[dukope] was writing a game, Return of the Obra Dinn, with a fantastic visual style. One of the choices was to make everything in glorious one-bit color, otherwise known as black and white, and then dither it back to monochrome. You know, like they used to do on the Mac Plus.

If dithering is your aesthetic, then it makes a ton of sense to take it seriously. And it’s absolutely beautiful – check out the video below.

But what’s even more amazing is [dukope]’s attention to detail on the dithering. For instance, this post on the TIG forums details the problems and solutions when you have a dithered image that needs to also be animated. You want the dots to stay relatively constant on the object as the virtual camera pans across the scene, and that’s going to necessitate a custom algorithm. And if you think that’s cool, have a look at how the book at the center of the game is animated.

What can we say. We loved dithering before, but this post has made our love even deeper.

Continue reading “Dithering Makes Everything Cooler: Now Even Animated” →

Linux Fu: Roll With The Checksums

June 22, 2022 by Al Williams 14 Comments

We are often struck by how often we spend time trying to optimize something when we would be better off just picking a better algorithm. There is the old story about the mathematician Gauss who, when in school, was given busy work to add the integers from 1 to 100. While the other students laboriously added each number, Gauss realized that 100+1 is 101 and 99 + 2 is also 101. Guess what 98 + 3 is? Of course, 101. So you can easily find that there are 50 pairs that add up to 101 and know the answer is 5,050. No matter how fast you can add, you aren’t likely to beat someone who knows that algorithm. So here’s a question: You have a large body of text and you want to search for it. What’s the best way?

Continue reading “Linux Fu: Roll With The Checksums” →

Our Favorite Things: Binary Search

March 16, 2022 by Elliot Williams 34 Comments

You might not think that it would be possible to have a favorite optimization algorithm, but I do. And if you’re well-versed in the mathematical art of hill climbing, you might be surprised that my choice doesn’t even involve taking any derivatives. That’s not to say that I don’t love Newton’s method, because I do, but it’s just not as widely applicable as the good old binary search. And this is definitely a tool you should have in your toolbox, too.

Those of you out there who slept through calculus class probably already have drooping eyelids, so I’ll give you a real-world binary search example. Suppose you’re cropping an image for publication on Hackaday. To find the best width for the particular image, you start off with a crop that’s too thin and one that’s too wide. Start with an initial guess that’s halfway between the edges. If this first guess is too wide, you split the difference again between the current guess and the thinnest width. Updated to this new guess, you split the differences again.

But let’s make this even more concrete: an image that’s 1200 pixels wide. It can’t get wider than 1200 or thinner than 0. So our first guess is 600. That’s too thin, so we guess 900 — halfway between 600 and the upper limit of 1200. That ends up too wide, so we next guess 750, halfway between 600 and 900. A couple more iterations get us to 675, then 638, and then finally 619. In this case, we got down to the pixel level pretty darn fast, and we’re done. In general, you can stop when you’re happy, or have reached any precision goal.

[Ed note: I messed up the math when writing this, which is silly. But also brought out the point that I usually round the 50% mark when doing the math in my head, and as long as you’re close, it’s good enough.]

What’s fantastic about binary search is how little it demands of you. Unlike fancier optimization methods, you don’t need any derivatives. Heck, you don’t even really need to evaluate the function any more precisely than “too little, too much”, and that’s really helpful for the kind of Goldilocks-y photograph cropping example above, but it’s also extremely useful in the digital world as well. Comparators make exactly these kinds of decisions in the analog voltage world, and you’ve probably noticed the word “binary” in binary search. But binary search isn’t just useful inside silicon. Continue reading “Our Favorite Things: Binary Search” →

Hacking Multiplication With Karatsuba’s Algorithm

November 16, 2021 by Al Williams 8 Comments

People tend to obsess over making computer software faster. You can, of course, just crank up the clock speed and add more processors, but often the most powerful way to make something faster is to find a better way to do it. Sometimes those methods are very different from how a human being would do the same task, but it suits the computer’s capabilities. [Nemean] has a video explaining a better multiplication algorithm known as Karatsuba’s algorithm and it is actually quite clever. You can see the video below.

To help you understand the algorithm, the video shows a simple two-digit by two-digit multiplication. You can see that the first and last digits are essentially the result of one multiplication. It is all the intermediate digits that add together. The only thing that might change the first digit is a carry.

Continue reading “Hacking Multiplication With Karatsuba’s Algorithm” →

Taking A Crack At The Traveling Salesman Problem

October 21, 2020 by Matthew Carlson 16 Comments

The human mind is a path-planning wizard. Think back to pre-lockdown days when we all ran multiple errands back to back across town. There was always a mental dance in the back of your head to make sense of how you planned the day. It might go something like “first to the bank, then to drop off the dry-cleaning. Since the post office is on the way to the grocery store, I’ll pop by and send that box that’s been sitting in the trunk for a week.”

This sort of mental gymnastics doesn’t come naturally to machines — it’s actually a famous problem in computer science known as the traveling salesman problem. While it is classified in the industry as an NP-hard problem in combinatorial optimization, a more succinct and understandable definition would be: given a list of destinations, what’s the best round-trip route that visits every location?

This summer brought news that the 44-year old record for solving the problem has been broken. Let’s take a look at why this is a hard problem, and how the research team from the University of Washington took a different approach to achieve the speed up.

Continue reading “Taking A Crack At The Traveling Salesman Problem” →

An Algorithm For De-Biasing AI Systems

October 21, 2019 by Sharon Lin 52 Comments

A fundamental truth about AI systems is that training the system with biased data creates biased results. This can be especially dangerous when the systems are being used to predict crime or select sentences for criminals, since they can hinge on unrelated traits such as race or gender to make determinations.

A group of researchers from the Massachusetts Institute of Technology (MIT) CSAIL is working on a solution to “de-bias” data by resampling it to be more balanced. The paper published by PhD students [Alexander Amini] and [Ava Soleimany] describes an algorithm that can learn a specific task – such as facial recognition – as well as the structure of the training data, which allows it to identify and minimize any hidden biases.

Testing showed that the algorithm minimized “categorical bias” by over 60% compared against other widely cited facial detection models, all while maintaining the same precision of detection. This figure was maintained when the team evaluated a facial-image dataset from the Algorithmic Justice League, a spin-off group from the MIT Media Lab.

The team says that their algorithm would be particularly relevant for large datasets that can’t easily be vetted by a human, and can potentially rectify algorithms used in security, law enforcement, and other domains beyond facial detection.