The Calculus is made up of a few basic principles that anyone can understand. If looked at in the right way, it’s easy to apply these principles to the world around you and to see how the real world works in their terms. Of the two main ideas of The Calculus — the derivative and the integral — today we’ll focus on the derivative.
You can enjoy this article by itself, but it is also worth looking back at the previous installment in this series. We went over the history of The Calculus and saw how it arose from two paradoxes put forth by a 4th century philosopher named Zeno of Elea. These paradoxes lead to the derivative/integral ideas that revolutionized mankind’s understanding of motion.
The derivative is what is necessary to solve Zeno’s “The Arrow” paradox. In this paradox, Zeno asks how an arrow flying through the air can have a velocity at an instant in time. For at each instant, the arrow is still. Before we begin with our process of discovering the answer — a process that took civilization over two thousand years to figure out — let us refresh our static memory with our previous description of the derivative:
The Derivative – The derivative is a technique that will allow us to calculate the velocity of the arrow in “The Arrow” paradox. We will do this by looking at positions of the arrow through incrementally smaller amounts of time, such that the precise velocity will be known when the time between measurements is infinitely small.
Is It Really This Simple?
I think you will find that it is, and even wonder why it took civilization so long to figure it out. Zeno wants the velocity of the arrow. In order to calculate velocity we need two things – time and position. Velocity is just distance divided by time, such as miles per hour or feet per second. If we measure the distance traveled by the arrow and divide it by the time it took to move the distance, that is by definition the velocity of the arrow.
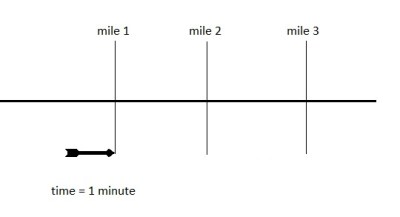Let us assume that the arrow is moving at a constant velocity (this will be important later). Then let us place markers every mile along the path of the arrow. With the addition of a watch on our wrist, we have everything in place to measure the arrow’s velocity. We watch the arrow fly through the air and mark the position of the arrow when our watch reads 1 minute. Let us suppose this position corresponds to the 1 mile marker. We then mark the position of the arrow when our watch reads 2 minutes, which happens to be at the 2 mile marker. Using basic math, we can find the average velocity of our arrow. To keep things simple, we’ll use the measurement unit of miles per minute for velocity, allowing us to say that our arrow was traveling with an average velocity of 1 mile per minute.
The important thing to understand is that we take a final position, which is p(2), subtract the initial position, p(1), and divide the difference by the time it took to cover the distance. This is the fundamental understanding of motion from a mathematical point of view. That the arrow is at one point at one time, and another point at another time.
N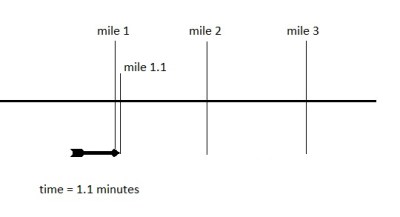
ow that we have an average velocity between two points in time, we can begin to refine our process. Zeno wants to know the velocity at an instant in time. Not between two points in time. Well, we know the average velocity between the 1 minute and two minute time points. What’s to stop us from shrinking the difference? Let us find the velocity of the arrow between the 1 minute and 1.1 minute time points. These two points in time are much closer together, and would give us a better idea of what the velocity was at exactly 1 minute.
To do this, let us imagine that our mile markers are subdivided into more precise markers, such that there is a marker every 10th of a mile. Now we treat the problem the same way we did before.
Because the arrow is moving at a constant velocity, the answer will always be the same. Let us ignore this for a moment, and keep pushing this idea of subdividing the mile markers to finer measurements so that we can make the time interval between measurements smaller and smaller, getting us ever closer to Zeno’s instant in time.
Let’s take a look at our average velocity just before the 1 minute time point and see what we get.
As we make the time between measurements smaller and smaller, the velocity of the arrow doesn’t change. We could take the time between measurements even smaller…in fact we could take them infinitely smaller until the difference is zero, and still get the same velocity. It’s safe to say that the instantaneous velocity of the arrow at the instant in time of 1 minute is 1 mile per minute. Technically, we have solved this paradox. But because the arrow was moving at a constant velocity, the answer is rather obvious. But that’s a good thing; the idea with this exercise was to get you familiar with the concept of the limit.
Taking the Limit
A few of the commenters in our previous article pointed out that the idea of the limit is an important ingredient to The Calculus. I don’t disagree. In our above example, the process of taking finer and finer time measurements is referred to as a “limiting” process. In a real calculus problem, we would limit this value all the way to zero. My idea is to keep things as simple as possible in these articles, so we will not be covering the limit in detail. But it is important to be aware of it. At this point, all you need to understand is that as we take increasingly finer measurements, we converge on a single number. This is the main thought process behind the derivative.
Now, because the arrow was moving at a constant velocity, it made our example almost too simple. To truly understand the derivative and its power, we’re going to have to bump up the complication just a little bit. Let us look at the arrow once again, but this time with the arrow accelerating.
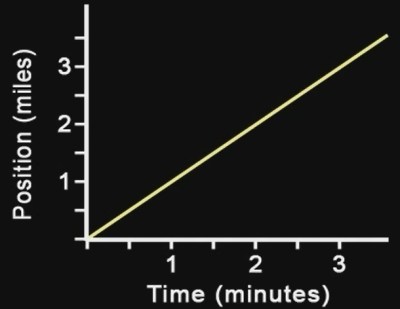
If one were to graph the first example with the arrow moving at a constant velocity, they would get a linear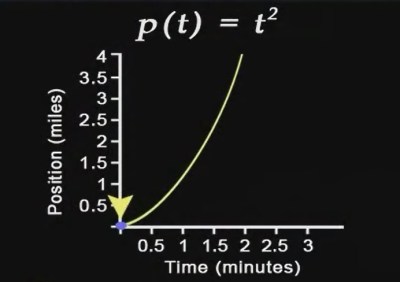 
function of p(t) = t. What this means is that the distance traveled will always be equal to the time. So at any point along the path of the arrow, we can say the elapsed time is equal to the distance traveled. So at the 1 mile marker, we have an elapsed time of 1 minute, 2 minutes to the 2 mile marker, 3 minutes to the 3rd and so forth.
Let us change that function to p(t) = t2. This means after an elapsed time of 1 minute we are at the one mile marker, after 2 minutes we’re at the 4 mile marker, after 3 minutes we’re at the 9 mile marker…you get the point. We’re accelerating. We will apply the same technique of taking the arrow’s position at points in time and calculating its average velocity. Below, we see the average velocity after 1 minute is 3 miles per minute.
And just as before, we will begin to calculate the average velocity through smaller and smaller time intervals trending to the 1 minute time point.
Just as before, we seem to be converging on a single number: 2. And just like before, we can make the time interval between measurements infinitely small…as close as you’d like to 0.0, and we would end up with the value of 2. We can say that the instantaneous velocity of the arrow at a time of 1 minute is 2 miles per minute. We have now truly solved Zeno’s “The Arrow” paradox. The arrow is indeed moving at a known velocity at an instant in time, for we have calculated it. Can you believe it took two thousand years to figure that out!
Making the Derivative
We can all agree that finding the instantaneous velocity through increasingly smaller time intervals is a simple process. We can also agree that it’s a laborious and mundane process. Lest you get disappointed, the derivative has not surfaced just yet. You now know how the derivative works, but you have yet to see its full power. To see this, we will need to perform the above process for other times.
We have proven that the instantaneous velocity of the arrow at the time point of 1 minute is 2 miles per minute. If we wanted, we could go through the tedious process of working out its velocity at other times. But not to worry, I have already done that for you. Below are the instantaneous velocities at time points 0.7, 1.4, 2 and 3 minutes.
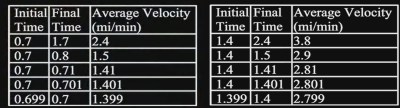
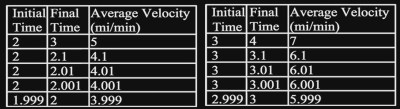
Using the same process as before, we see that we converge on a single value as we take finer and finer measurements. At time 0.7, the average velocity gets closer and closer to the value of 1.4 miles per minute. For time 1.4, the average velocity is clearly 2.8 miles per minute. For the 2 minute mark, it’s 4 miles per minute and for a time of 3 minutes, the arrow is moving at 6 miles per minute. That’s a fast arrow!
The pattern is obvious. The instantaneous velocity is twice the value of our initial time of measurement. We can say that if p(t) = t2, then v(t) = 2t. We can abstract the derivative by saying the derivative of the function f(x) = x2 is 2x. We can also make a generalized definition of the derivative using Zeno’s arrow example:
You should be able to understand this by now. The little pyramid symbol is known as a delta, and just means “a change in.” This equation gives us the average velocity of the arrow. As the delta t becomes smaller, the two positions of the arrow (in the numerator) grow closer together, eventually giving us the instantaneous velocity at time t. The concept of making delta t smaller is what makes the equation a derivative. If you can grasp this concept, give yourself a pat on the back. This is what a student would see in a calc-101 class. Look familiar? And you now know this equation, not by brute force memorization from note cards, or plugging in variables like some data entry clerk, but by a fundamental understanding of how it works. That’s why we’re hackers. That’s how we roll.
There is a lot more to the derivative than what I have presented here, but I hope this article has given you a basic understanding of its underlying concepts. In the next article, we will follow this same process with the integral, which is like an inverted derivative. In fact, you will often hear the integral referred to as an anti-derivative.
Extra Credit
If you feel you’ve mastered the concept of the derivative (within the context of this article), I challenge you to prove it in a language your fellow hackers can understand – code. Consider a machine that measures the volume of a liquid being added to a closed container. It does this by recording the increase in pressure inside the container as the liquid is added, and using Boyle’s Law to calculate the amount. There is a problem, however. Sometimes the liquid runs dry, resulting in air getting into the closed container. The engineer needs to figure out a way to detect this. Because there are thousands of machines in the field, she has to use software to solve the issue.
She figures out that when air gets added to the chamber, the rate of change in the pressure increase is greater than the rate of change when the liquid is added. If she can monitor the rate of change of the pressure increase, she can see the difference between liquid and air, and sound the alarm.
Let us see your pseudo code on how you would solve this problem. Try to use the concept of the derivative to monitor the change in pressure.
Sources
All images are from The Teaching Company course, Lecture 2.
I learned algebra in Calculus. I learned Calculus in Differential Equations. I learned Differential Equations in Circuits I and II. The entire time professional engineers kept telling me, “You’re never going to use that again.”
I find personal satisfaction in learning about and understanding advance concepts. I took Calculus in High School and you’re right, I didn’t use it again. But I still enjoyed challenging myself with things like Project Euler and through articles on individual topics like this one.
Nice work Will!
The advanced mathematics are intended to thin the herd(https://en.wikipedia.org/wiki/Cooling_out) and elevate salaries by reducing competition for jobs. Most people can’t hack Calc + Diff Eq’s so they change majors to something that pays less like Espresso Manufacturing with a minor in Gender Studies.
Hardly. It helps having a grounding knowledge in advanced maths to know when the computer software spits out garbage because you fat fingered the inputs in before you hit calculate.
That’s the sad part really. We don’t actually use this stuff day to day, and now we’re teaching people that they’ll never use it, so they never learn it, and then they lack basic understanding of what makes sense when they do their professional work.
I agree with this somewhat. I have a professor that describes the undergrad curriculum as “preparation for graduate research” as opposed to “preparation to apply technology in the field.” It should be noted that if you’ve ever summed a series of integers, you’ve “done calculus.”
So by extension, you should also have knowledge of computer programming to …. you get the idea. Where do you stop? At some point in time you have to say ‘I can’t know it all and have to limit my focus’.
Well aren’t you cynical? What you say might be true if your career path is purely digital electronics and you stay in the abstract realm, eg, you never have to design a PCB or consider edge rates or instantaneous current when designing a chip. But there are many opportunities for calculus in most EEs lives.
Even if you never have to formally sit down and write down the Fourier Series expansion of some signal, the intuition one develops and the flexible way of thinking about time and frequency is invaluable.
god, i’ve heard the “you won’t use *this*, ever again”. You don’t learn PDEs or integration because at some point you’re going to have to calculate a definite integral to save a leg or your first child. You learn math (arithmetic, algebra, calculus, etc) because practicing math sharpens your brain. You give your brain extra tools with which to approach problems. It’s not like basic reading where you learn reading so that you can *read*, it’s like physical education. You don’t do physical education because at some point in your life you will need to run around in circles, but because by exercising you prepare your body for future challenges.
This bit of wisdom can be used everywhere.
Understanding calculus also reduces what you need to commit to memory. eg: Area of a circle and circumference of a circle = two equations, with calculus you only need to remember one of those, the other is obvious.
In fact, you can get both of these from calculus:
The equation in polar coordinates for a circle:
f(phi)=R
And so, the integral looks like this for circumference:
integral phi=0…2*pi (f(phi)) = integral phi=0…2*pi (R) = 2*pi*R
And area:
integral R=0..R (2*pi*R)= pi*R^2
Still don’t get it. Yes, I’m stupid, retarded, whatever adjective you wish to use.
I doubt you are any of those things. Learning takes time and the explanation may need to come from a different vector. Try Googling around to get some different styles of explanation and I bet the meaning will slam into place for you.
The thing about teaching is that every student knows a different subset of what you’re trying to teach. I have never once come across someone teaching calculus in a book or a blog that has correctly assumed what I know and don’t know. There is always some more fundamental building block that is assumed known by the reader/student, and I’ve not yet been able to learn it.
given that everyone I know learned, understands, and uses calculus quite easily, I must assume that I am… “slow.” All the evidence available to me points toward it.
You shouldn’t feel that slow if it took all of human history till Newton to find this out. But as a 33 year old in the middle of taking 3 years to finish community college I feel the same way VERY often.
I am in calculus now, and oftentimes some kid will say something and the teacher and he will have a dialogue about whats being taught, and its almost always over my head. Once in a great while I will say something or ask something and everyone will look at me like I grew two heads, because they all feel the same way, they have no idea what they are learning and now they think I know what is going on, but I don’t..
Calc 1 was about memorizing the common derivatives (or using a cheatsheet) and finding ways to manipulate equations until they looked like something that was recognizable on your cheatsheet and then applying the derivative that is on the cheatsheet. I had no idea what was going on.
Calc 2 was about doing the opposite to derivatives (the anti-derivative). I began to understand calc one here, and had a very loose understanding of what I was currently learning, I just tried to memorize what I could for good grades.
Calc 3? I’ll let you know after my summer class.
Like one of these calc articles said, the whole textbook is two concepts and 998 examples of those two concepts, but with an added two pages of cheatsheets of common forms to apply the two concepts to save you a bunch of work. It’s just another tool like multiplication and division, except it involves unsolved variables. I F’ing hate it, because it’s too theoretical for me to easily understand, but I can see how useful it is, even though I think 90% of my fellow engineering students, don’t know why they are learning it, or what to do with it.
I like practical subjects like physics, they are intuitive to me, but remember that Carl Sagan was such a good teacher because he had such a hard time understanding the subject, and I don’t think Sagan was slow.
I feel like the Idea that everyone can learn everything is one of education’s biggest blunders, the idea that any one brain and body have the ability to both learn, understand and succeed in all/any discipline is really aqward (I’m leaving in the spelling mistake) and results in this article, which doesn’t make me want to lean, it makes me feel like an idiot because “oh its really so simple” its not to some people because people can think completely differently, no one does this for languages except for a select few who are almost immediately told, “hey you have an ability in language learning. it ussually isn’t that easy” Its not easy for me, i hate when someone says something is easy flat and simple, nothing is flat and simple ‘ever’ easy or hard. like I’m good at psychology, but absolute garbage at about everything else (I’m ok in band and bio but photosynthesis and cellular respiration kill me). I can agree that yes with enough time and explanation it can be learned, but i don’t think some take into account that might be at least a day for one subject or one part of a subject.
(not addressed to you Mike):
To those who argue that it helps sharpen the mind, just like PE sharpens the body, you can’t sharpen a blade if your whetstone is at the wrong angle, in other words, If i don’t learn the info, or if i do the exercise wrong i dont sharpen anything, i might do nothing or dull my self.
The ‘derivative’ of a function is an equation which tells you the slope of that function’s curve at any point.
A ‘slope’ is the ratio of the change in y to the change in x.
To more accurately get the slope of a curve at a point, you’d want to measure the tiniest change in y caused by the tiniest change in x and calculate that ratio.
Say y = 3×2 + 4, just to slightly change the example. How in the world do you get the slope at a point? You try to figure out that ratio of vanishingly small changes, which are written as dy and dx.
If y = 3×2 + 4 then y + dy = 3(x + dx)2 + 4. Multiply it out and you get
y + dy = 3×2 + 6xdx + (dx)2 + 4. Well, that made a mess!
But you know that y = 3×2 + 4, so you can simplify to
y + dy = y + 6xdx + (dx)2 and then further to
dy = 6xdx + (dx)2. Now comes the trick: if dx is vanishingly small, say, a jillionth of an inch (or 2.54E-42 hm) then (dx)2 is a bazillionth of a square inch (or 6.4516E-84 ha). That’s nothing, toss it!
So, dy = 6xdx and then dy/dx = 6x. The slope of y = 3×2 + 4 at any point is 6x.
That’s just the source of all the patterns people use for derivatives. In real life, you see x3/4 and you go, ah- (3/4)x2.
Well, the superscript tag didn’t work, so the preceding is useless. Sorry about that.
Wait… liquids are incompressible. The rate of pressure change per volume should be higher for liquids than for air, shouldn’t it?
The pressure he’s talking about, I think, is the pressure at the base of the container. Or in other words the weight of the water.
If the incoming pipe is constantly providing water, then the tank’s fullness will increase at a certain rate. If some air gets in, that rate will be different. Your job is to calculate the rate for constant water, then have the program complain if it doesn’t match reality. I think.
Pretty sure I understand that. This calculus is still going over my head though. Some things are easier with a human you can ask questions of, interactive. I think I understand it better now than I did before though. It’ll click, eventually.
Great article! Hate to be THAT guy, but velocity is a vector is a vector, whereas speed is a scalar, with no direction component. For the purposes of the “arrow” thout experiment, speed is the correct terminology, not velocity.
Is it really though? Because the angle does matter in this case. The Arrow must travel in a straight line that passes each point. If it were going off at an angle toward or away from the observer, the speed measurements from their perspective could be the same as discussed in this article. But the actual speed of the arrow at any given instant would be different from what the observer perceived.
Yes, it mattters. Within the inertial frame of reference, that of an outside observerver, it is only scalar speed. Mike, you are putting yourself inside the inertial frame of reference
Bloody hell, it’s an imaginary arrow travelling in a straight line. People are trying to learn, here!
Velocity is a vector containing a direction component. “The arrow” thought experiment is actually referring to the scalar speed. Nitpicky, i know, but when talking about math precision of terminlogy is important
In case anyone is wondering this is the order schools typically teach math in any part of the world: pre alg>alg i>alg ii>calc i>calc ii>calc iii>calc iv>DE>linear alg
Algebra is pretty much where all the advanced stuff lies. Topology is built on it. If you’re in algebraic topology or abstract algebra you’re pretty much at the top and only have theory to explore.
Funny thing is engineering math isn’t really hard math. You’ll see once you get past DE.
You guys take DE before LinAlg!? That makes no sense, the only thing Linear Algebra was ever useful for me was for solving DEs, why would you learn it after having to use it?
I assume you were looking for eigenvalues/eigenvectors. LA is the basis for the algebraic description of geometry and algebraic proofs of geometric theorems. Also, linear programming for optimization, transformations in the plane and in space as in computer graphics.
I recall taking linear before DEQ or perhaps simultaneously. In physics, you take a lot of it in the math department and do it again in physics classes like eigenvectors in mechanics and differential geometry for general relativity and gravitation. A linear algebra course just touches on the eigenvalue problem since there such a vast amount of other stuff in linear algebra.
Yup. Eigenpairs for system of ODEs were the first actual use I saw for LinAlg. Later on I heard about other uses, I think I friend of mine had a lot of it for description of quantum chemistry phenomena during his PhD research, but the only uses I bothered studying were the applications in ODE and PDEs solutions.
?! The math after diifferential equations- which I loved- was partial differential equations. They killed me. That kept me out of fluid dynamics.
Yeah DE is the hardest at most schools, but what comes after DE and linear algebra makes you feel like you’re just starting.. Abstract-algebra is the one that kills math prodigies and is only trumped by things in number theory..
By the way calculus is just the fun stuff before math gets hard. It’s really cool when you use it in economics and basic physics and statistics.. It’s where most people stop with math too.
Partial DEQ is hard for everyone. There are no clear methods or tools (like the guesswork needed in DEQ but much more so). Grind through a Frobenius solution or ? I used a shortcut a lot. The school had an old analog computer from Beckman and I got it working (this was before – gulp – everyone had access to computers) and ran time-dependent parts of problems then looked through Abramowitz and Hill for similar looking curves. I hit more often than I missed.
That was before I realized nearly all textbook problems have symmetries and and geometries that make them work out nicely. Many will yield to a thought experiment or logic of the sort “If it isn’t A, what would that mean?” The excellent E&M book by Griffith is like that (spoiler for students :-) and you can do all the problems without putting pencil to paper. Don’t tell!
What about geometry and trigonometry?
” pre alg>alg i>alg ii>calc i>calc ii>calc iii>calc iv>DE>linear alg”
Can you write that in English please.
More often. Pre-Algebra, Algebra, Calculus, DEQ, Linear. [should include multi-variate or advanced calculus and abstract algebra]. Where DEQ is Differential Equations or equations based on small differences in quantities and their relationships, like ratio. The 1 2 3 i ii iii iv are quarters or semesters or someone’s idea of a logical break in the development of the material. It all looks rather intimidating but might be better off without the divisions since they blend together, but public school attempts to build continuous or circular curriculums have been dismal failures and forced the colleges to provide remedial math.
So presumably it’s some sort of list dictating the order in which these things are taught in America. Are they the names Americans give them? Is “pre-algebra” arithmetic?
In the UK when I was at school calculus was taught quite early on (12 -14 yrs) but no explanations, just tables of standard derivatives and integrals and I never knew any more than that until I learned Laplace and got to the proper root of such things.
I do find it irritating that mathematics and arithmetic are mixed up, it’s like saying “I am spelling a book” instead of “I am writing a book”.
Pre-algebra is an introduction of abstraction without diving into proofs. It reviews (or introduces) arithmetic ideas about using decimal places correctly, number lines. intergers, whole numbers, real numbers, points, points in the plane and coordinate geometry, slopes of straight lines, and the areas of geometric objects that can be determined without algebra but can be proven with geometry. Plus other stuff.
I know, it could all be part of an algebra book if the modern books were not huge and filled with pictures and junk in the the extra wide margins. My grandfather’s algebra book from high school in 1890 is quite small, succinct, and complete with plenty of figures (which are not huge). And it includes most of pre-algebra or simply doesn’t need it because he leaned it from an equally small and complete geometry book – which included a lot of very practical applications.
The assumption by authors of the times were that the student would move on to build a business or become a craftsman so the book’s emphasis was on that. Today the books and the problems assume you either work for the government or need to calculate the taxes automatically paid by your employer. The student is never the company owner unless it is a team activity like a bake sale. Don’t look at a contemporary US high school math book unless you want to be really really disappointed.
We did differential equations at school. You draw a graph, right? Or rather two graphs, and find where they cross. Also did some reasonable amount of algebra, and some geometry I’ve forgotten, but figured out by bungling with code that you can draw a circle in Cartesian coordinates with sin and cos, multiplied by the radius. Sine waves pop up a lot in real life and are something to do with the circleness of a circle.
Didn’t do Calculus though.
Actually learning calculus and advanced math concepts add tools to your though processes that
you use unconsciously. Knowing about derivatives and integrals and statistics enables a more
insightful view on problems.
Nassim Taleb says
Mathematics is for contemplation not calculation.
wow, i am surprised that i had to search so hard to find the right answer, especially among present company.
you win!
Actually along those lines, cellular automata are a great demonstration of chaos theory that you can put your hands into. Chaos theory explains so many things in the Universe that other explanations don’t. Once you know the principle, you start recognising it everywhere.
Thanks for another great article Will – I’m liking these a lot.
@naikrovek – I can empathise with your “not getting it”, as I find it hard to retain abstract math rules, too. I think Mike’s advice could be good, as in my day job as a programmer I have ‘invented’ the Newton Raphson interpolation method (APR calculations for mortgages) and integration (calculating gas flow volumes per unit time from time series as spot readings). Of course being as thick as pig er, mud, I didn’t know it at the time.
I’ve been reading the book mentioned in the comments from last time, “Calculus Made Easy” (from the year 1914!). The title doesn’t lie. Never realized how easy derivatives could be.
I ruined many an engineering coworker’s productivity (and my own) last week with that book. Love it.
It’s been about 7 years since I studied calculus as part of my EE degree so I’m quite enjoying this series of articles as a bit of a refresher!
Well it is 25 years since I did it and I find it depressing that I am having to think about things that I completely understood and took for granted. :(
If you are going all math/science etc please use SI units instead of pounds stones mi mil feet etc
m/s is the unit you want, mi/min is 1 609.344m/min :o
1feet = https://en.wikipedia.org/wiki/Foot_(unit) what foot? indian? us? survey this that?
Exactly! SI is not hard.
neither are any other arbitrary unit systems.
True. As long as it’s just miles, it’s just as simple as km. There’s no super-unit of miles that you have to divide by 27 to get, like there is with pounds, ounces, stones. Miles are just miles. The examples would still work in furlongs, poles, or cubits.
+1
Maybe we need a post on arithmetic.
Noted. The next articles will be in SI units. These are based off some The Teaching Company lectures, and they used miles/minute in them. But it’s easy to change.
Lets not abandon tradition! A mile is a great unit. 1000 strides for a Roman soldier (1M strides). Average today is still between a 5 and 6 foot stride (say left foot to left foot) when marching or hiking. Even better, some hacker should find a cool way to make surveyors measuring chains like use to map India! That would be cool.
Mixing / converting units really isn’t that hard, and is a useful skill to have.
I’m an (American) engineer working for a European company here in the States, and (while I prefer SI) mixed units are simply a fact of life.
yes… it would be nice if we converted to all SI, but let’s face it, that would take an act of Congress (tried and failed in the 1970’s). We probably won’t convert to only metric until the rest of the world converts to only English. Until then, I expect to have to convert units on a regular basis.
I use and convert between SAE and metric every day at work, and every evening in my sport. Many years ago, we did that all thru college, too. I enjoy it, but I like speaking other languages, too, so I might be an oddball.
Amazingly ovious way to spell that word! :-)
Fixed. THanks!
So lots of comments but didn’t spot anyone doing the homework.
Lets see, click the link, read up on Boyles law. A little insight gained.
So assuming temperature is held constant we want too:
Measure pressure against time.
Made up code follows:
>float pres = 0; //pressure reading value
>float oldpres = 0; // stores old pressure value to compare against
>float increaselimit = 2; // arbitrary increase limit chosen
>
>//initialise readings
>pres = read(pressuresensorpin);
>oldpres = pres;
>
>loop
> pres = read(pressuresensorpin);
> if pres > oldpres then //pressure is increasing, this is what we expect
> if (pres – oldpres) > increaselimit then //pressure is increasing faster than expected
> print(“increase too fast, gas in system, liquid ran dry”);
> else
> print(“liquid entering system at expected rate”)l
> float rate = (pres – oldpres); // gives pressure increase per millisecond
> rate = rate * 1000; //g gives pres increase per second
> print(rate);
> else //pressure is dropping, erroneous behavious
> print(“pressure drop error detected”);
> end if
> wait 1; // milliseconds
>end loop
This probably isn’t right. Please help me improve it.
doh none of the indenting worked making this barely readable. Fail :(
All of the above is intuitive to the most casual observer and will be left as a simple student exercise. Yeh, right…
Calculus is not an easy subject for me. I’m a non-traditional student that started college at age 24, not 18. Because of the difference in years I haven’t done Algebra and Trigonometry for years.
The high-school I went to basically threw home-school videos at us, and as a result, was sub-par in standard. There were no tutors available in-person to ask for help for questions. Parents didn’t understand how to solve the problems. I was left with a weak foundation as a result of these actions.
Enter college 8 years later after a hiatus due to financial hardships, I’ve attended a 4 year. One of the requirements for my degree is this subject. I’ve managed to pass the first test by a miracle but only literally 1 point away from failing. The second test ended up being 5 points below the first.
Each question is worth either 15 or 20 points. Get 1 step wrong, and the entire question is a 0. Test are always purposely vague in a way that professors refuse to tell students what will be on the test except the generic “Chapter x is on the test” routine. They have become so obsessed over plagiarism/cheating that they refuse to provide information what’s needed to pass the course. That’s like purchasing a certification-prep course and then being told by the prep-manufacture “Well, we don’t know exactly what sections will be on there, so we’ll just throw the entire book at you. Good luck figuring it out”. Real certification courses do not do this. They do indeed teach the material needed to ace the tests. All of our math tests have always be in-person with no devices, so the entirety of a student “cheating” is thrown out the window.
I have told my professors these issues, but they have failed to accommodate the courses. On-top of that, I also have a medical condition that can affect my brain’s retention that did not occur until my later years of life, and at anytime can relapse. It is not ADHD but symptom. As a student you are taking multiple classes, not just 1 or 2 subjects. Multiple courses means more time spent studying and preparing for those courses. The fact that even some professors “expect” you to know this material off the top of your head like someone that just came out of high-school is very ridiculous and borderline unfair. Students of all different life come to college, not just the young. Sometimes I would ask a question where a particular part of a problem came from, and the professor(s) would act like it was a nuisance to ask. It gave the perspective as if, by even asking to verify the material, that I was “stupid” for not remembering it.
The reality of it all a lot of professors really don’t care about this. Their stuck in their ways and have taken these classes long time ago when circumstances weren’t an issue. They went to a school where there was support be it from a parent paying tutoring for them, or having a teacher assist them.
The college that I go to recently decided that students using “walk-in” hours is too available. In other words, they are literally restricting students ability to get help in subjects based on perceived nonsense such as “dependency” or “monopoly”, and that tutoring shouldn’t be a “study-hall”. Each and every-time these poor excuses are used to create road-blocks in student success, “hours” are delegated. As a result, its the college that is micro-managing students to 1 hour an entire week for tutoring. Putting restraints on students ability to get help for courses they are paying $1,000 or up for creates unnecessary burdens and roadblocks for the students. When no students use the walk-in hours, tutors sit there practically for 3-4 with no students. This is a resource waste. Math professors have been known to load up 20 questions per chapter for subjects, which is always due in 2 days. That is not enough time to understand everything in less than 1 hour per week. As a result, it creates an unfair obstacle and burden to the student.
The students that are being affected by this are students like me. These issues have been recent since our last semester, and many students that are struggling are either non-traditional students like myself, or students that have disabilities. We have an authoritative tutor director who is deciding what a student needs, despite that each student is paying tuition, and that each student has the right to a decision decide how much help they need for a subject in their own discretion.
It’s why I’ve been using third-party services for tutoring, that don’t have the school’s administration involved restricting and “keeping a paper-trail” on students using the tutoring services. It’s disgusting I am paying nearly 60k in debt to attend college, yet I can’t even access a resource because an administration person believes that students are “gouging” the tutoring center for walk-ins.
I’ve been forced to re-take calculus because of these issues being created mainly by administration. As a result, my graduation got delayed, and I ended up having to pay additional money for a course that I should not have had to re-take. For 3 weeks since the start of the semester, there has been no tutoring available. It wasn’t until 3 days before a test walk-in hours became available. I’ve put in a request for tutoring earlier the semester, and it was delayed for weeks until finally I got 1 tutor. Unfortunately, that tutor couldn’t be available for a 1 on 1 afterwards.
The administration also has set up for the tutors to actively “report” the students. In other words, Compass is used as a reporting/negative tool about student’s progress. Many of the tutors who tutor are Sophomore and Freshman, and many of them lack the maturity that an older student would have. I had one such tutor call herself “reporting” me simply because I asked if the steps could be done more through at the end.
What was not considered was my age gap, medical disability, and the overburden work-load of having assignments due literally in 2 days everyday of 20 problems per section or receive a 0. Imagine trying to fit all of that into your schedule, on top of other classes.
If anything, the academic institution that I’ve been attending has left a bad impression and it’s faults is an obvious and distinctively unfair disadvantage to people like me. I am paying money to a school that refuses to help me learn, and as a result, get “punished” when I seek help by having tutors either report me for minuscule things such as a question, or an aggressive administration that is more interested in limiting the available hours for students to use than the progress of what the student needs for a class.