The Fourier transform underpins so much of our technological lives, in most cases probably without our realising it. The ability to mathematically split a waveform into its frequency components and vice versa underpins much of the field of digital signal processing, and DSP has become an essential part of many electronic devices we take for granted.
But while most of us will know what a Fourier transform is, fewer of us will know anything of how one works. They are a function called from a library rather than performed in themselves. Even when they are taught in schools or university courses they remain something that not all students “get”, and woe betide you if (as your scribe did) you have a sub-par maths lecturer.
The video below the break then is very much worth a look if Fourier transforms are a bit of a mystery to you. In it [Grant Sanderson] explains them through a series of simple graphical examples in a style that perhaps may chalk-and-talk mathematics teachers should emulate. You may still only use Foruier transforms through a library, but after watching this video perhaps some of their mysteries will be revealed.
The occasional mathematical piece makes it way onto these pages, in the past we’ve brought you an examination of the same process when summing sine waves.
Via Hacker News.

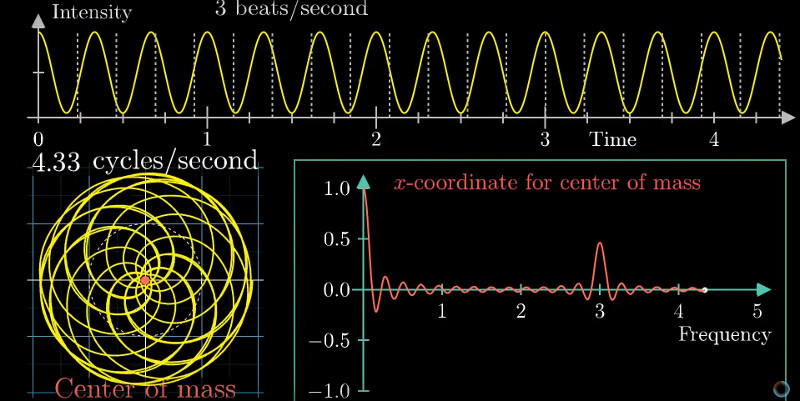














Our linear algebra professor explained the Fourier transform to us in our first year as a base transform of the complex function space with a special orthogonal base. After she had written those three lines to the blackboard, she went on with another base transform example.
It being defined like that really helped a few years later when the Fourier transform was introduced as a tool in the signal processing lecture.
I have a midterm exam on exactly this tomorrow!
This is one of the best channels on youtube. Every time I watch one of his videos, I find myself considering going back to school to get a degree in math.
Unfortunately not as much money in it. Great as an underpinning for everything else.
I never considered money when enrolling for a degree. I despise the idea even. Learn something out of passion or get lost.
That might happen if you study in the wrong country.
At our local university it’s currently 1674€ a year if you take too long to get your degree and only 674€ a year if you are still in time.
LOL, I have no passion for anything. Sadly I have to live so I became an engineer. If I’d have taken your advice I’d be a bigger drain on society than all those people getting degrees in subjects that have no job prospects.
I envy people as ignorant and arrogant as you.
Unfortunately for you that either reads as, “I’m not the one paying for my education”, or “I’m stinking rich, I don’t have to worry about money”. Nice if you can get it, but for the real world people we owe money to don’t accept “passion” as a form of payment. In other words WE do have to worry about our profession generating an income and hence what degrees we go for.
Right… or the objective becomes “Hunt the Wumpus” for real strange different crazy subsidized (thankfully was making ~$75K and billions, if not millions) disabled not overpaid ineffective intentional false pretense trying to look and act official.
I knew a guy who got his degree in English and made more money mowing grass. Whats the point of getting a degree (and possibly getting into a large debt) if you can’t make a living wage with your “passion” based degree? That seems like it should be a hobby at that point.
Nice description. When I took the signals classes in my undergrad EE curriculum, I was always frustrated by the Fourier transform- actually doing it, got even more frustrated when I got to Laplace transforms and how it was useful, but then in a graduate DSP class the z transform (the discrete time version of the Laplace) is what made it all fit together. While it is a pretty specialized path to go down, I hope 3Blue1Brown will get to a discussion of the z- that’s where shit gets done!
The Z-Transform should ALWAYS be discussed in parallel with (if not soon after) an introduction to Linear Time-Invariant (LTI) Systems! This is especially true today where digital signal processing is so important. But that’s still not the way it is done in the formal University system. Much of the problem has to do with the horrible way hugely over-priced university-level text books are sold and controlled. Online education CAN help with this problem, but in most-part the online content does NOT deviate. Online content still tries to mirror the broken and out of date in-classroom practices in formal university systems. Case in-point is this video introduction to the Fourier Transform.
The best explanation of Fourier transfort I have seen yet.
This channel as also video exposing backpropagation calculus used in artificial intelligence. Excellent channel.
“The ability to mathematically split a waveform into its frequency components”
That is incorrect.
Waveforms are not made up as a series of sine waves, waveforms can be represented as a series of sine waves. Waveforms can just as easily be represented as a series of square waves or triangular waves or any periodic waveform you care to use.
Sine waves are easy, that is why we use them but making the statement that all waveforms ARE a series of sine waves leads to confusion..
Is this useful for modeling anything or just semantics?
Just semantics. The sine wave is the simplest one, containing the least amount of information. It’s spectrum consists of just one frequency component, so it’s natural to consider other waveforms to consist of sine waves rather than the other way around.
Of course you can construct any waveform by combining any other waveforms, but when you actually do the math, you find that you’re really adding and subtracting sine waves.
For example, the continuous mathematical expression for a square wave is:
https://wikimedia.org/api/rest_v1/media/math/render/svg/0bcc48dbe98962e42f637f24dcaf4ecd71bd2af5
Which is an sum of an infinite number of sine waves.
+1
Good explanation. I’d add that I say “this force is a vector,” what’s the point of arguing that the force isn’t REALLY a vector, we just represent it as one mathematically? It’s a pointless philosophical debate.
Look into Walsh Functions, which use rectangular waveforms and can be used to produce audio.
https://en.wikipedia.org/wiki/Walsh_function
Thank you, sounds interesting. I’ll check it out!
Pun intended?
If TGT’s first name is “Joe”, then I’d say “seems to me, pun intended”.
;-)
More specifically, look at the article “Walsh Functions: A Digital Fourier Series” in the Sept. 1977 BYTE magazine (also reprinted in The BYTE Book of Computer Music). In it, he simulates a sine wave using simple digital logic and some carefully calculated resistor values. Both the article and the book are available online.
@rsmilward said:
“More specifically, look at the article “Walsh Functions: A Digital Fourier Series” in the Sept. 1977 BYTE magazine (also reprinted in The BYTE Book of Computer Music).”
And here are the missing links (if the HaD post Editor doesn’t mangle them):
WALSH FUNCTIONS – DIGITAL FOURIER SERIES, Byte Magazine Volume 02 Number 09 – Music and Computers, Sept. 1977, Pg.-190 WALSH FUNCTIONS: A DIGITAL FOURIER SERIES, Author: Jacoby:
https://archive.org/details/byte-magazine-1977-09
.pdf download, 137MB (other formats incl. epub available at link above):
https://archive.org/download/byte-magazine-1977-09/1977_09_BYTE_02-09_Music_and_Computers.pdf
There is no difference between saying it can be represented by a series of sine waves and saying it can be split into its frequency components. In fact, the second is a clearer description when one considers possible signal processing. Nothing said about square waves or triangular waves contradicts that. If it looks like a duck and walks like a duck, it is a duck. (And that does not exclude it at the same time being something else.)
The sentence you quoted doesn’t refer to sine waves. It says “frequency components” which could refer to the frequency of any periodic waveform, including the others you mentioned. Why are you objecting to a statement the writer doesn’t make?
Can’t agree. “Frequency components” are those shown on a frequency versus amplitude plot, and those are sines. You can’t get any simpler or more complete.
Oh dear, an entire career using Fourier transforms to split waveforms into frequency components was based upon a lie told to me during my electronic engineering degree course. Whatever shall I do!
Most mathematical and scientific concepts have several layers of lies-to-the-children. Newton’s Laws to explain All Of Physics, for example. Good enough to explain most things and allow you to do your stuff. That there are more advanced explanations for more advanced learners doesn’t change their ability to be useful at the level they are used.
Well said! ????
I agree 100%
+1
This is why I never ever ever ask anything on HaD. It is best to make humorous declarative statements of little to no value and move on.
*pats nopmataru on the shoulder* We’ll make a politician out of you yet.
Not to worry. Whatever topic anyone brings up, there will always be some smarty-pants who throws a metaphoric Cherry bomb into the metaphoric fire, telling everyone else why they’re all wrong. Ever hear the claim “Scientists say bumblebees can’t fly”?
It’s just an attention-getter, with no other redeeming virtue.
I know the HaD.io environment is a little more supportive, but the main site’s user comments are not. at. all. After getting linked around 10 years ago, I always make sure to hide my published work on private forums (which are generally more supportive imho). But that is not what I come to HaD for these days anyway. I like the random fun read and learning a thing or two and seeing how fragile a person’s ego becomes after a 75k degree. I honestly feel bad for some of the folks that get linked without their knowledge on here and seeing them pop up in the comments. Oh well.
Not true, since a square wave in itself is an infinite sum of sine wave. On the other hand a sine wave can’t be represented by a sum of terms of trigonometric functions.
I should have written, purist mathematicians: unless all the terms of the serie cancel each other except for a single term.
@John,
Using a set of waveform generators outputting square waves of related harmonics. Then using a summing circuit try to generate a signal that look like a sine wave with it. Good luck!
You need to look up ‘orthogonal set’ sometime: https://www.youtube.com/watch?v=2HLXLjvtCZ8
Not just any series of periodic functions will do. First they have to be linearly independent. And if you to be able to calculate the coefficients easily then they need to be orthogonal to each other.
“Waveforms can just as easily be represented as a series of square waves or triangular waves or any periodic waveform you care to use.”
Not really. I’m just a EE, not a mathematician, so my explanation will probably imprecise, but I’ll try.
Even if you used only sine waves of arbitrary frequency it would not be sufficient. That is why you also need to extract the phase or, equivalently, extract the cosine series as well. Without both, there are real waveforms that can’t be decomposed/reconstructed from that basis set. The most trivial example: if you have only sin waves and no phase information to work with, and your function is nonzero at x=0, it is impossible to represent because no matter which weighting of the sine waves you used because each one is zero at x=0.
The real requirement is that whatever function set you are using, they need to for a complete basis. The fact that sin functions are all mutually orthogonal means that there is a unique representation, which is useful.
yes, its all about having a basis of orthogonal functions. I was taught the fourier transform through linear algebra, where functions were just the logical conclusion to vectors, this seemed to make it all easier to understand than when I was taught it in calculus
WONDERFUL!!!! Many years ago, my major professor asked me to look at how we could use a computer to explain knotty concepts in math. Like, for example, how the derivative of a function derives from a divided difference, as time interval shrinks to zero.
We’re talking about the 50’s here, so we’d have to create a movie rather than an interactive graphics display.
But this tutorial proves beyond a shadow of a doubt that the technology my prof dreamed of has arrived. I am _SO_ impressed!!
Nice video. Why all the pedants saying its incorrect to say you can split out the frequency components? It’s a great tool for doing exactly that.
I studied maths and electronics for 4 years as then worked in this field for 15 years designing vector signal test equipment
When you truly understand it you won’t be offended by these types of explanations.
https://www.smbc-comics.com/comics/20130201.gif
I think he was my math teacher in high school.
Great visual representation of the graphical data in qualitative and simple quantitative ways. The best video detail I’ve watched so far on FT’s. Even better can be elaborating on the various types of FT’s. I was thinking Jerobeam Fenderson “Oscilloscope Music Tutorial 4” was the best I’ve watched for explaining visually really basic sine and cosine waves, though he is only going into phase of a sine and cosine wave.
This is really nice. How are the graphics done?
One common way to look at the FT has been as a collection (infinite collection) of correlations of the signal of interest with the individual spectral frequencies. Then the DFT is a finite collection of components you intend to use or plot. IIRC the first big applications for FT were in Quantum Mechanics, then in optics and synthetic aperture systems. (That’s aside from much earlier applications in the theory of differential equations.) Now it is used in everything from medical imaging to radio.
This visualization from 3Blue1Brown with the circle spinning term and the vector magnitude term (and phase) I think is really much better for communications and SDR and all kinds of signal processing. In SDR the square wave switching method of detection is amazing, and watching a HackRF on the computer I have doing super smooth 64K DFT is pretty dang mind boggling. It all uses these concepts, often reduced to crazy simple hardware. This FT visualization should make understanding how this all works much more accessible. It would be great to follow up on how many people make a personal math breakthrough as a result.
Now I have to watch all the videos.
IMHO, this is the most interesting thing ever published on HaD (and I’ve been around a while). Now I’m off to find a way to also make it the most useful (by using it to perfect cold fusion or something).
nice explanation as always. i’m amazed how fourier transform works, so i tried to understand it. the easiest way to is to make your own explanation. this is what i made in 2D: https://youtu.be/_wKpKePKoDg
better to watch on non-mobile devices because of youtube’s annotations.