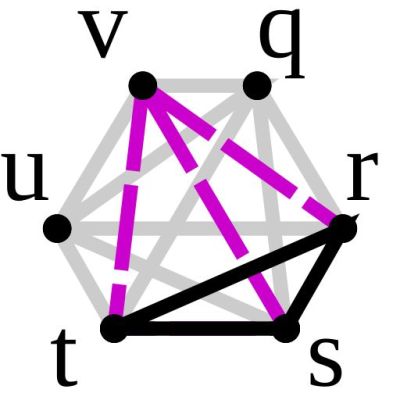
Generally when assuming a chaotic (i.e. random) system like an undirected graph, we assume that if we start coloring these (i.e. assign values) with two colors no real pattern emerges. Yet it’s been proven that if you have a graph with a certain set of vertices, coloring the resulting lines in this manner will always result in a clique forming. This phenomenon has been investigated for nearly a century now after its discovery by British mathematician [Frank P. Ramsey].
The initial discovery concerned a graph with 6 vertices, providing the lowest number of vertices required. Formally this is written as R(3, 3), with subsequent cases of these Ramsey numbers discovered. They are part of Ramsey theory, which concerns itself with the question of what the underlying properties are that cause this apparent order to appear, which requires us to discover more cases.
Finding the number for a particular instance of R(m, n) can be done the traditional way, or brute-forcing it computationally. Over the decades more advanced algorithms have been developed to help with the search, and people from different fields are mingling as they are drawn to this problem. So far the pay-off of this search are these algorithms, the friendships created and perhaps one day a deep insight in the causes behind this phenomenon that may have implications for physics, chemistry and other fields.















Perhaps we will discover a message in the pattern that instructs us to build a device that will permit a traveler to go through a wormhole to another star system to initiate contact with an alien species………..
No! Go home, Jodie Foster!
Be careful what you wish for…:-)
“A is for Andromeda”
Is chaotic not a different thing than/from/to random?
(above was meant to be a standalone reply)
Yes. Chaotic systems are fully deterministic, but are not differentiable at any point. Random systems are non-deterministic.
We arrive and one of the aliens rolls all 7 eyes and say ” oh great the Earth hillbillies are here…”
This is melting my brain and the links don’t seem to have more illustrations.
Is it saying that if you have enough random things invariably there will be patterns apparently?
Kind of like if you have enough random people they might end up being family members? Or even groups of fans of the rock band Ghost?
Honestly I couldn’t follow this article at all, so I went to Wikipedia to look up the information.
I couldn’t follow Wikipedia, either, lol! Math is not my strong suit. Theoretical math even less so.
This video has a nice introduction to the general topic: https://www.youtube.com/watch?v=ZykdsnIpXNk
Agreed
Yes
Yes
It’s random so it works, right? The telltale sign is that it’s the reader that give these things significance. Keep this in mind when reading stock charts.
I seem to have stumbled upon Mathaday. ;)
When reading math articles on Wikipedia, I change the language to “Simple English”, otherwise it’s all written in code. If only there was a similar dropdown here…
Ley Lines for the mathematically inclined?
I was with you all the way up until “undirected graph”.
I need to do some reading.
It’s been a while, but from what I remember, a directed graph is where you’ve a one-way system. You can move a line in the directions of the arrows only.
With an undirected graph, you can move in either direction along any line.
Goddam Hackadoodle! Define your terms! What the heck is clique? The reader should not have to research that.
It seems to be a group that’s statistically significantly connected to eachother and also statistically significantly disconnected to the rest of a set of something.
From what I can gather, a “clique” is a complete graph (a set of vertices where every vertex is connected by edges to every other vertex) that is part of a bigger graph (a set of vertices where each vertex is not necessarily connected to any other vertex.) Here, the big graph is also a complete graph and we’re coloring all of the edges of the big graph with two different colors and only considering cliques where every edge has the same color.
Given that, my understanding is that when you have a complete graph with the Ramsey number R(m,n) number of vertices or more, no matter how you assign one of two colors to every edge, there will be at least one clique with m vertices of one color and at least one clique with n vertices of the other color. The trick then is finding what R(m,n) is for a particular combination of m and n you’re interested in.
The article took me back to the days of my Number Theory class in college. I vaguely remember the term clique being brought up. In looking it up I found that there are Maximal, and Maximum cliques with a Clique number and a Complete Subgroup as part of this. Best example (I think) would be the cliques in High School where the members (football jocks, cheerleaders, nerds, mean girls..) are tightly connected to each other as a subgroup with a limited number of members which are part of the larger group i.e. High School. This sounds like something that makes “order out of chaos” something said by a Borg Queen.
What is Maya trying to do with this collection of words? Show off? Pay the rent by articles or word count? Annoy the readers?
I’m afraid to ask a friend who has multiple math degrees because she will very likely ELI5 in one or two sentences… gee…
Math gets to have its own terminology just like every other field. In this case, the concept is like this. If you have a table with a certain number of seats, you can invite anyone in the world at random but math will be able to prove something about the group of people. Any two people have either met each other or they haven’t, so that’s something this can apply to.
**If the table has six seats, then math says that there’s got to either be three people who all met before or three people who never met each other. If one isn’t true the other one has to be. **
(Imagine there were three couples. If so, either each couple never met the other couples, in which case you can take one from each couple and get three strangers, or one couple did meet somebody from another couple and you can take those three and get three acquaintances.)
But that’s only 6 seats, 3 friends, and 3 strangers. If you want different numbers with the same word problem, you have to use more exact terms like the math people do in order to describe the problem in a way that it applies to any numbers you could give it. And of course you have to change it from seats and friends to something more generic. If Maya was trying to pay by word count, she could have explained all the terms; it’s way more compact to skip explanations.
The interpretation of order seems to come from the relationship between the number of sides and the number of vertices, coupled with the rules imposed on the test. A vertex with an even number of sides can be passed through more than once, a vertex with an odd number will be singular start/end point. Because all the points are necessitated to be connected, symmetries are formed, producing a mirror or rotational pattern depending on the number of vertices being odd or even.
Perhaps it’s just psychosomatic.
Not a fan of this article. Way too little detail and too deep in a topic that not many would be familiar with.
It ends up feeling very hollow.
“Apophenia (/æpoʊˈfiːniə/) is the tendency to perceive meaningful connections between unrelated things.”
“The term (German: Apophänie from the Greek verb ἀποφαίνειν (apophaínein)) was coined by psychiatrist Klaus Conrad in his 1958 publication on the beginning stages of schizophrenia.”
https://en.wikipedia.org/wiki/Apophenia
Anyone remember Aronofsky’s “Pi”?