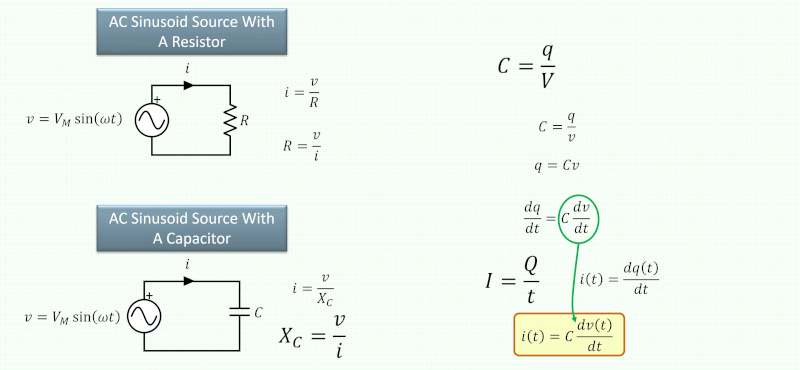
If you’ve dealt with reactance, you surely know the two equations for computing inductive and capacitive reactance. But unless you’ve really dug into it, you may only know the formula the way a school kid knows how to find the area of a circle. You have to have a bit of higher math to figure out why the equation is what it is. [Old Hack EE] wanted to figure out why the formulas are what they are, so he dug in and shared what he learned in a video you can see below.
The key to understanding this is simple. The reactance describes the voltage over the current through the element, just like resistance. The difference is that a resistance is just a single number. A reactance is a curve that gives you a different value at different frequencies. That’s because current and voltage are out of phase through a reactance, so it isn’t as easy as just dividing.
If you know calculus, the video will make a lot of sense. If you don’t know calculus, you might have a few moments of panic, but you can make it. If you think of frequency in Hertz as cycles per second, all the 2π you find in these equations convert Hz to “radian frequency” since one cycle per second is really 360 degrees of the sine wave in one second. There are 2π radians in a circle, so it makes sense.
We love developing intuition about things that seem fundamental but have a lot of depth to them that we usually ignore. If you need a refresher or a jump start on calculus, it isn’t as hard as you probably think. Engineers usually use vectors or imaginary numbers to deal with reactance, and we’ve talked about that too, if you want to learn more.















I sometimes wonder… this is high school level physics (where I went to school). It is not complex. We are not discussing quantum mechanics. What is it about the education system that people don’t know this? Surely people interested in electronics should have paid attention in class? Or don’t they teach that in other places?
Yeah, educating people is great, and should be done, in fact I enjoy doing that myself – though I prefer doing it in person.
A lot of people, including engineers, turn off their brain when they see math that is beyond “enter value for X and punch it in a calculator”
I remember some vague reasoning about the equations along the hand wavey lines of it must relate to frequency, inductance (or capacitance) and has to be inverse or not.
Good enough for me!
But I do like the video.
Just too many people learn by memorizing and get promoted just by repeating. This also happens at work – people who memorize what to do are considered better workers. True understanding helps on rare occasions.
It’s really hard to know if someone understands or just remembers.
There’s memorizing and there’s understanding, but understanding won’t happen without memorizing because you wouldn’t have anything in your head to think about.
Memorization alone doesn’t get you very far without understanding though, because trivial facts don’t account for how to apply them. The higher you go in abstraction, the more gibberish and hard to remember things become if you don’t understand them, because you need the understanding to anchor the information to something.
One of the failures of modern education is poo-pooing on the memorization part, calling it useless because you can always look it up later. Now, there’s a concept in education called the zone of proximal development, where people can perform above their level as long as they have suitable “scaffolding” to perform the task. Once the learner has learned the task, the scaffolding is removed because the required knowledge is internalized, and they can go up a level – except when it isn’t, because you’re not requiring the person to memorize anything – just to “understand” the concepts so you can look them up later when needed. But the understanding is there for as long as the person can reflect on the supplied information and references, and goes away once the person is cut off from support. Understanding doesn’t happen without memorization, remember? The ideas become very difficult and inefficient to think about.
So, you get people who can vaguely remember that there’s this thing called “algebra” or “calculus”, but when it comes to applying them, it’s too much of an effort to re-learn the mechanics and not enough time to do so, so they just give up. Turns out it would have been better to just drill them in to memory rather than “understand” the concepts using educational crutches to pass the tests at school.
I’m not sure I see what you’re saying. An average electronics hobbyist doesn’t have an EE degree. I don’t think there’s any general high school or college coursework that every person has to take and that would explain how these things work.
Most people learn from hobby books or websites, and the vast majority of them don’t derive these formulas. They’re just presented as facts.
If anything, I think the explanation in the video is more complicated than needs be. I have a simple intro here that doesn’t depend on prior knowledge of calculus: https://lcamtuf.substack.com/p/primer-core-concepts-in-electronic
Back in school I took the effort to derive things when simply memorizing them would be sufficient. It took longer at the time but I didn’t mind at all just because I found it fascinating. Time spent doing something fun doesn’t feel like work and all that. At the time it let me re-derive stuff on the fly (exams) that I forgot or didn’t/ couldn’t memorize. Now decades later I see something like this and it is perfectly intuitive even after all these years. and still just as fun. shrug.
When I was in Electronics (2 year college course) we went over the formulas…but more often than not the teacher just said “Here is the formula…the way it is derived is in the book and you probably won’t ever need to do it. If you want to learn it talk to me after class”.
Quite often there isn’t enough time to teach the more advanced math along with the theory…also in the 30 years since school I have never needed to derive it further, so I would say my instructor was correct in not wasting time on it.
As someone who just earnes an EE degree, I can definitively say that you absolutely derive these equations. Rarely are the reactance equations used directly; you must derive equations for transfer functions and current/voltage of a node/component.