“Everything should be made as simple as possible, but not simpler.”
Albert Einstein
Our journey begins with a fictitious character whom we shall call [John Doe]. He represents the average professional worker who can be found in cities and towns across the world. Most everyday, [John] wakes up to his alarm clock and drives his car to work. He takes an elevator to his office and logs on to his computer. And he does these things without the slightest clue of how any of them work. While he may be interested in learning about the inner workings of the machines and devices he uses on a daily basis, [John] does not have the time and energy to invest in doing so. To him cars, elevators, computers and alarm clocks are completely different and complicated machines with hardly any similarities. It is simply not possible to understand how each of them work without years of study.
The regular readers of Hackaday might see things a bit differently than our [John Doe]. They would know that the electric motor that moves the elevator is very similar to the alternator in his car. They would know that the PLC that controls the electric motor that moves the elevator is very similar to the computer he logs in to. They would know that on a fundamental level, the PLC, alarm clock and computer are all based on relatively simple transistor theory. What is a vast complicated mess to [John Doe] and the average person is nothing but the use of simple mechanical and electrical principles to the hacker. The complication resides in how those principles are applied. Abstracting the fundamental principles from complicated ideas allows us to simplify and understand them in a way that pays homage to Einstein’s off-the-cuff advice, quoted above.

Many of you look at The Calculus the same way [John Doe] looks at machines. You see the same vast, complicated mess that would require a great deal of time and effort to understand. But what if I told you that calculus shares a commonality in much the same way many different machines do. That there are a few basic principles that anyone can understand, and once you do, it will unlock a new way of looking at the world and how it works.
The average calculus course book is a thousand pages long. The [John Does] of the world will see a thousand difficult things to learn. The hacker, however, will see two basic principles and 998 examples of those principles. In this series of articles, I’m going to show you what these two principles – the derivative and the integral – are. Based on work done by Professor [Michael Starbird] of The University of Texas at Austin for The Teaching Company, we’ll use everyday examples that anyone can understand. The Calculus reveals a particular beauty of our world — a beauty that arises when you’re able to view it dynamically as opposed to statically. It is my hope to give you this view.
Before we get started, it pays to understand a little of the history of how The Calculus came about, and how its roots lie in the very careful analysis of change and motion.
Zeno’s Paradox
Zeno of Elea was a philosopher in the fourth century BC. He posed several subtle but profound paradoxes, two of which would eventually give rise to The Calculus. It would take over 2,000 years for man’s ingenuity to solve the paradoxes. As you can imagine, it wasn’t easy. The difficulties largely revolved around the idea of infinity. How do you deal with infinity from a mathematical perspective? Sir Isaac Newton and Gottfried Leibniz would go on to independently invent The Calculus in the mid 17th century, finally putting the paradoxes to rest. Let us take a close look at them and see what the fuss was all about.
The Arrow
 Consider the arrow flying through the air. We can say with reasonable and competent assurance that the arrow is in motion. Now consider the arrow at any given instant in time. The arrow is no longer in motion. It is at rest. But we know the arrow is in motion, how can it be at rest! This is the paradox. It might seem silly, but it’s a very challenging concept to deal with it from a mathematical point of view.
Consider the arrow flying through the air. We can say with reasonable and competent assurance that the arrow is in motion. Now consider the arrow at any given instant in time. The arrow is no longer in motion. It is at rest. But we know the arrow is in motion, how can it be at rest! This is the paradox. It might seem silly, but it’s a very challenging concept to deal with it from a mathematical point of view.
We’ll find out later that what we’re really dealing with is the concept of an instantaneous rate of change, which we will elaborate on with the idea of one of the two principles of calculus – the derivative. It will allow us to calculate the velocity of the arrow at an instant in time – a monumental feat that took over two millennia for mankind to reach.
The Dichotomy
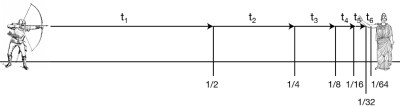 Let us consider the same arrow again. This time let’s say the arrow is coming at us. Zeno says we don’t have to move, because it can never hit us. Imagine that as the arrow is in flight, it has to cover half the distance between the bow and the target. Once it reaches the half way point, it has to do this again – move half the distance between it and the target. Imagine that we keep doing this. The arrow is constantly moving halfway between its origin and target. By doing this, the arrow can never hit us! In real life, the arrow does eventually hit the target, leaving us with the paradox.
Let us consider the same arrow again. This time let’s say the arrow is coming at us. Zeno says we don’t have to move, because it can never hit us. Imagine that as the arrow is in flight, it has to cover half the distance between the bow and the target. Once it reaches the half way point, it has to do this again – move half the distance between it and the target. Imagine that we keep doing this. The arrow is constantly moving halfway between its origin and target. By doing this, the arrow can never hit us! In real life, the arrow does eventually hit the target, leaving us with the paradox.
As with the first paradox, we’ll see how to resolve this issue with one of the two principles of calculus – the integral. The integral allows us to deal with the concept of infinity as a mathematical function. It is an extremely powerful tool to scientists and engineers.
The Two Principles of Calculus
The two main ideas of The Calculus will be demonstrated by using them to solve Zeno’s paradoxes.
- The Derivative – The derivative is a technique that will allow us to calculate the velocity of the arrow in “The Arrow” paradox. We will do this by looking at positions of the arrow through incrementally smaller amounts of time, such that the precise velocity will be known when the time between measurements is infinitely small.
- The Integral – The integral is a technique that will allow us to calculate the position of the arrow in the Dichotomy paradox. We will do this by looking at velocities of the arrow through incrementally smaller amounts of time, such that the precise position will be known when the time between measurements is infinitely small.
It’s not difficult to notice some similarity between the derivative and integral. Both values are calculated by examining the arrow with increasingly finer time intervals. We will learn later that the integral and derivative are in fact two sides of the same ceramic capacitor.
Why Should I Learn Calculus?
We are all familiar with Ohm’s Law, which relates current, voltage and resistance in a simple equation. However, let us consider “Ohm’s Law” for a capacitor. A current flow through a capacitor is dependent on the voltage across it and time. Time is the critical variable here, and must be taken into account in any dynamic event. Calculus lets us understand and measure how things change over time. In the case of a capacitor, the current through it is equal to the capacitance multiplied by volts per second, or: i = C(dv/dt) where:
- i = current (instantaneous)
- C = Capacitance in Farads
- dv = change in voltage
- dt = change in time
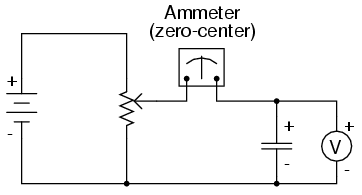 In this circuit, there is no current flow through the capacitor. The volt meter will read the battery voltage and the ammeter will read zero amps. So long as the potentiometer is not moved, the voltage on the meter will be steady. Our equation would say that i = C(0/dt) = 0 amps. But what happens when we adjust the potentiometer? Our equation says there will be a resulting current flow in the capacitor. This current flow will be dependent on the rate the voltage changes, which is tied to how fast we move the potentiometer.
In this circuit, there is no current flow through the capacitor. The volt meter will read the battery voltage and the ammeter will read zero amps. So long as the potentiometer is not moved, the voltage on the meter will be steady. Our equation would say that i = C(0/dt) = 0 amps. But what happens when we adjust the potentiometer? Our equation says there will be a resulting current flow in the capacitor. This current flow will be dependent on the rate the voltage changes, which is tied to how fast we move the potentiometer.
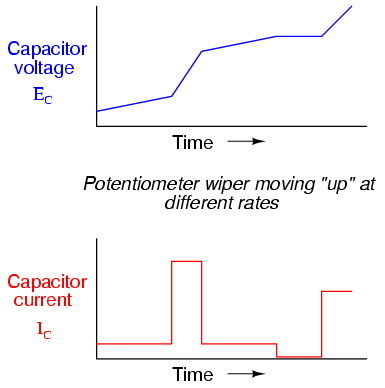
These graphs show the casual relationships between the voltage across the capacitor, the current through the capacitor and the speed we turn the potentiometer. It starts with the potentiometer turning slowly. An increase in speed results in a faster changing voltage which in turn results in a dramatic increase in current. At all points, the current through the capacitor is proportional to the rate of change of the voltage across it.
Calculus, or more specifically the derivative, gives us the ability to quantify this rate of change, so that we can know the exact value of current running through the capacitor at any given instant in time. The same way we can know the instantaneous velocity of Zeno’s arrow. It is an incredibly powerful tool to have in your hacking arsenal.
In the next article, we will go into deep detail of how we calculate the derivative using a modern but still simple representation of Zeno’s “The Arrow” paradox and some basic algebra. A following article will do the same for the integral using the Dichotomy paradox. Then we will tie things up by showing how the two are related, something known as The Fundamental Theorem of Calculus.

















I am greatly enjoying these in-depth series of informational articles. It would be very nice if there were an index page of all such series, with links to each post.
Thanks for the compliment!
Everyone here agrees with you about making these posts more persistent and easier to find after the fact. We’re working on a solution and I hope to have something awesome early in the new year. I’ve mentioned that the content in the Omnibus is too important to only be viewed during the 15 hours it’s on the front page (sometimes less) but these days that sentiment goes for a lot of our content.
Useful tags and informational headlines would be a great way to start. Then all you have to do is implement a page that lists all of the titles for each tag on a single page.
I think just having something like a learning zone on the website would help. You could put all tutorials and informative theory in this area.
“Hackaday University”?
School of hard hacks. LOL
“What is a vast complicated mess to [John Doe] and the average person is nothing but the use of simple mechanical and electrical principles to the hacker. ”
Well, it’s both, really. Simple principles applied everywhere has produced kind of a vast, complicated mess.
Over a century old and still great!
“Calculus Made Easy” by Silvanus P. Thompson (1851-1916)
http://www.amazon.com/Calculus-Made-Easy-Silvanus-Thompson/dp/0312185480/ref=sr_1_11?s=books&ie=UTF8&qid=1450205967&sr=1-11&keywords=calculus
FYI, It’s also on Project Gutenberg as a free pdf.
Wow this book is amazing! Thanks for the tip
For anyone else, the free pdf version can be found here: http://www.gutenberg.org/ebooks/33283
“Being myself a remarkably stupid fellow, I have had to unteach
myself the difficulties, and now beg to present to my fellow fools the
parts that are not hard.”
What a delightfully written text – I think I will enjoy!
@bobfeg: It’s a fantastic book and it’s free! (off-topic: I wish there was a “like” button here for comments/replies).
+1
YOur capacitor analogy is very similar to the analogy that my 3rd calculus professor gave me, that finally made calc “click” for me.
Your description of the paradox of the arrow is missing something very important. As stated here, it merely asserts that the arrow viewed at one instant is at rest. To properly present the paradox of the arrow you need to include the reason why Zeno said the arrow was at rest when considered in a single instant. Otherwise it looses much of its impact.
Also, I’m going to say that I believe that The Limit is also a very fundamental part of calculus, and is important for actually understanding both The Derivative and The Integral (and The Series), in any depth beyond basic intuition. I would also state that I believe it to be important to calculus in its own right.
THIS. Limits are a very fundamental part of calculus. In fact when I learned it, the very first thing we started with was reviewing and expanding the idea of a limit.
+1 I recall the solution the the 1/2 of 1/2 of 1/2…paradox is found by use of a limit. The limit is also the way derivatives are shown to exist and the way their values were determined – and still are when they get tricky. Integral and derivative sound OK until someone sees a big integral with the strange symbols. Newton’s fluxion nomenclature did not catch on. Perhaps because the Principia Mathematica has such difficult painstaking geometric proofs.
A foundation in geometry and limits makes Calculus a lot easier. And lets not forget how Feynman credits the algebra club in high school and contests in factoring polynomials.
I think it is important for anyone in engineering and physics to get a good grip on the words used in older literature. In the case of the Integral Calculus, Quadrature was the problem of finding area and the driving force behind Integral Calculus. It had real world application and was much more interesting than Zeno. Early mathematicians did not publish. They kept their methods secret to make a living off them. It is worth saying Integral Calculus and Differential Calculus because there are many other things called a Calculus. You even hear people today says things like “the political calculus”. It is just verbal filler but it sounds smart.
“algebra club in school”… our school didn’t have one or I would of been its only member.
“the arrow was at rest when considered in a single instant. Otherwise it looses much of its impact.”
I see what you did there… B^)
Just what I needed, and a good explanation of John’s problem, I’ve always seen Calculus as a brick wall.
I have an idea that a lot of equations of that type could be represented more easily using code, either BASIC or pseudocode. The idea of things changing is easier to imagine step by step, as in a FOR loop. If that idea’s useful, please use it.
For me at least, the brick wall was imposed by the method of delivery. Differentiation was introduced by a way of calculating the gradient of a straight line, i.e. rise over run. A little while later a whole series of derivatives was introduced what amounted to several pages of formulae. Integration was then introduced as the reverse process of differentiation, and then a little while later as a method of finding the “area under the curve”. If they were instead introduced as means of solving these paradoxes, i.e. as part of something dynamic, then it probably wouldn’t have been a brick wall, but merely a drywall.
That’s called a Runge-Kutta approximation, if I spelt it right.
We had to write a program to solve a differential equation in a college class I took in the late 80’s, using the Euler and Runge-Kutta methods. Being that I transferred to this school, and didn’t have FORTRAN behind me, I was the sole classmate to write the program in GW-BASIC. I got to learn about dimensioned arrays pretty quickly. At .001 intervals, my 10 MHz Laser Compact XT took an hour to run. I added a beep code to go off every few minutes so I knew it was still running. I still tempted to run that code on a new computer… probably spit out the answer as soon as I pressed “return”…
Heh, I was just about to dive back into fundamentals after reading this
http://www.math.harvard.edu/~knill/pedagogy/pechakucha/
(pdf http://arxiv.org/pdf/1403.5821.pdf)
http://www.matematicasvisuales.com/english/html/analysis/ftc/ftc1.html
http://acko.net/blog/to-infinity-and-beyond/
ps: the twitter sign on is a bliss.
just wait until common core get’s their hands on calculus. Then nobody will ever want to go into anything STEM.
Have you ever seen what happens to people who mess with the engineer’s stuff?
Day after day, it becomes more clear that ancient Greece was both the spark and the flame of civilization.
From medicine to engineering, from maths to philosophy.
And fabulous army uniforms.
If you need a review, check Amazon and Alibris for used paperbacks of “College Mathematics” by Kaj L. Nielsen. Everything you need without all the pretty pictures of happy school kids and marginalia. Condensed and concise.
If I may be a bit pedantic – it is probably incorrect to say “current flow through the capacitor”. Since current is the flow of charge, then it is more accurate to state “charge flow through the capacitor”, or “current through the capacitor”…
Depends on the capacitor chemistry, current certainty flows through a super capacitor. Ionic movement is current as is electrons moving.
Although current does flow through a regular capacitor as well.
https://www.youtube.com/watch?v=ppWBwZS4e7A
Right. The answer is “NO!”. It isn’t that hard and doesn’t need to be confusing. The electrics 101 equations are derived from the more fundamental behavior. The capacitor allows charge to be pushed by electric fields. Various means are used to provide plates with very large area (like rolling up foil with paper in between) or greater energy stored in the electric field (dipole molecules that get twisted out of position as the field grows). You can’t push electrons very far. The force needed is enormous. How far depends on the field strength, the volts per meter across the gap. How much depends on the area of the plates.
You have to ask in DC why does it stop flowing? Current flows to the plate on one side and is pushed out of the plate on the other side. The electric field is only so strong and and can only shove so many electrons away from equilibrium. Increase the voltage and you push a little harder. Open the switch and the process reverses (not shown in the video).
But do it in a vacuum. Charges on one plate push charge on the other due to an electric field – the electromotive force – that exists between the terminals of the power source. No charge moves through the space between the plates except by accident like a short photon or cosmic ray liberating an electron from the conductor. (Nice to not mention that AC and caps require the algebra of complex numbers and those EE101 equations are useless. As he says, that is a whole other series of videos).
Capacitors BLOCK current and store charge, or require charge to store energy. The “YES” answer is too misleading. You can’t run Kirchhoff’s laws around the circuits with caps, not in their recognizable algebraic form.
[Use an electrometer instead of a Triplet and show charge and discharge :-) ].
Capacitors most certainly allow current to flow through them. If you are saying that current does not flow through them because a given electron (ignoring quantum properties) will not move from one plate to the other, then you are adopting a much too strict interpretation of electrical current. I can push current in to one lead of a capacitor, and get the exact same current out of the other lead. The device obeys Kirchoff’s current law (the sum of currents into and out of a node is zero).
Consider a pipe with a sliding plug in it, and a pair of small ridges in the pipe confine the plug to a certain region of the pipe, and the pipe is filled with water. If I pump water into one end of the pipe at a given rate, water will flow out of the other end of the pipe at the same rate (add a spring tying the plug to a particular spot in the pipe and you essentially have a hydraulic capacitor). If I make put the ridges in the pipe arbitrarily far apart (allowing the plug to slide over an arbitrarily long length of the pipe), I might need to pump water into the pipe for an awfully long time before I realize that the plug is even present. At what point do I say “there is a sliding plug in here that prevents the water that enters one end of the pipe from ever getting to the other end of the pipe?”, or do I simply state the obvious that water clearly is flowing through the pipe? I don’t get bogged down with the semantics of what it means for water to flow through something…
When we deal with AC currents, we can (very easily) build circuits that are physically large enough that individual electrons (to the degree to which we can refer to individual electrons) will never flow completely through the circuit. Think of a loop antenna larger than a half wavelength long. A given electron will never make the full trip through the loop from one end to the other before it reverses direction and flows back towards the source. By the same argument as is given for the capacitor, I could claim that current doesn’t flow through the antenna because in practice it never does flow “all the way…” But, we’re just talking about a simple copper wire!!! If I can (and I do, correctly) say that current flows through a loop antenna, then I can say that it flows through a capacitor.
” I can push current in to one lead of a capacitor, and get the exact same current out of the other lead. The device obeys Kirchoff’s current law (the sum of currents into and out of a node is zero).” So you can describe this AC current with simple algebra and arithmetic?
Your pipe and plug analogy is strained. I think you mean you can shake the water back and forth but it never passes through the pipe and never mixes because of the plug. That is the problem with attempting analogies for things that need to be described on a complex space. We get the same over-simplifications with in-phase and quadrature detection and processing in radio, or in Fourier optics, or liquid crystals and polarizers.
” Think of a loop antenna larger than a half wavelength long. A given electron will never make the full trip through the loop from one end to the other before it reverses direction and flows back towards the source.” I’m trying but you lost me. The electrons barely move in an antenna, half wave or not. Maybe you are thinking of microwaves from Klystron tubes or cyclotrons where the electrons are going near the speed of light, not just the electric field?
I am unconvinced. Let me encourage you to adopt the notion that you can send power through a capacitor, but not current.
Current doesn’t flow through a capacitor. An effect does.
My point is that the models that we use to design with electronic and electrical components are abstractions, and without those abstractions nothing ever would get done. We talk about wires, but every wire is really a resistor in series with an inductor, with lots of capacitors connecting it to all sorts of other things in our systems. We say that electricity flows from positive to negative, when we know for a fact that this is incorrect. Every semiconductor that you can lay a finger on is vastly more complex in its precise behaviour than any of the models that we use to design with them.
For all intents and purposes, current flows through a capacitor. I don’t need complex numbers to deal with AC current through one either – only when I want to deal with currents of different frequencies, and even then only when I want to know the instantaneous current through the capacitor. Then again DC is just another frequency. I know the impedance of a capacitor, so I can tell you the current through it given excitation frequency. At DC, I know that the impedance is infinite, so I know the DC current is zero. At AC, I know that it’s finite, so I know that the AC current through it is non-zero. The fundamental equation describing a capacitor (i_c = Cdv/dt) is expressed in terms of its current.
At the base physical level, I know that electrons (if everything is working the way that it should) do not migrate from one plate to the other, but we don’t worry about accounting for individual electrons in electrical engineering. We worry about mass flow. That is why I started off my post by saying that the “no” side is taking too strict of an interpretation of current.
I agree that we get a lot done with the simple rules. But I’m not convinced that it is a good thing to use them without caveats. Like say DC when you want to use the DC equations. The video ends with a demo that is not DC. It looks like a simple charging curve. However there is resistance in the right places to properly call ti a low pass filter. Or just take the capacitor in a circuit and connect a resistor to ground on one side. If the is any AC (and there is always a little from noise). If you want to analyze the circuit response, you are suddenly launched from nice friendly DC to equations that look pretty familiar but have X instead of R and a sprinkling of ‘j’s as the square root of -1 and Omega for radial frequency and few pi’s added in for fun. There is talk of finding magnitudes using complex conjugates and phase from the ratio of real and imaginary parts. In some first year EE text books this comes on quickly. The increased complexity is all because current does NOT pass through capacitors.
The complexity is not because current does or does not pass through a capacitor. It’s because of the derivative relationship in its defining law of behaviour. Inductors pass current and have the same complexity (in some ways worse because you can much more easily get interaction with neighbouring components with inductors), just 180 degrees different in phase. An open switch does not pass current. A closed switch always does. Capacitors and inductors pass current, but based on a first order derivative relationship between voltage and current with respect to time.
Calling upon a mathematical “law” as a cause of physical behavior is, well, backwards, the laws being approximations. The complexity is not the same as inductors. Inductors can conduct current around a circuit. The equations involving energy storage look like inversions of each other because of the commonality of energy storage. But what do they reduce to at DC? Certainly quite different.
Yup, you’re right. Current’s already a flow (of charge). How about “current flowing through…”?
Current moves into and out of a capacitor, but not through.
Great article on Calculus! Looking forward to the next article that will “go into deep detail of how we calculate the derivative using a modern but still simple representation of Zeno’s “The Arrow” paradox and some basic algebra”.
Is there a math equivalent to allaboutelectronics?
I guess it’s sosmath.com
I don’t know why most of the people hate it. But out of most topics , calculus is my favourite one in combined maths syllabus. The article is great. Keep it up
Should be: “Zeno of Elea 490 – 430BC”. You write BC dates in reversed order according to their absolute value.
Fixed. THanks!
Calculus not so hard. I reinvented it when I was sixteen (without knowing I did so).
A friend worked for an asphalt contractor. He asked if asphalt is thicker in middle of road than at edges how do you figure volume? After thinking real hard about it I suggested the only way I could figure it was to divide area into small pieces based upon rate of thickness change over distance and add up area of all the pieces. (Volume also including distance down road). Found out in high school calculus that was how Integral calc worked.
Undoubtedly had you chosen to further express your vast genius it was only another afternoon on the asphalt to extend your cute little exercise into the fundamental theorem of calculus, for surely you had already mastered the profound implications of that theorem. thanks for the laugh.
Nasty case of sarcasm you got there…
Using calculus-like methods to solve a quadrature problem without training is an impressive accomplishment. If you had examined the problem until you discovered the fundamental theorem of calculus and proven your result with the limit of a converging series. ……. (I don’t know if you did or not. If you did, congrats! I’m one of those fools who had to unlearn all the Tom Swift and Doc Savage non-science. Catching onto calculus changed my world view dramatically.)
Ready for part 2!
I have high hopes for the following articles! Calculus is something I’ve attempted to grasp on several occasions, but the educational sources have not been intuitive at all (including khan academy). Even those intended for the mathematically challenged seem to assume you should already know so much, or that graphs should suitably convey the concepts of it. Personally, I’m terrible at rote learning, especially when it’s something I’m learning in my spare time and have little patience for tedium. I need to grasp the fundamental problem before I can dig into the methods and the reasoning behind it that provides the solution. I know of calculus, but I don’t know why there’s calculus or what it is that it’s useful for. We’re off to a good start here. I hope that I will understand the integral and derivative (and limits!) at last!
i think that’s an intrinsic problem of teaching. You can only teach something once you already know it (and hopefully understand it, with schoolteachers being an exception). Things make sense a certain way when you understand them, but that might not be the correct way to build the understanding from scratch. Teaching is definitely a skill in itself.
I’ve always found that I learn best from stories, and analogies. It’s something I do if I’m trying to teach a friend or relative something, usually computer-related. Actually my 70-something (I know how old she is, but it’s not polite to tell) grandmother is much better at learning than many people younger than her. Partly because she isn’t offended at the idea of having to learn something, partly because she isn’t embarassed to use her brain.
Why is it that it’s fine, and likeable, for people to say, “Oh, I’m thick, don’t ask me!”, but annoying for someone to know things? I realise there’s such a thing as being a know-all, spouting information where it isn’t wanted or appropriate. But still it really isn’t the done thing to show intelligence too often, showing ignorance is fine as often as you want. Were people always like this?
Excellent read, really enjoyed. Just couldn’t resist adding:
http://imgur.com/iuMazE9
Too many kinds of calculus, differential, integral, of variations, multi-variate, of complex variables, on vector spaces ……
So it’s “those calculus” then? Calculi? Calcules?
Contravarient covarient tensor plus too confusing with kidney stones – google staghorn calculi for one type.
You may want to check out http://www.mathics.org/ here is an excerpt from this page: Mathics is a free, general-purpose online computer algebra system featuring Mathematica-compatible syntax and functions. It is backed by highly extensible Python code, relying on SymPy for most mathematical tasks.
I’m just a user of mathics and not involved in this project but I like it because it’s open source and hackable.
It’s not as hard as you think, but teacher often suck at explaining it and the exam you have to do on it can be hard or un-intuitive for the average student.
Yeah i’m a bit bitter because decades ago, math almost wasted my life. People keep telling me “oh to learn computer programming you need to know math”. Truth is they didnt have a clue and fooled me. So instead of stating programming earlier I just waited…
When I finally learned programming it was a revelation: It was the other way around, computer would help me understand math. It helped me improve my mental calculation ability by using all sort of trick when I was programming assembly language. Mostly fixed point arithmetic, avoiding long division, using combination of addition and multiply or substraction…
Oh well…