A talk, The Unreasonable Effectiveness of the Fourier Transform, was presented by [Joshua Wise] at Teardown 2025 in June last year. Click-through for the notes or check out the video below the break for the one hour talk itself.
The talk is about Orthogonal Frequency Division Multiplexing (OFDM) which is the backbone for radio telecommunications these days. [Joshua] tries to take an intuitive view (rather than a mathematical view) of working in the frequency domain, and trying to figure out how to “get” what OFDM is (and why it’s so important). [Joshua] sent his talk in to us in the hope that it would be useful for all skill levels, both folks who are new to radio and signal processing, and folks who are well experienced in working in the frequency domain.
If you think you’ve seen “The Unreasonable Effectiveness of $TOPIC” before, that’s because hacker’s can’t help but riff on the original The Unreasonable Effectiveness of Mathematics in the Natural Sciences, wherein a scientist wonders why it is that mathematical methods work at all. They seem to, but how? Or why? Will they always continue to work? It’s a mystery.
Hidden away in the notes and at the end of his presentation, [Joshua] notes that every year he watches The Fast Fourier Transform (FFT): Most Ingenious Algorithm Ever? and every year he understands a little more.
If you’re interested in OFDM be sure to check out AI Listens To Radio.
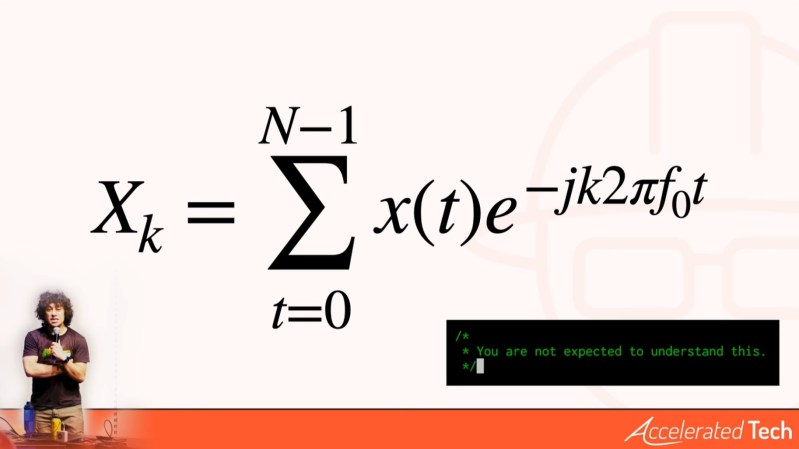
The standard notation for (discrete) Fourier Transform is mathematically compact and elegant, but it cannot be directly converted to an algorithm or analog circuit. A ALU or Opamp cannot directly calculate the square root of negative one or do non-integer or negative powers. But it can multiply a signal by a sine or cosine.
The first time I really understood Fourier transform was when I was multiplying an analog signal with a sine wave from a signal generator. I could see that if the frequency component was in the signal it would result in a DC offset. If it was in phase the DC offset was the highest magnitude(positive or negative) and if it was 90 degrees out of phase it was 0.
If you multiplied a signal with a sine and a cosine and do the average over the whole period you will get the DC offset for the sin and cos component.
Averaging is just integration and scaling.
You can do this digitally, analog electronically or analog mechanically.
Hi C, Yeah, that’s correct that it is inefficient (though, given that it is a discrete sum, you can directly convert it at least to an algorithm) — and that’s why I did not want to spend too much time on the mechanics of the Fourier Transform equation itself. As described above, for n frequencies that you wish to analyze, and m sample points, indeed, you need nm multiplications. But suffice to say indeed that the *fast Fourier transform algorithms are dramatically better, and allow you to do it in way fewer operations than that!
A vaguely different version of what you describe you discovered, for just one frequency, is Goertzel’s algorithm. Charles Lohr touched on this in his presentation at Supercon two years ago, and it was properly eyeopening for me: https://www.youtube.com/watch?v=V57f5YltIwk
All the best,
joshua
With opamps and bipolar transistors it’s possible to make log and antilog circuits, multipliers and dividers, absolute value circuits, and quadrature oscillators. From those, it’s possible to do arbitrary powers, including negative powers. Although difficult, tedious, and probably inaccurate, a Fourier transform made from opamps, BJTs, and capacitors is possible.
Of course an algorithm can be made from the standard notation for the Fourier transform, it’s not even difficult.
The Butler Matrix is effectively a massive analog fft. See https://en.wikipedia.org/wiki/Butler_matrix#:~:text=A%20Butler%20matrix%20is%20a,phase%20shifters%20at%20the%20junctions.
“With opamps and bipolar transistors it’s possible to make log and antilog circuits, multipliers and dividers, absolute value circuits, and quadrature oscillators.”
Exactly. You can make basic operators with opamp circuits. If an operator is invertible you can invert the function by putting the circuit in the feedback path of an opamp.
The equivalent of inverting a function can be done with algorithms by using Newton-Raphson method.
“Although difficult, tedious, and probably inaccurate, a Fourier transform made from opamps, BJTs, and capacitors is possible.”
I never claimed otherwise. I just wrote it cannot be made directly (naively) from the equation.
You need to rewrite the equation to basic operators:
-You cannot supply a voltage of “j” and pass it through a multiplier.
-A single DC voltage cannot be a complex number.
-Making a loop like that in hardware is hard. and requires analog memory, multiplexers/demultiplexers, and some type of clocking circuit.
But what you can do is:
– Calculate real and imaginary frequencies separately by multiplying the signal with the sine and cosine in separate circuits.
– use two voltages to represent the real and imaginary part of a frequency component. Or you can combine both components using Pythagorean formula keeping only magnitude information and discarding the phase information
-instead of a loop you do it in parallel, requires more hardware for more frequency components
Same with software. Nobody raises e to the power of j in code. They use lookup tables for sine and cosine.
For me the two biggest realizations I had were in Fourier optics and quantum mechanics. Then later in quantum mechanical formulations of optical components. Sounds smart but I am actually quite stupid
There was no dedicated Doodle for the 250th anniversary of the birth of Joseph Fourier
And in Paris there is no “Rue Fourier” in spite of the city naming a street after every other French mathematican who ever lived.
to be true to Fourier they should just try to name a street after him in regular intervals
Very interesting talk and well explained; I feel I now have at least a very basic understanding of OFDM.
This sort of mathematics always seems like witchcraft to me. It feels completely unintuitive but yet performs amazing feats of signal recovery.
That is one of the worst presentations I’ve seen, ever. Save some time and start at about 15:00 to skip all the words he uses to describe what he going to say, and start with what he actually wants to say. But it doesn’t get better.
In the spirit of adding (and not just carping), I once spent a considerable amount of time trying to find out why the Fourier transform works. Any number of references will state what it is and what it does, but almost no one will tell you why.
You can find the answer in Feynman, at section 50-4:
https://www.feynmanlectures.caltech.edu/I_50.html
Suppose you have a signal containing cos of one frequency. When you multiply by a different frequency and take the average, the average is zero. When you multiply by the same frequency, cos(a)cos(b) => cos(a+b) + cos(a-b), and since a and b are the same the 2nd term becomes cos(0) which is 1 everywhere, which integrates to infinity.
The Fourier transform multiplies the input signal by all possible frequencies simultaneously and integrates, and the result is zero everywhere except those points corresponding to frequencies in the input signal, which are infinite.
Hi Peter, sorry to hear you did not like it :) Looking forward to hearing your talk on the internals of a Fourier transform and why it works next year — I am sure I will learn a lot!
All the best,
joshua
I was on your side, then you had to hit the enter key like Dr. Strangelove. The feast…is ruined.
Don’t mind them they don’t usually have something nice to say about nice things. Thanks for putting yourself out there. Good people see ya and appreciate what you’re doing.
Explaining math is hard.
Check out the 3blue1brown channel on YouTube. It’s run by a mathematician who is really excellent at creating understandable graphics to explain heavy math concepts.
https://en.wikipedia.org/wiki/3Blue1Brown
Most of his videos are fake though. Our prof showed us during lecture and explained how he ripens the whore out of math to make something “fun” and “engaging” by putting up outright lies.
Can you point to a specific example? I have a math degree and I’ve seen many of his videos and found no issue with them beyond a bit of hand waving here and there. A lack absolute mathematical rigor in a 20 minute video is to be expected. I wouldn’t say that they are outright lies, and are instead rather valuable exercises in developing mathematical intuition.
I’m hoping there’s nothing too egregious… I’ve recommended the channel to several students and I’d hate for them to be misled!
From SteveS, above:
“Explaining math is hard.”
Wrong.
Explaining math is, most definitely, not hard if one knows what he or she is doing. People who want to explain it to you are everywhere, but finding a good math explainer is not easy…as evidenced by this ‘talk’.
If you really want to see how easy good math explainers can make any aspect of the subject, start here—
Innumeracy, John Allen Paulos
ISBN 0-679-72601-2
Mathematics–A Human Endeavor
Harold R. Jacobs ISBN 0-7167-0439-0
Who Is Fourier? A Mathematical Adventure
Transnational College of LEX; translated by Alan Gleason
ISBN 0-9643504-0-8
Calculus Made Easy
Silvanus P. Thompson and Martin Gardner
ISBN 0-312-18548-0
[The original, written by Thompson, was fist published in 1910 and has never been out of print]
“It is difficult to get a man to understand something when his salary depends on his not understanding it.”—Upton Sinclair
(…could be modified for a particular situation, e.g.,, “It is difficult to get a man to explain something satisfactorily when…” )
I’d say explaining is always hard, because you have to know why your explainee doesn’t understand in the first place. Looking at my explaining experience I can say that I’m a pretty bad explainer, because I either don’t understand myself (and therefore can’t explain), or I understand, but had trouble understanding at bits which were absolutely obvious for everyone else, so when I try to explain, I tend to state the obvious and skip what should get a closer look :(
This is a great framing.
One thing I’ve found in applied work is that Fourier’s “unreasonable effectiveness” is precisely because it collapses structure so cleanly into global frequency energy but that same strength makes it blind to certain kinds of local organization and transition behavior.
I’ve been exploring ways to build diagnostics around Fourier outputs that focus on how structure moves and redistributes rather than just where energy concentrates. Not a replacement more like a complementary lens for non-stationary or regime-shifting signals.
Curious if you’ve seen similar needs show up in practice, especially in real-world RF or sensor systems.
That’s definitely an interest. Have you ever looked into wavelets? Not the same thing but, absolutely the same arena
The Fourier transform along with the DFT and FFT must rate as my favourite ‘slice’ of maths ever. Easy to write down but not so easily understood in how it actually works. YouTube has some good and some not so good videos on the subject. Personally I found 3B1B graphically heavy but not that intuitive. Nonetheless a delicious piece of complex 😉 mathematics.
I worked for 6 years for the SETI Institute of Mountain View. In that job, they were heavily using custom FFT boards and systems to break down a 20Mhz wide spectrum of RF into .7Hz wide bins. They were looking for intelligent signatures in RF signals coming from star systems. The beauty of FFT was that you could sift through oceans of noise, and recover a coherent signal buried by hundreds of Db of noise, and clearly resolve it. Yes, it was an interesting experience. We could see the signal leaking out of Voyager 1 transmitter when the transmitter was turned off 14 Billion miles away. The signal was leaking out of a 6 inch piece of coax cable. Amazing!
As a well educated electrical engineer, I still found this talk interesting. The crux of why this all works is the exact same reason why you can make Fourier transforms more efficient. It’s a matter of projecting your signal onto its components. Each time you do that, you reduce the dimensionality of what remains to process. Hence anytime you have an orthogonal decomposition, the “divide and conquer” nature of n*logn is present by construction. In more fancy/flowery language: any unitary operator can be decomposed using butterfly schematics into tensor products of smaller unitary operators.
Thank you for indulging me temporarily. I find this talk was a wonderful reset on my perspective.
FDM has been used for a long time before now. Analog telephone signals were multiplexed in frequency since the beginning of time.
Your AM/FM radio does the same thing.
The orthogonality of sin waves of different frequencies is the key. Which is why you have to look at the FT as sliding an infinitely narrow band pass filter past a signal and summing the result of all those measurements.
Or you can look at it as computing the sum of an infinite number of dot products.