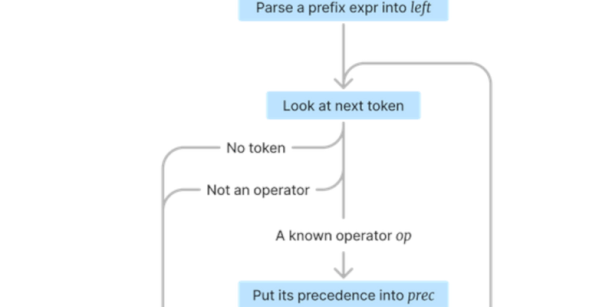
Parsing algebraic expressions is always a pain. If you need to compute, say, 2+4*2, the answer should be the same as (2 + (4 *2)), not ((2 + 4) * 2) — in other words, the right answer is 10, not 12. The classic way to do this is to use two stacks and a table of precedences for the operators. However, [Martin Janiczek] prefers to use Pratt Parsers and wants to show you how they work.
The parser is named after [Vaughn Pratt]. The algorithm works with a table of precedence where operators with higher precedence have higher numbers. It then builds a left and right portion of a string, using recursion. So if you consider 2+4*2, you wind up, on the first pass, with (2+ parse(4*2)). The second parse returns a full expression to produce: (2+(4*2)).