Parsing algebraic expressions is always a pain. If you need to compute, say, 2+4*2, the answer should be the same as (2 + (4 *2)), not ((2 + 4) * 2) — in other words, the right answer is 10, not 12. The classic way to do this is to use two stacks and a table of precedences for the operators. However, [Martin Janiczek] prefers to use Pratt Parsers and wants to show you how they work.
The parser is named after [Vaughn Pratt]. The algorithm works with a table of precedence where operators with higher precedence have higher numbers. It then builds a left and right portion of a string, using recursion. So if you consider 2+4*2, you wind up, on the first pass, with (2+ parse(4*2)). The second parse returns a full expression to produce: (2+(4*2)).
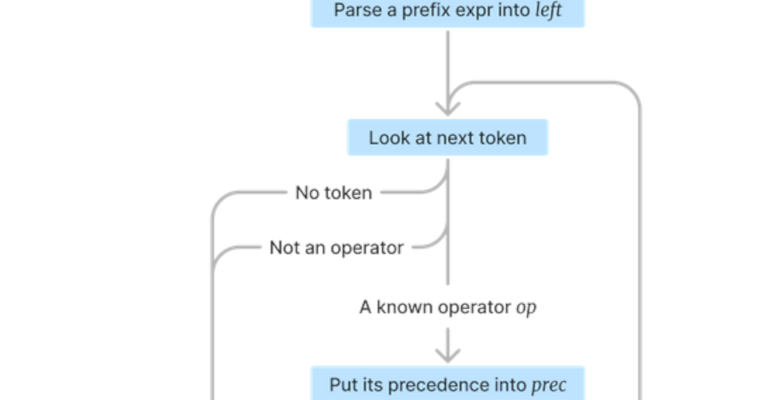
If that was too fast, read the post which has a nice flowchart and an example step-by-step parse of 1+2-3*4+5/6^7-8*9. Towards the bottom, there’s a nice animated flow chart that you can step through, almost like a debugger.
There are a few details left for the end. For example, there is a way to allow right-associative operators (e.g., 2^3^4 is actually ((2^(3^4)). You can also make some easy modifications to get things like unary negation and parenthesis.
Of course, there are other ways to go. You could stick with RPN. Or use the traditional method.















Even simpler to understand is to make a set of different functions, each responsible for different level. So you start with ‘parse_expr()’ which calls ‘parse_term()’, which calls ‘parse_factor()’. The parse_term() function will only accept expressions with ‘*’ and ‘/’ operators, but will return its result when it sees a ‘+’ or ‘-‘. For every precedence level you have a new function.
That’s the way the unix tools book does it with lex and yacc. Pretty classic.
This is called a “recursive descent” parser.
It certainly is a type of recursive descent, although the fact that it splits out differently based on operator priority is the key difference. Earlier this week we looked at a different parsing method that is also a type of recursive descent technique but also had some nuances compared to what you normally see.
How does one do the ternary operator?
The precedence function can have multiple following elements, just like a recursive descent parser. It can do the ternary operator and the if-then-else structure.
Robert Nystrom uses Pratt parsing in the second half of Crafting Compilers, which is available for free online:
https://craftinginterpreters.com/
Pratt’s original paper is pretty readable, if you want to go to the source:
https://web.archive.org/web/20151223215421/http://hall.org.ua/halls/wizzard/pdf/Vaughan.Pratt.TDOP.pdf
There is no immutable universal law that says 2+4*2 should be parsed as 2+(4*2). That’s an Earth-centric bias. I have it on good authority that on Omicron Persei 8, the expression parses as (2+4)*2.
True, but — as everyone knows — on Omicron Persei 8 the + sign indicates an inverse power and * is similar to our log function so the actual translation into Earth-speak is 2^1/log2(4). An amazing example of Hodgkin’s Law of Parallel Planetary Development (https://memory-alpha.fandom.com/wiki/Hodgkin%27s_Law_of_Parallel_Planetary_Development) that they use Arabic numerals, too!
who cares? this is just a way to convert an implicit infix expression to a more explicit expression that is still infix
evaluation is still done shunting yard style with prefix or post fix.
I just don’t see anything special here
It is trivial to handle priorities. Now do associativity.
With Pratt it’s significantly easier than with a more ad hoc recursive descent.