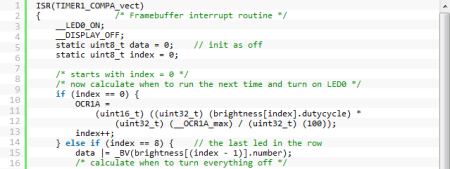
For some projects, it’s okay to have a microcontroller twiddling it’s thumbs most of the time. When a project requires the cpu to do just one thing over and over, there’s no loss with inefficient code – it either works or it doesn’t. However, if a project requires a microcontroller to do several things at once, like reading sensors, dimming LEDs, and writing serial data out, cpu utilization can become an issue. [Robert] wasn’t happy with the code he used to control a string of LEDs, so he rewrote his code. With the old implementation, [Robert]’s code used 60% of the cpu time. With the new and improved code, the cpu was only busy 8% of the time.
The code works by using a hardware timer to trigger an interrupt. After calculating the next time it should run again, and changing the state of the data line, the code just sits quietly until it’s needed again.
It’s not a pretty hack, or even one you can hold in your hands, but [Robert]’s determination in getting a μC to do what he wants is admirable.















Beautiful, I was looking at this exact problem, but with a PIC16f628A.
@doubleup I believe microchip have app notes on this, so check it up
Another good (better?) write-up for people wanting to learn how to use interrupts efficiently:
http://www.uchobby.com/index.php/2007/11/24/arduino-interrupts/
And it’s geared for Arduino users with notes on what timers to use and what will stop working when you use those timers.
Also, it covers another important aspect of using ISRs like this; namely correcting for the length of time the ISR took to run.
Thanks for that link Bill.
Using ISRs vastly improves software PWM performance. It gets a little bit trickier when trying to do multiple channels (e.g. RGB).
It’s worth noting that some chips can do PWM for you internally. Set up a few registers and you’re good to go.
Slow news day?
“Some guy used an interrupt service routine in his project, it really saved processor cycles”.
it’s a little different than your standard PWM ISR where you call the ISR on every possible PWM edge. In this case, the correct edge is calculated and instead of wasting 256 ISR calls on each PWM cycle, you only use two.
To be honest, I didn’t go through his code, but I just so happened to be writing one of these guys for the PIC16F series on Timer0 as a general purpose PWM library. Saves TONS of CPU time.
@alan – welcome to hackaday! you must be new here, and unaware that the term “hack” means “anything I didn’t learn from the Arduino Blinking LED tutorial.”
I read an article the other day on how to multitask with a microcontroller. You are basically writing your own processor scheduler to do so, but you really get to know all the inner workings of the uC.
Why on Earth would you wait 256 ISR calls to toggle a PWM pin? That’s clinical insanity. Calculating when edges occur and toggling only at those times is a technique at least as old as the Commodore 64, as I distinctly remember this technique being used to emulate RS-232 at a fairly fast rate (2400bps? I forget, precisely) using the 64’s user port, documented in a Commodore magazine article.
How this is HAD worthy by itself is beyond me, but anyway.
It could even be quite a bit more efficient to take the multiply and especially the devide operations out of the loop, and storing the timer values directly in the array.
I’ve done it countless times that way, to control LEDs, hobby servo’s, etc. Simply build an array with X masks for the outputs and X intervals. At each interrupt, simply copy apply the mask to the outputs, write the new interval in the timer (correct for length of ISR), increment the index, wrap if the end of the array is reached.
The critical observation is that, most of the time, the PWM values are updated at a rate far below the PWM frequency, so it pays to do as much as possible when updating the values, instead of every PWM cycle.
If you can understand german, this should be the end all, be all of software pwm implementations:
http://www.mikrocontroller.net/articles/Soft-PWM#Intelligenter_L.C3.B6sungsansatz
Wow this is a pretty neat haINTERRUPTED!FTW!FTW!ck.
I have split tasks two ways, interrupts, and slicing:
Tasks: http://www.mculabs.com/snippets/ptask.html
Slices: http://www.mculabs.com/snippets/slice.html
Great work! =)
@NsN: U were faster, wanted to send in the same reference! ;)
Im working with the Intelligent PWM code to dim 16 LEDs with 12bit PWM @ 60Hz on a ATMega8 while doing colour calculations and serial communication to daisy-chain up to 10 of them (at the moment)
I wonder how he measured the used CPU-time
@nippey – just use MBI5030 or similar chips. They are a little cheaper than atmega and can drive LEDs directly.
CPU time is usually calculated from instruction cycles and clock frequency. CPU datasheets should give the number of cycles required for each operation; add up the number of cycles in a routine and multiply by the clock interval (i.e. 1/freq).
@yetihehe: Already switched to a TexasInstruments 24ch 12bit PWM LED driver.
But for applications which do not exceed 16 LEDs, doing it on an atmega saves you some parts as some programmable intelligence is always needed ;)
Doing all these calculations with an AtTiny that has no single-cycle multiply is certainly far more time-consuming than 256 ISR.
Also if you drive RGB leds, with 4 bits for each color, you only handle 16 ISR and have 12 bits colors i.e. 4096 colors, most of the time far enough.
So now we compare 16 ISR with maannnyyy calculations…I keep my 16 ISR method
You gotta be kidding me. This is not a hack. This is simply how you’re supposed to program micros. Micros have these features for a reason.
I think in this world of Arduinos it has been commonplace to use terrible software looping delays. If anything, software delays are a hack not this.
Anyway regarding the actual concept of doing a lot of thing at once with a micro, the tricky thing is with crappy MSP chips (eg valueline) you have a limited number of timers. So if you have a lot of things to time, you don’t want to be squadering your precious timer if you don’t need to. If you’re really desperate you might have to resort using the wachdog timer if youve used everything up.
@Nippey: you really should use a higher PWM frequency; 60Hz looks good when you’re looking directly at the LEDs, but when your eyes are moving you can see the individual pulses. Driving behind a car with LED rear lights with a low PWM frequency gives me headaches, because your eyes are moving around all the time.
I don’t think 12 bit PWM is really useful, our eyes can’t see that many shades anyway. The disadvantage of, say, 8 bit PWM is that the difference between the low steps is pretty big, and clearly visible. A solution can be to make the pulsewidth non-lineair, but that’s somewhat complicated. Another solution can be to use dithering to be able to increase the PWM frequency without losing resolution. Thus, successive PWM cycles use a width of 2-2-3-2-2-3 etc. cycles, for example, to get an average width of 2.3 cycles, thus increasing the appearant resolution.
so this “great learning platform” make you exited in reinventing the wheel. now guess how much else you missing out
If you are going to use PWM and don’t want to take up uC cycles with it, I would suggest a uC with a built in PWM controller. The PIC 18F4431 has FOUR pwm channels, as well as several other features. All you need to do is write to a few registers to set the thing up, and then it runs. It only needs attention when you want to change the duty cycle.
My friend is working on a 12 servo driver board. He has implemented it using a 16-bit pic using the peripheral pin select function to move the output compare pin around. I don’t know if he has calculated the CPU usage but for ballpark figures he has an interrupt that fires every 2ms and in the interrupt he just changes a few register values.
You can count cycles to tell how long code is. Microchip MPLAB provides a nice stopwatch in simulate mode so that you can jump to the beginning of a routine and then run to the end and let the computer tell you how many cycles have elapsed.
If you don’t have a simulator that counts cycles for you and you still don’t want to count them manually, just use an extra I/O pin and a logic analyzer (or Oscilloscope if you have a nice digital one). Drive the line high before the timed routine and drive it low afterwards. This easily allows you to track a bunch of different events, limited only by your spare I/O and the size of your logic analizer. I don’t know how long the Arduino library takes to set / clear a pin but it should be able to be done very quickly by doing raw register writes.
@ Chris
quite any AVR has 4 PWM through OCR registers. Who cares your fat PIC18 has PWM? If it’s not to do some ad, what’s the goal of your comment?
same thing for Dr bob bob
Did you ever try AVR studio before talking? What you describe (cycle counting) if of course available through any serious simulator and hopefully on AVR Studio.
Servo driving is quite ideal for “next-time PWM calculation” as the pulse is below 2 or 2.5ms and repeated every 20 ms. In the worst case, and with a simple method, you can drive 8 servomotors through a single OCR register and much more with clever multiplexing
@ftorama: What’s up with the hostility?
@ftorama
That was un-called for. The guy made a suggestion to use a uC with hardware PWM, and gave an example PIC part that has the aforementioned capability; maybe he hasn’t had exposure to other micros (or is just better versed with Microchip parts).
More importantly, he didn’t try to shove it down your throat or claim superiority over Atmel/AVR, like you’ve made it seem.
Take your PIC vs AVR bullshit and fuck off.
@Farkanoid
Thanks for the suggestion, but I think I’ll refuse…
With the AVR (which is the heart of the article), if we need 4 PWM, we simply write some registers also…
So why anyone would need to take a 40-pin chip (you see I didn’t say PIC) for such a simple task?
@Munch: my microcontroller classes only covered the inefficient method. Today is the first time I’ve ever seen the idea of calculating the next time your ISR should run and only triggering it when you need an edge, instead of running it 256 times per PWM cycle.
It doesn’t make any sense to use interruptions to produce PWM, when the average AVR has PWM by hardware, just set it up and forget. Even the AtTiny13 has two PWM that can run at clock speed. I understand the learning curve for academic dominance over microcontrollers, like do multiplication using add and shift instead of the embedded “mul” instruction, but the academic training must be very clear, if not, several novices may think this is the only way to produce PWM in an AVR.
@SparkyGSX: Using the 16ch method on a AVR it was not possible to exceed the 60Hz, but as I already said before, I dont do this anymore.
You can get very nice chips from TI for example. Those have about ~5kHz. Maybe 10bit are enough, but who cares if get so nice low-price ICs! ;)
And talking about 8bit vs 12bit: 8bit is crap in low brightness, thats the reason for 12. And thats the reason for the calculations needed, too:
Im converting from linear RGB to non-linear ‘Eye-vision’ by a LUT and that looks very nice then.
@ftorama
The same reason some people use an entire arduino devboard to flash a single LED perhaps? Again, there are PLENTY of chips in both classes (AVR and PIC) to do hardware PWM across one or more channels in under 14 pins; Chris just gave an example chip that he’s probably worked with before.
Also, just for the sake of brevity – you did actually say PIC :P
@Volfram:
I do assume they taught you about timers and ISRs though. The leap isn’t a large one, and with a proper comp sci education, one you should have made yourself, should your situation have required it.
If you are running into a shortage of timer hardware most of your tasks usually aren’t extremely time critical. These tasks can be handled in several ways just using a periodic tick timer and some simple code. Save the majority of the timer hardware for when you really need tight timing (or hardware PWM).
Anyone wanting a thorough example of how to do this on an AVR can look at my code in CYZ_RGB. The code contains an approach for doing 16 bit pwm on 3 channels using two 8 bit counters. One drawback of using such an approach is that if you need very small duty cycles you have to keep the code in the ISRs very very simple. This is difficult to do if you want to have interrupts doing other things (clock, serial, etc.)
For LED lighting control the easy solution is to use inverse PWM. Because the perceived brightness is logarithmic .. ie in the scale 0..65535 there is a very visible difference between brightness levels 1 and 10, but essentially no visible difference between 65525 and 65535. So using inverse PWM you get to use long duty cycles for dim lights (where you can get the accuracy you need) and short duty cycles for bright lights (where the accuracy of the timing is less important)