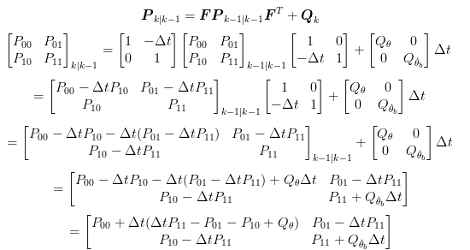
If you’re looking to improve the stability of your self balancing robot you might use a simple horrifying equation like this one. It’s part of the journey [Lauszus] took when developing a sensor filtering algorithm for his balancing robot. He’s not breaking ground on new mathematical ideas, but trying to make it a bit easier for the next guy to use a Kalman filter. It’s one method of suppressing noise and averaging data from the sensors commonly used in robotic applications.
His robot uses a gyroscope and accelerometer to keep itself upright on just two wheels. The combination of these sensors presents an interesting problem in that accelerometer input is most accurate when sampled over longer periods, and a gyroscope is the opposite. This filter takes those quirks into account, while also factoring out sensor noise. Despite the daunting diagram above, [Lauszus] did a pretty go job of breaking down the larger function and showing us where to get the data and how to use it in microcontroller code.















Did a “pretty go[od] job”?
A pretty good job?!
What are you guys on? This is an awesome piece work. Give the guy credit, I’d be willing to bet the authors of this blog couldn’t even begin to write as an informative an article.
I agree with Eccentric Electron. This writeup is not merely “a pretty good job”, it is amazingly clear, informative, and well-written.
Do not underestimate how hard it is to explain something this complex to someone not already well versed in the subject.
Lauszus’ work should be an inspiration to others, as well as an example of what a properly written treatise should be like.
In fact, I’ll put my money where my mouth is and will submit this week a simple treatise on using Euler angles to determine position of rigid bodies; specifically as it applies to robotic arms.
Here is my not-as-simple-as-I-remember treatise on coordinate transforms.
The report and appendix are in .PDF format, and the appendix also contains native Mathematica .nb code.
http://www.filedropper.com/coordinatetransforms
-Eric
Give the author credit: he did a pretty good job at underemphasizing the work done here.
In all seriousness, it is extraordinary that this work is being done and published freely and applied to applications simpler than spaceships and the like. Thank you to all that publish work like this that makes it easier for those that follow your experiences.
Hear, hear Erik!
Worth noting to those unfamiliar with Kalman Filters; each different hardware design requires its own Kalman Filter, no copying & pasting here :(
i.e. have a RC car robot, as does your friend from a different brand? each will require its own unique Kalman Filter. No real easy way around that. (or, is there…?)
And don’t forget to mention that obtaining a proper model of your system to work with is by far the hardest part of all.
Some people say that when you try to solve a problem with a Kalman filter then you have two problems. ;)
Err Kalman filters are pretty easy to do actually. The equation is a LOT nastier to look at than the raw code. as for writing another filter for each kind of hardware…no. Just tweak a few parameters and off you go. It’s just a loop and some basic math. I have no idea how to map it to that equation, but I know how to make one that works :P
http://www.scipy.org/Cookbook/KalmanFiltering
(try google cache if it won’t come up, didn’t come up for moi)
If you really think those equations are ‘horrifying’, then I’m afraid all have to hand in your geek badge.
Is not E=mc^2 the horrifying equation but the details of the undelying theory leading to it. Not saying that understanding it would be needed to just “use” it though.
In my particular case the Kalman filter was the end result of +60 college hours of one of the two quarters of discrete control theory. ;)
Or rather ‘your’ geek badge !
It seems like in this case, the P matrix, S, K[0], and K[1] will all converge to steady-state values independently of the states and measurements. (i.e. You could calculate all the P and K values before you even turn the system on.) After some number of cycles, I think you get a complementary filter and a simple bias estimator. Agree/disagree?
Not just for toys, many aircraft navigation and autopilot systems use a Kalman filter to combine inertial (gyro, accelerometer), GPS, and radio navigation signals into one extremely accurate system. I worked on such a system on the the H-53 helicopter.
It’s worth noting that a complementary filter is much simpler to program (and understand), requires much less processing power, is easier to tune, and is usually almost as good as a Kalman filter.
One of the best documents I’ve read on Kalman was written back when the filter was still new:
“Poor Man’s Explanation of Kalman Filtering, or How I Stopped Worrying and Learned to Love Matrix Inversion”
http://digi.physic.ut.ee/mw/images/d/d5/Poormankalman.pdf
There is no way I’m reading that.
Looks like it was faxed back and forth a few times…
Kudos to him for figuring out how to implement a Kalman filter. However – he chose the wrong one! No one… and I mean NO ONE uses the vanilla Kalman filter unless your problem is linear (which this isn’t). He’d get WAY better performance form using an EKF. I implemented a 3 state, 2 measurement EKF on an Arduino Uno just to benchmark what kind of update rate I could get (floating point). I don’t recall exactly but want to say it was on the order of 100-150 Hz which was plenty fast for my task.
“No one uses the vanilla Kalman filter unless your problem is linear”
What? Not really: a “vanilla” kalman filter is perfectly fine for a nonlinear system, as long as you can linearize its model around a certain point of operation, AND always keep it around that point using your control loop (which is exactly what happens here – the whole point of this bot is to stay around a vertical angle).
Sure, the linearization is acceptable only as long as your bot stays close to the vertical position, but then again, if it doesn’t, then the accuracy of angle estimation is the least of your concerns – and going back to your control loop becomes the real problem.
This requires to be well versed in mathematics/statistics indeed. I got lost at …just equal to the variance of the measurement, since the covariance of the same variable is equal to the variance.