Amateur radio is the only hobby that offers its licensed operators the chance to legally design, build, and operate high power radio transceivers connected to unlimited antenna arrays for the purpose of communicating anywhere in the world. The most complicated part of this communication system is the single-sideband (SSB) high frequency (HF) transceiver. In reality, due to the proliferation of low-cost amateur equipment, there only exists a very small group of die-hards who actually design, build from scratch, and operate their own SSB transceivers. I am one of those die-hards, and in this post I will show you how to get started.
Radio Architectures
To understand how an SSB transceiver works we must first review the basic architectures of radio receivers. My favorite way of abstracting radio architecture is to consider everything at the block diagram level: filters, amplifiers, multipliers (or mixers as we call them), and assume all blocks are impedance matched.
The earliest radio architecture was known as tuned radio frequency (TRF), which became widely adopted in the mid to late 1920s for use in consumer receivers. The signal chain consisted of an antenna to collect the radio signal which was fed into four stages of filtering interspersed with three stages of amplification. The output of the last tunable filter was fed into an envelope detector (a diode) where the demodulated audio was amplified and played out of a loudspeaker. To tune in a station you would simply tune each of the filters to the desired frequency. Later models mechanically coupled the variable capacitors of each filter section together so that the user would only need to turn one knob to tune in a station.
The problem with TRF architectures was that multiple stages of tuned filters were expensive. To address this problem Edwin Armstrong combined the use of a low-cost un-tuned filter and frequency multiplication to create what was known as the superheterodyne architecture.
Edwin Armstrong realized the value of frequency multiplication. When two sinusoidal waveforms, one at frf and the second at flo, were multiplied together the result was the sum and difference of these two frequencies, F_if = F_rf – F_lo and F_if = F_rf + F_lo.
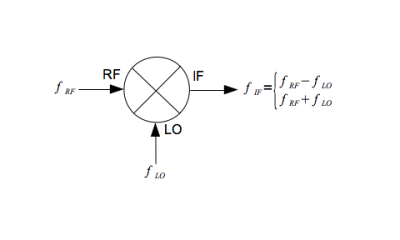
In RF design, we refer to multipliers as frequency mixers. In a superheterodyne receiver the desired RF signal is multiplied down to an intermediate frequency (IF) by use of a mixer and a variable frequency oscillator (VFO or Local Oscillator) where there exists a multi-stage filter to select the signal to pass onto an envelope detector. In other words, one of the two products from the mixer must equal the center frequency of the IF filter. To change the frequency at which the radio is receiving all you have to do is change the frequency of the VFO.
The figure below shows a block diagram of a table-top AM radio from the late 40’s where the radio tunes in stations at the frequency frf = frequency of OSC1 – 455 kHz. Changing the frequency of OSC1 changes the frequency at which the radio is tuned to frf.
SSB Receivers
Rather than demodulating the radio signal with an envelope detector a SSB receiver down-converts the IF one more time using a second frequency mixer to the audio frequency range (this second mixer is sometimes known as the product detector). The result is amplified and fed out of a loud speaker.
What is being heard on an SSB receiver is actually the radio frequency spectrum multiplied down to the audio frequency spectrum so we can listen to it. You are listening to the actual radio waves.
In this case the IF filter’s bandwidth is between 1.8 and 2.5 kHz, matched to the bandwidth of human speech. The IF filter’s center frequency and the 2nd local oscillator determine what side band is selected, either upper sideband (USB) or lower sideband (LSB). USB and LSB refers to shifting the human voice to just above and below the carrier frequency respectively.
SSB Transmitters
An SSB transmitter is simply the SSB receiver in reverse. Filters and modern double-balanced frequency mixers work in both directions. Amplifiers are wired in such a way to relays or PiN didoes so they can be reversed in transmit mode. When you transmit SSB your voice is upconverted to the radio frequency spectrum, amplified, and radiated out of the antenna.
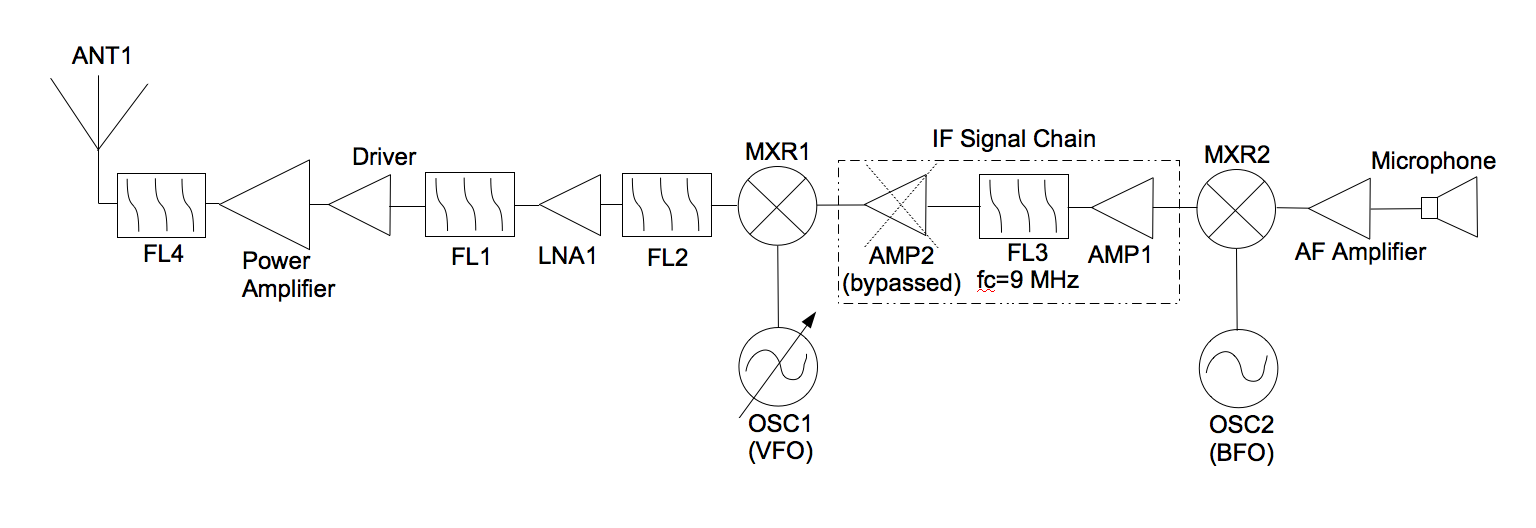
20m SSB Transceiver
The first SSB transceiver I developed was for 20m, which is arguably the most fun HF band. The marine net is on 14.300. Lots of DX during the daytime hours. From the shoreline in Connecticut I can routinely work Western Europe and deep into Russia with only 40 watts and a half-wave dipole antenna.
The block diagram of this transceiver is exactly as shown above. A lot of detail, schematics and additional info can be found here. This radio is representative of the vast majority of SSB transceiver architectures.
Next Steps
I have abstracted radio circuitry to the block diagram level. Once blocks are understood then a design can be made at the high level. After the block diagram is in place then circuits, ICs, or modules can be selected to fill in the blocks. Some circuits are borrowed from books or scaled from a design in a book. A great source for 50 ohm ICs and modules is mini-circuits. Others require the synthesis of a custom ladder network, which will be the case for the RF front-end filters. These are great resources for finding, borrowing, or synthesizing those circuits or entire radio architectures even:
ARRL handbook
Solid State Design for the Radio Amateur
Joseph J. Carr’s secrets of RF Circuit Design
Chris Boweick RF Circuit Design
Rohde’s Communications Receivers
QST magazine
QEX magazine
Build It:
There is so much more to basic RF design and the only way to really learn is to start doing it. Borrow as many circuits as you can from others. Cobble together your radio. You will get better at every aspect of design after each radio you build. Jump right in! There’s nothing like the satisfaction of making a long distance contact on a transceiver you built yourself. I look forward to communicating with some of you on the air soon!
Acknowledgement
My cousin, Juliet Hurley, MBA, MSF, MAC for type editing this post.
Author Bio
Gregory L. Charvat only operates radio equipment he builds from scratch, is the author of Small and Short-Range Radar Systems, co-founder of Hyperfine Research Inc., Butterfly Network Inc. (both of which are 4catalyzer companies), visiting research scientist at Camera Culture Group Massachusetts Institute of Technology Media Lab, editor of the Gregory L. Charvat Series on Practical Approaches to Electrical Engineering, and guest commentator on CNN, CBS, Sky News, and others. He was a technical staff member at MIT Lincoln Laboratory where his work on through-wall radar won best paper at the 2010 MSS Tri-Services Radar Symposium and is an MIT Office of the Provost 2011 research highlight. He has taught short radar courses at MIT where his Build a Small Radar course was the top-ranked MIT professional education course in 2011 and has become widely adopted by other universities, laboratories, and private organizations. Starting at an Early Age, Greg developed numerous radar systems, rail SAR imaging sensors, phased-array radar systems; holds several patents; and has developed many other sensors and radio and audio equipment. He has authored numerous publications and has received press for his work. Greg earned a Ph.D in electrical engineering in 2007, an MSEE in 2003, and a BSEE in 2002 from Michigan State University, and is a senior member of the IEEE where he serves on the steering committee for the 2010, 2013, and 2016 IEEE International Symposium on Phased Array Systems and Technology and chaired the IEEE AP-S Boston Chapter from 2010-2011
































I got into Amateur Radio because of my interest in electronics. Then I found that the vast majority of Hams are “appliance” operators. How many of them have ever even built a dipole antenna? I still look for construction articles, but about all I ever find is QRP CW projects.
Yes, that’s what i found too.
Ham radio is a hobby with almost infinite diversity. Some of us (like yourself) are into electronics and making our own equipment. Some of us just want to pick up an HT and talk to our friends. The nice thing about our hobby is that there is room enough for people from both camps, along with dozens of other types of hams as well.
There is no “right way” to be a ham, beyond the obvious one of operating legally. Stop worrying about what other hams are doing and just enjoy the most interesting hobby in the world (I might be biased).
DB — you are absolutely right. I guess I fall in the catagory of “appliance operator” — I don’t build much beyond really simple qrp TX designs, and the vast majority of my equipment are commercial-built. My hands are getting kinda shaky, and my eyes aren’t quite as good as they used to be, so building precision electronics is out for me.
However, I really like building antenna by hand, and my favorite activities involve computer generated/decoded communication, propagation studies, and (these days) qrss. In fact, a lot of what I do doesn’t even require a license; I don’t talk all that often, and when I do I don’t call CQ as the stuff I work on is pretty much scheduled via email or phone.
lol ‘biased’
I dislike ICs and searching google, would anybody happen to have a schematic for a analog tranciver in the range of 1MHz – 1GHz. It would help me learn all I need to know. Or can someone simply tell me how to transmit and receive any frequency i want, preferably without using a hundred crystals. From what I understand I can get away with using inductors and variable capacitors. would I need at least one crystal for reference? and how would that work. can you write me a book? lol thanks
The kind of transmitter you describe exists for quite a long time now (formerly known as “arc converter) : it’s a spark plug. It’s fully analogic and covers from 100kHz to 2GHz at least, particularly if you suppress the filtering cap, and will be found in any garage.
For receiving, a simple chinese USB “rtl- SDR” with an upconverter would do the job
The other way is to learn. It takes time and efforts. But if you dislike ICs and seaching google, it’s hopeless
Marc f6itu
I once read a text from a fellow radio amateur: “Hamradio”s license is a license to study…”
So many things to learn!
Well QRP is very challanging, wheathre CW or SSB. The easiest tranceiver is the CW as there are not a lot of parts. Even a simple cw transmitter could be built using a 7404 circuit.
There are very simple trancievers like the PIXIE, from the 4corners group. There are several KITS out there that have SSB and CW. Also the ham comunity is more than willing to help.
I would like to suggest looking at KQ7O’s web site if he is still on the air. Also NJQRP club.
What a thrill to make my first CW contact. It was on 40 meters. When you call CQ you don’t know who will answer.
I liken it to fishing in the ocean. When you cast out your bait you don’t know what you may catch, shark, blue fish or nothing. This Ham was in Tucson about 7 miles from I was living.
I have worked to Reading Calf on a 1 watt transceiver CW from a vertical on my roof.
What ever you deceide to do Best of Luck, Get your license the test is not difficult if you don’t have one.
Let me agree 1000% The more you play the better you get and the real fun is what you make it. A novest (beginner in radio) 1960, still play radio to day N0FCK Mack,CO
report comment
:-) because you probably don’t look in the right direction :-) have a look at the last Hackaday Contest : 3 original 100% ham brewing over 5 projects.
Need a general purpose high end instrumentation gear ? check the N2PK web site.
Want a cheap way to play with GnuRadio and SDR ? Google for “Hermes-lite” and read the github p0rn files. Not powerfull enough ? try to build a full fledge Hermes (Anan) 200 W rig. The main pcb costs less than 20 bucks.
Wana try a more traditional approach ? look for the word “picastar” (150 W PEP, 1/30 MHz)
Wish to build a veeeeery easy SDR tranceiver ? seek “Softrock”. Not powerfull enough ? try to extend it with a Mobo 6.3 and an SDR-Widget etc.
dreaming for 1 MHz to GHz low cost rig ? the UHFSDR is for you…. you’ll only need some Mitsubishi hybrid amp to run 70 W
… and all of this is an extremely small view of the homebrew domain. Once you have entered in this third dimension, you will see that you’ll need many lifes to realize all the projects you’ll intend to launch
Hope you’ll join us
73′
Marc f6itu (noooo commercial stuff in my shack exept my scope and my soldering iron)
Yes, good point. We’ll touch on some of this in Part 2. For completeness could you post links to the 200 watt radio and the 150 watt picastar?
With Pleasure Greg
the last edition of the Picastar is described by VK3PE at
http://www.carnut.info/singleboard/Ver_Porta_P1/Porta_Combo_P1.htm
The Anan is in fact the commercial version of the Hermes, a single board version of the HPSDR made by the Tucson TAPR club (open source, open hardware)
http://openhpsdr.org/hermes.php
the different versions could be seen on the Apache Lab Website
https://apache-labs.com/1001/Ham-Radio-Products.html
the 2 versions of the pcb (called Angelia and Hermes) are sold 18 dollars (not so expensive for a 8 layers pcb of this size).
The different versions of amplifiers, filters etc. are described on the tapr website
ex : http://www.tapr.org/kits_alex.html
and on the Wiki
http://openhpsdr.org/wiki/index.php?title=Main_Page
73′
Marc f6itu
The SDR-Widget is no longer being produced. The Softrock RXTX is a good starting project and performs amazingly well. SDR is the way ahead and total fun as Marc can confirm.
Right now I am putting together Hermes-Lite, a DDC/DUC SDR transceiver and will add a 5W PA later to drive a eb104 PA.
Though these projects are basically QRP there is no reason why a QRO PA can’t be added.
I started with Softrock v6.3 and added MOBO v3.6 and moved on up, Softrock RXTX, UHFSDR, SR63ng + Mobo + SDR-Widget, HiQSDR, openHPSDR Hermes + 300W PA and soon to power up Hermes-Lite the aim of which is to produce a HPSDR Hermes clone for ~$150 based around the BeMicro SDK or CV and AD9866 chip.
When I look at the transceivers I built a few decades ago, including a solid state rig driving a solid state 200W PA, I wouldn’t contemplate tackling such an analog rig again.
Ageed Sid
you’re right.. George stop the production of the widget some time ago. If forgot this detail.
Il also forgot to mention that most of the today’s “analog looking homebrew rigs” are in fact SDR. At least for the receiver, for a pure question of dynamic and performance in term of signal treatment (the picastar, the CDG2000 too, which is a I/Q based XMTR)
http://warc.org.uk/?page_id=81
I wish long life to Gregory’s project
Marc
Hi Marc – I followed the development of the PIC-A-STAR in Radcom but I never thought of building one as modern DDC/DUC rigs are far less involved when it comes to construction time and effort if one can work with SMT components that are getting smaller all the time.
There are parts of the PIC-A-STAR that are still very attractive, especially the PA and filter sections.
My Hermes-Lite is ready for testing and when that is up and running I have another one to build up from bare PCB.
Hi agn
My Hermes-lite is ready to go, but I still haven’t bought the Altera SDK. :-( Shame on me
I’ve jumped in the picastar bandwagon because it’s a really “heavy” project (around 2800 smt components) that teached me quite a lot.(http://wiki.electrolab.fr/Projets:Lab:2011:Picastar). Almost 2 years before hearing something. And a very good Platform to drive the PA3AKE front-end filters and H-mode mixer. But you’re definitely right, this kind of technology is totally “has been” and obsolete. It’s only quality is that after the last drop of solder, you really know what mean the words “mixer”, “gain”, “impedance”. I expect the same with Gregory’s project.
Hi Marc,
I got a SDK from the States and a spare CV from Jim Smith which I decided to use for this build.
Tonight Hermes-Lite is up and running using g0orx.openhpsdr x86 with Android-4.4 in VirtualBox on openSUSE.x86_64.
Receiving clean CW on 40m.
Total build time less than 4 hours.
Still amazed at the marvel of SDR after this long time building and using them.
CW designs are many because they are very simply and easily (cheaply) built, but there are also many, many SSB designs out there for homebrewers. A very popular one is called the BitX. The original was designed by an (east) Indian ham named Farhan. He designed it so it could be built will parts commonly available in India. Of course, there’s much more commonly available elsewhere, and the BitX has become the basis for dozens of variations, including versions for 20 meters. There’s a few Yahoo groups for it. QST Magazine has run a number of design contests in the last several years that included easily-built SSB rigs–some for as cheap as $50USD in parts. There are lots of Yahoo, Google+, and other groups on the web. Once you hook into them, they lead you to many more.
One other point: The only difference between a QRP design and one with higher power is the addition of an amp stage (and final low-pass filter) for which there are a vast array of designs. –Todd
You might find this interesting:
http://soldersmoke.blogspot.com/
There are a lot of non-appliance amateur radio operators out there. Maybe not in your neighborhood, but world wide – its thousands.
I agree. I have been a ham for 60 years. Newer hams buy their equipment. I built mine when I started, and still build gear. I have a homebrew linear, and a homebrew antenna tuner. I intend to build a cw transmitter, and a receiver, as if I was just starting again. There are few decent projects anymore.
I love the idea of the “tuna can” qrp cw rigs…. take something tiny that you built out of a backpack in the woods and “talk” to the world on it…. i have zero desire to “dih-dah-dit” though……
Maybe if i build it, i’ll get more interested in it…. ;)
In the meantime, i’ll keep looking for phone kits…
N1NJI
Done – bitx40, pre-built board, just add case, power supply, and antenna – $45 incl. s/h
http://www.hfsigs.com/buy_paypal.html
Enjoy!
>
My friends and I are building space satellites. If you’re going to Hamcation, there will be a TAPR/ORI series of programs, I think on Saturday.
Solid State Design for the Radio Amateur, great book indeed, but… ouch!
Prices on amazon: used from $100.94, new from $298.98 !!
That’s in my very humble opinion the best argument in favor of piracy.
I was so happy to buy both the ARRL Handbook and the great EMRFD among other books in legit dead tree form although they’re very easy to find as pirated PDF, which I already had, but have no regrets at all for downloading the above book for “free”.
When will they learn that people actually WANT to buy books? But at those prices… sorry but no thanks.
Try http://www.n5dux.com/ham/files/pdf/
Thanks so much for that link! What an incredible source of article!
New? I’m pretty sure that book is out of publication and ‘New’ just means that it sat on a shelf somewhere for a very long time unsold.
In recent years it has come into demand as people who ‘cut their teeth on it’ decads ago have come back to the hobby and are looking for their old, familiar book. In other words it only exists in limted supply yet is in high demand. That’s why it’s expensive.
Don’t get me wrong, I’m sure it was and is great but it is still old. At the very least you are likely to run into problems with parts that are hard also hard to find as they are no longer in production either. My understanding (with limited actual experience) is that EMRFD is supposed to be today’s ‘replacement’ for SSDRA and is the more practical choice anyway since it will use currently available parts. SSDRA on the other hand has great nostalgia value and familiarity to people who started with it decades ago.
So.. complaining about it’s price is kind of like complaining that an old, perfect condition tube radio is expensive when all you really want to do is listen to some music. Just pay for the newer one and don’t worry about it!
Unless someone with great familiarity with both SSDRA and EMRFD can explain why SSDRA is objectively better…
Heck yeah! I built a 20M SSB solid state QRP transceiver out of QST back in the 90s.
Amatuer Radio inspired my interest in electronics. Keep it up on this article and more like it!
Interesting (from a non-ham [yet]). One little duplicate “Amp2” times two in the IF signal chain of the SSB Receivers diagram, but not enough to misdirect the meaning in any way.
I liked the article, and look forward to updates. I did have one minor technical quibble, however. When describing the operation of the product detector, the statement is made, “You are listening to the actual radio waves”. In fact, you are listening to a recovered audio signal, just as with non-SSB reception. The difference is that ordinary AM, because it has a constant carrier as part of the transmitted signal, actually mixes that carrier with the sidebands to get the audio signal out. SSB detection has to “add” that carrier in locally (via the BFO), but the process is essentially the same. Not a big deal, but I thought worth clarifying.
Dave, N6AFV
Here is a much easier (and in many ways) much better SSB Transceiver project.
http://www.qrparci.org/qqsample/qqsample.pdf
Further information:
http://www.jessystems.com/LBS_Detail.html
It’s amazing. In the USA, you can take a 35 question multiple choice test, which isn’t difficult (I know a nine-year-old who did it), and get a technician class amateur radio license. This license gives you the legal authorization to design, build, and operate your own transmitter and antenna to send over a kilowatt of VHF or UHF RF power to the moon and back!
But if you’ve got the technical chops to accomplish that safely and successfully, you can probably pass the slightly more challenging General or Extra class exams, and get more privileges on more bands.
There use to be Morse Code tests, but that’s been gone for a while now. Because it’s a traditional mode, and very efficient to use under challenging conditions, Morse Code still has an avid following, but it’s completely optional these days.
It’s true that there are many more “appliance operator” hams than “build from scratch” hams, but there are both types, and many who fall somewhere in between. There are kit builders, modifiers, tinkerers, repairers, those who build only amplifiers, antennas, antenna tuners, etc. Some build digital interface boxes. Some modify surplus military or commercial gear to make it operate on ham frequencies. Some restore antique gear. Some design kit projects for other hams to buy and assemble. There’s no single right or wrong path in the ham radio hobby. It has lots of little niches, and many interesting and knowledgeable people occupying them.
Just to be clear, the “35 question multiple choice test” is a random selection of 35 questions from a pool of 426 questions. It’s not quite as easy as you make it sound. Personally, I’d like to see the pool bumped up to something like a thousand questions with many of them similar to other ones just so that it would be easier to actually learn the material instead of learning the answers.
You’re absolutely right, but to further clarify for the sake of other readers, every one of the questions is freely available on-line, with all of the incorrect answers as well as the correct answers listed. You only need to get 26 right out of the 35. So there are various ways to pass the test. Of course, learning the material is one way, and it’s the way I’d recommend. But many people just commit the test questions and answers to memory with no understanding, cramming them into their brain on test day, and get their license that way.
Many readers of hackaday here have probably already learned much of the electronics portion of the test, and won’t need much help in that area. Other portions of the test concern regulations and practices, and may require a little bit of study.
And yes, I agree with you that it’s now too easy to get a license without learning much material. Like you, I would prefer a question pool that would be too large to easily memorize — the easiest route to a license ought to be via learning the required material.
You are correct, one can cram and learn the answers for the Tech license in short order. Those of us lucky enuf to have an affinity, and a little backgound can rock it in less than 24 hours. I know, I did, and the LEARNing was of the relevant laws and procedures. BTW, I stood and passed the General exam the same evening, with 100%.
I also stood the Extra exam that evening, and failed. The extra exam requires study, and understanding. Yes, you can brute the test, memorize the pool, but I have never met another extra who did so. If you are that committed, you’re interested enuf to dig in and LEARN, not memorize. That took another couple of months….
I’m an “appliance operator”, but I’ve been operating these appliances for around 30 years around the military before I ever dug in and got my amateur license. I too am not too interested in managing the shaky hands and the poor vision I have to build my own rigs…. but I WILL interface them with software, and I’m currently playing with SDR. I think we’re on the cusp of REAL affordability here, time will tell.
In the mean time….
73
K5FQ (currently abroad with no radio)
I studied for a while to pass the General exam (I read the ARRL General study guide several times over the course of six months), and just before taking the exam I downloaded the entire question pool and read each question and highlighted (bold) the question and the correct answer. I the. Read through the highlighted questions and answers twice before taking the exam.
When I sat for my General, I was able to handily pass exam. The VECs encouraged me to try the Extra exam while I was there – it didn’t cost any more, and it would give me an idea what I needed to study for that exam. Well, it turns out I passed the Extra exam by the skin of my teeth, so to speak.
To be fair, I have been interested in radio and electronics since the mid-70s, since I took my first license class for a 5 wpm Novice and studied from the ‘Tune in the world with Ham Radio’ ARRL book – I’m sure that helped… But the Extra exam really felt like a continuation of the General material, there were very few questions I had no idea what the right answer was.
I think a well-prepared Applicant going for their General has a good chance to pass the Extra exam… IF they have a bit of hands-on experience with the material and they are good at standardized tests.
There are over 750 questions in the Extra pool as I recall, to try and brute force it seems like a very, very hard way to approach the material. I thought the material on the Extra exam would be much harder than it actually was, at least on the exam I took.
Informally I studied for 40 years to pass the Extra exam, but I did nothing special to prepare for the exam other than really study for my General exam.
I was 12, my dad gave me the tech-no-code study book and said “the test is this Saturday.”
Great article Greg! Highly recommend the ARRL Handbook! Get a hard-back copy.
Much to the despisement of older hams, I enjoy digital radio the best and prefer to have some sort of computer interface and typing instead of talking or tapping away at a straight key. Something I really want to try is SSTV.
I believe there is an error in the block diagrams of the SSB receiver: After mixing, the spectra shown as LSB and USB are not mirror images of each other.
I’m not sure I follow the block diagrams. I thought USB+LSB = AM. you have to filter out one or the other sidebands.
I don’t know how important filtering out the residual carrier frequency (full suppression) is.
The transmitter is what really confuses me. Without filtering out one of the sidebands, you should get AM and have twice
the spectrum use. (remember when CB had half as many channels ? or how about 23?)
And Drone, those are not upper and lower sidebands of the audio signal, they are upper and lower bands of the
whole band spectrum after the mixer does its thing. Freq + Band, Freq – Band
-G.
Gar,
USB + LSB = DSB or double sideband. AM signals include a carrier + upper and lower sidebands. Your description is of one part of the filter method of SSB generation. If you use a balanced modulator, you generate a DSB signal (no carrier, hence the balanced part), then use a mechanical or crystal filter to remove one of the side bands.
L
Hi, I’m working on a project that requires a signal to be sent to a computer, and I was thinking of building a transceiver to do the job. I virtually have no experience with electronics so any suggestions would be helpful. The signal isn’t meant to carry any information, just to simply alert the computer of an activation at the transceiver location.
“The signal isn’t meant to carry any information, just to simply alert the computer of an activation at the transceiver location.”
That is information.
>
I suppose it is, but I don’t need it to relay any extensive information just a simple ping. I wouldn’t need any type of conversion is the point I’m trying to get across. Thanks for the help.
Great article and I enjoyed the reading.
Having become a CBer in the early 70’s (when I was 17:-) and a First Phone holder in my early 20’s, I had a career in broadcast engineering that fizzled out when the FCC deregulated the industry, eliminating the need for a station to have a chief operator by shifting the responsibility for technical compliance with the rules to the licensee (where it probably should have been all along). Although my father had tried to get me into ham radio when I was in junior high, I wasn’t the bit interested in learning Morse code. I always said I’d become a ham if and when the code ceased to be a requirement. I thought about it when the FCC made us the last country to drop the requirement, but I could never find a VE. Now that I am a semi-retired trucker, I have moved to an area with a very active club with several VEs, and passed element 2 a couple of weeks ago. While I was longhauling, I bought an Icom IC-R70 and separated the twin CB whips on the truck so I could hold the receiver on my leg and explore the bands. I still have the Icom, and my goal is to build a 10 meter SSB transmitter with TR switch to use with it. I’d really appreciate any information that I could get about any such units in use and/or how to build one. I’d also be interested in eventually expanding into all of the SSB HF spectrum as I upgrade through General and Extra, but I’ll probably get there before I get on 10 meters. I’d like to get active as a Elmer and pass on my knowledge to those who want it.
I don’t understand the process of multiplying down in frequency, would it be more correct to divide down, and multiply up?
Steps to build a ham radio from scratch. Step 1: become familiar with the various components of your ham radio. Step 2: obtain a valid ham radio license. Step 3: design and build a working circuit.
You can do amateur radio yourself. Ham radio can be built by anyone with the right tools and resources: a circuit board or a ham radio kit. Aside from that, learning how to start a radio hobby from scratch takes a lot of patience and perseverance.
You must build up a station consisting of the transmitter, receiver, antenna, tuner, and other optional equipment in order to have a DIY ham radio, which is made feasible by ham radio kits.