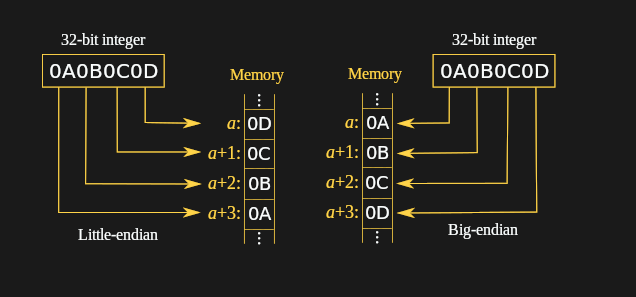
Most of the processor architectures which we come into contact with today are little-endian systems, meaning that they store and address bytes in a least-significant byte (LSB) order. Unlike in the past, when big-endian architectures, including the Motorola 68000 and PowerPC, were more common, one can often just assume that all of the binary data one reads from files and via communication protocols are in little-endian order. This will often work fine.
The problem comes with for example image formats that use big-endian formatted integers, including TIFF and PNG. When dealing directly with protocols in so-called ‘network order’, one also deals with big-endian data. Trying to use these formats and protocol data verbatim on a little-endian system will obviously not work.
Fortunately, it is very easy to swap the endianness of any data which we handle.
Keeping Order
If bits can be packed in either order, it makes sense to tag the data with a marker up front. For instance, in TIFF (Tagged Image File Format) images, the first two bytes of the file indicate the byte order: if they read ‘II’ (from ‘Intel’) the file is in little-endian (LE) format, if they read ‘MM’ (from ‘Motorola’) then the data is in big-endian (BE) format. Since Unicode text can also be multi-byte in the case of UTF-16 and UTF-32, its endianness can optionally be encoded using the byte order mark (BOM) at the beginning of the file.
Although one could argue the need to care about endianness in most code, it bears reminding that many processor architecture in use today are in fact not LE, but bi-endian (BiE), allowing them to operate in either LE or BE mode. These architectures include ARM, SPARC, MIPS and derivatives like RISC-V, SuperH, and PowerPC. On these systems, one can’t just assume that it’s running in LE mode. Even more fun is that some of these architectures allow for endianness to be changed per process, without restarting the system.
Case Study: Dealing with Endianness
Recently I implemented a simple service discovery protocol (NyanSD) that uses a binary protocol. In order to make it work regardless of the endianness of the host system, I used another project of mine called ‘ByteBauble‘, that contains a few functions to easily convert between endiannesses. This utility was originally written for the NymphMQTT MQTT library, to also allow it work on any system.
The use of ByteBauble’s endianness features is fairly straightforward. First one has to create an instance of the ByteBauble class, after which it can be used for example to compose a binary (NyanSD) message header:
ByteBauble bb; BBEndianness he = bb.getHostEndian(); std::string msg = "NYANSD"; uint16_t len = 0; uint8_t type = (uint8_t) NYSD_MESSAGE_TYPE_BROADCAST;
After the message body has been defined, the length of the message (len) is the only part of the message header that is more than a single byte. As the NyanSD protocol is defined as being little-endian, we must ensure that it is always written to the byte stream in LE order:
len = bb.toGlobal(len, he); msg += std::string((char*) &len, 2);
The global (target) endianness is set in ByteBauble as little-endian by default. The toGlobal() template method takes the variable to convert and its current endianness, here of the host. The resulting value can then be appended to the message, as demonstrated. If the input endianness and output endianness differ, the value is converted, otherwise no action is taken.
The other way around while reading from a byte stream is very similar, with the known endianness of the byte stream being used together with the toHost() template method of ByteBauble to ensure that we are getting the intended value instead of the inverted value.
Converting Between Endiannesses
Fortunately, processor architectures don’t simply leave us hanging with these endianness modes. Most of them also come with convenient hardware features to perform the byte swapping operation required when converting between LE and BE or vice versa. Although one could use the required assembly calls depending on the processor architecture, it is more convenient to use the compiler intrinsics.
This is also how ByteBauble’s byte swapping routines are implemented. Currently it targets the GCC and MSVC intrinsics. For GCC the basic procedure looks as follows:
std::size_t bytesize = sizeof(in);
if (bytesize == 2) {
return __builtin_bswap16(in);
}
else if (bytesize == 4) {
return __builtin_bswap32(in);
}
else if (bytesize == 8) {
return __builtin_bswap64(in);
}
As we can see in the above code, the first step is to determine how many bytes we are dealing with, following by calling the appropriate intrinsic. The compiler intrinsic’s implementation depends on what the target architecture offers in terms of hardware features for this process. Worst case, it can be implemented in pure software using an in-place reverse algorithm.
Determining Host Endianness
As we saw earlier, in order to properly convert between host and target endianness, we need to know what the former’s endianness is to know whether any conversion is needed at all. Here we run into the issue that there is rarely any readily available OS function or such which we can call to obtain this information.
Fortunately it is very easy to figure out the host (or process) endianness, as demonstrated in ByteBauble:
uint16_t bytes = 1;
if (*((uint8_t*) &bytes) == 1) {
std::cout << "Detected Host Little Endian." << std::endl;
hostEndian = BB_LE;
}
else {
std::cout << "Detected Host Big Endian." << std::endl;
hostEndian = BB_BE;
}
The idea behind this check is a simple experiment. Since we need to know where the MSB and LSB are located in a multi-byte variable, we create a new two-byte uint16_t variable, set the LSB’s first bit high and then proceed to check the value of the first byte. If this first byte has a value of 1, we know it is the LSB and that we are working in a little-endian environment. If however the first byte is 0, we know that it is the MSB and thus that this is a big-endian environment.
The nice thing about this approach is that it does not rely on any assumptions such as the checking of the host architecture, but directly checks what happens to multi-byte operations.
Wrapping Up
We will likely never see the end of having to deal with these differences in byte order. This both due to the legacy of existing file formats and processor architectures, as well as due to the fact that some operations are more efficient when performed in big-endian order (like those commonly encountered for networking equipment).
Fortunately, as we saw in this article, dealing with differing endianness is far from complicated. The first step is to always be aware of which endianness one is dealing with in the byte stream to be processed or written. The second step is to effectively use the host endianness with readily available functions provided by compiler intrinsics or libraries wrapping those.
With those simple steps, endianness is merely a mild annoyance instead of a detail to be ignored until something catches on fire.















I always find it strange that the normal convention for handling endian-independent code is to test for the endianess of the host and then swapping bytes, when it’s easy to write endian-independent code without reference to the host, by shifting the data directly.
Thus if b[4] is an array of bytes read in from a stream.
uint32_t be=(b[0]<<24)|(b[1]<<16)|(b[2]<<8)|b[3];
Is the big-endian value regardless of what the host architecture is and because the code doesn't involve any branches, will be pretty much as fast as conditionally swapping bytes.
“and because the code doesn’t involve any branches”
The endian test is constant – unless the compiler’s completely stupid, it’ll just choose the correct branch during compilation and insert the correct code, period. The compiler should be able to figure out that it can just bypass the math in your example, too, but an “if/else” expression with a constant result should happen even with the most basic optimization in a compiler.
This is why you use the host-to-network functions in libraries – they don’t do anything if the endianness matches already.
Came here to write exactly this.
If you use recent GCC or clang this will be even faster than swapping bytes conditionally (at runtime) because the compilers nowadays optimize it to mov or mov+bswap on x86 and ldr or ldr+rev on AArch64. And it saves you from word alignment issues if you happen to write code that works on some old architectures.
“If you use recent GCC or clang this will be even faster than swapping bytes conditionally (at runtime)”
So this compiler is smart enough to realize that it can use faster instructions because of what it’s doing, but not smart enough to realize that the test you’re doing is constant?
Depends on what you do with the test result. The code from the article performs the test inside a separate compilation unit, so it doesn’t matter whether it’s optimized or not. The compiler won’t know the result at the point of calling endian conversion methods. If all the code were put inside header file _and_ all the statements with side effects removed (e.g. std::cout) then yes, the compiler would optimize everything nicely. Which IMO proves the point — Julian’s example above will get optimized regardless of how the code is organized, included and built.
For anyone unfamiliar with how the terminology came into being, it dates back to IEN 137 by Danny Cohen of ISI:
https://www.ietf.org/rfc/ien/ien137.txt
The ultimate source of the terms is “Gulliver’s Travels” by Jonathan Swift.
The choice of the terms (as well as the beginning of IEN137) was an intentional play on the silliness of the Lilliputian wars on whether to crack an egg from the big end or the little end – which was itself a play on the silliness of many political disputes.
The choice of big end or little end in computers was a topic quite some argument at the time IEN 137 was written, and it seems that Mr. Cohen had had quite enough of the bickering.
Can we just stop using network byte order for non-legacy purposes? Almost all new chip designs are LE, why would we use BE for a new protocol?
You have to unpack the values no matter what, because they will never map to be aligned once they’re encapsulated over and over. Network order being big endian means the data as it comes in can be switched and partially dealt with quicker, because the most significant portions come in first. Plus it also has the advantage that in an actual wire capture the data’s readable.
I could also make the argument “can we just stop using incrementing-address DMA transfers for non-legacy purposes? Almost all new chip designs handle both directions, why would we not use decrementing-address DMA transfers for a new device?”
If you miss the reference, if you network capture into a buffer in a decrementing address fashion, the data’s now little-endian in memory. Part of the reason why I hate calling network byte order “big endian” is that it’s actually “most significant byte *earliest*”, whereas “big endian” is actually “most significant byte *lowest address*.” Mapping “earliest” to “lowest address” is the actual cause of the problem, and there’s absolutely no reason you have to do that.
In practice, the only thing I can think of that allows dealing with partial bits of data on the network is the actual low level switching of packets. I can’t imagine game devs are very interested in the upper two bytes of a position or ammo count before the rest gets in, and I doubt anyone in IoT is using the high order byte of a temperature without the rest, to save a few uS.
Practicality beats purity, so low level headers should use whatever gives the best latency and bandwidth at the lowest cost, but network byte order makes its way into the application layer at times, even for things that basically nobody deals with at the level of DMA buffers(as far as I know).
I don’t think I’ve ever seen decrementing addresses in a software ring buffer getting bytes from a socket API, that seems like it would be pretty confusing.
“In practice, the only thing I can think of that allows dealing with partial bits of data on the network is the actual low level switching of packets.”
So to be clear, the original poster said “why would we use BE for a new protocol.” ‘New protocol’ doesn’t necessarily mean “over a 100 GbE link” where a few bytes are microseconds. It could also mean an extremely slow protocol for low-power wireless, for instance, where the data rate might be tens of bytes/second. It also could mean something like an I2C, for instance.
And as for “I doubt anyone in IoT is using the high order byte…”? Are you sure? Look at every I2C temperature sensor out there. They all transmit big-endian: integer portion first, fractional last. Why? Because if you don’t need the fractional, you don’t bother reading out the rest.
“Practicality beats purity, so low level headers should use whatever gives the best latency and bandwidth at the lowest cost, but network byte order makes its way into the application layer at times, even for things that basically nobody deals with at the level of DMA buffers(as far as I know).”
Exactly, which means you’re going to end up with a mix of endian-ness no matter what. That was my point, which apparently wasn’t clear. Not that *everything* should be big-endian. Stuff should be whatever endianness makes sense.
“I don’t think I’ve ever seen decrementing addresses in a software ring buffer getting bytes from a socket API, that seems like it would be pretty confusing.”
Sorry, I guess the sarcasm didn’t come across well. The whole confusion with network byte order/host byte order comes because people want an easy “build integer from bytes” function. Networks will tend to want most-significant bytes to come earliest so they can act on them quickly for switching purposes, and possibly for other reasons.
We *could’ve* had an easy “build integer from bytes” function if instead we had “network increment” and “host increment” operations – one subtracted bytes, one added bytes (and a corresponding ‘network indexed access’ and ‘host indexed access’).
Performance-wise this is actually faster, mind you, but as you pointed out (and as I thought was obvious!) it probably would’ve been confusing as all hell. Although maybe not if it was implemented in the beginning, I dunno.
But as it is now: just learn about data endianness and handle it properly.
Arm64 is big endian, between Raspberry Pi and new Macs and most phones I would say that little endian is the one to drop.
I was under the impression that almost all large ARM chips, are Bi-endian, and are mostly used in LE mode?
I thought they were biendian, too? Looking it up it is, it even started exclusively LE and noted predominantly LE sine becoming bi
Source of big end vs.little end:
https://en.wikipedia.org/wiki/Lilliput_and_Blefuscu#Satirical_interpretations
It may be interesting to note that the C++20 standard is just beginning to offer a bit of support here, see proposal P0463: endian, Just endian by Howard E. Hinnant [1] and the documentation on Header at Cppreference [2].
[1] https://wg21.link/P0463
[2] https://en.cppreference.com/w/cpp/header/bit
I wonder if there’s a way to bypass CPU protections by switching endianness
All numbers should be little endian. Why are we still using the inferior method in our lives? (Partial answer: it is a holdover from the right-to-left of Arabic.)
We should start teaching children how to write the numbers in the correct direction. Since we start addition, subtraction, and multiplication from the least significant digit, it will be easier for them to learn.
Added benefit, we won’t need right-justification just to show a math problem when typeset.
Big endian people are just stuck in the past. Live for the future!
Big endian or little endian doesn’t honestly matter all that much.
What is important on the other hand is that we know what order the bytes of a given multi byte value is written in.
From an architectural standpoint it really isn’t any major difference between the two.
And making an architecture bi-endian is very trivial in the vast majority of cases.
The only things that adds complexity would be things like hardware managed function stacks, address pointers, and other such stuff. Though here we can simply toss a coin for one or the other and then just carry on as if nothing…
Making these features bi-endian is fairly trivial as well, but it adds on a tiny bit more control logic and this can impact peak clock speed, and it also slightly increases power consumption. (Since there is a few more transistors in the implementation.)
In the end, the thing of importance is that one knows if a given value is big or little endian, other than that, it doesn’t matter.
And in a lot of cases, knowing if the host is little or big endian actually isn’t important.
Little endian order was/is a necessity of the 8/16 bit architecture of the day… grab the low order byte first … all math starts with the lower byte…
Can any Intel designers chime in ?
solved a very similar problem at work today using htons() and htonl()
What about the PCI bus? Is it inherently little endian, having been born in PC Land then adopted into the big endian Macintosh world?
What we need is Uni-endian. Values that can be read both ways.
Right? Memory space is so cheap these days. Just store them palindromic.
No article on endianness is complete without mentioning the madness of PDP-11’s middle-endian 32-bit values, where 16-bit little-endian words were stored big-endian (2143), and Honeywell Series 16, which had 16-bit big-endian words stored little-endian to make 32-bit values (3412).
One little, two little, three little endians,
four little, five little, six little endians.,.