DreamWire is a system for generating multi-view wire art using machine learning techniques to help generate the patterns required.

What’s wire art? It’s a three-dimensional twisted mass of lines which, when viewed from a certain perspective, yields an image. Multi-view wire art produces different images from the same mass depending on the viewing angle, and as one can imagine, such things get very complex, very quickly.
A recently-released paper explains how the system works, explaining the role generative AI plays in being uniquely suited to create meaningful intersections between multiple inputs. There’s also a video (embedded just under the page break) that showcases many of the results researchers obtained.
The GitHub repository for the project doesn’t have much in it yet, but it’s a good place to keep an eye on if you’re interested in what comes next.
We’ve seen generative AI applied in a similarly novel way to help create visual anagrams, or 2D patterns that can be interpreted differently based on a variety of orientations and permutations. These sorts of systems still need to be guided by a human, but having machine learning do the heavy lifting allows just about anybody to explore their creativity.

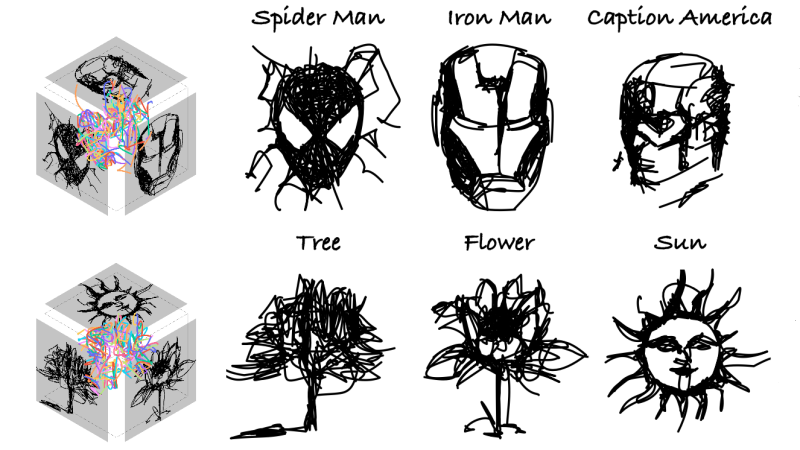














Oh yes, my favorite character, “Caption America”. :)
B^)
Hofstadter did it earlier, and in wood. :-)
Gödel, Escher, Bach 1979
https://en.wikipedia.org/wiki/G%C3%B6del,_Escher,_Bach#/media/File:Godel,_Escher,_Bach_(first_edition).jpg
I had fun in the shop for a while after that, making people’s three initials into 2-inch cubes.
Thank you for that book reference!
https://www.instructables.com/3D-Letter-Cube/
Nice! And now someone needs to make a machine that bends an actual wire to the shape. Might require a few iterations – most likely the shape from the algorithm above is not manufactureable…
Yeah! That’s where it’ll get cool.
I think the number of control points of the Bezier curve is a metaparameter — they could make it smooth fairly easily.
Read the paper more closely — they probably need the degrees of freedom to make the (many, simpler) Bezier curves hook up to make the line continuous.
So might not be as easy as I thought to make it smooth.
first thing i thought of was using it to laser etch inside a glass cube
This is really neat work!
They take a diffusion model, which starts with “noise” and asks how it can improve it to make it look more like a “Caption America” or whatever. Iterate on that until done. (This is like the image generators.)
But here, they do it over parameters of Bezier curves in these three directions simultaneously. Very cool.
I’m trying to think if it makes sense to do this, which is essentially an optimization problem, as a diffusion system or just a regular-old simulated annealing or whatever. I suspect it’s more publishable as a diffusion model. :)
Maybe you recast the problem to be the borders of filled spaces as Bezier curves? But then you’d end up with impossible 3D geometries?
Anyway, a neat problem is half the research. And the G-E-B hat-tip is a nice touch.
Also check this out.
https://files.openscad.org/examples/Advanced/GEB.html