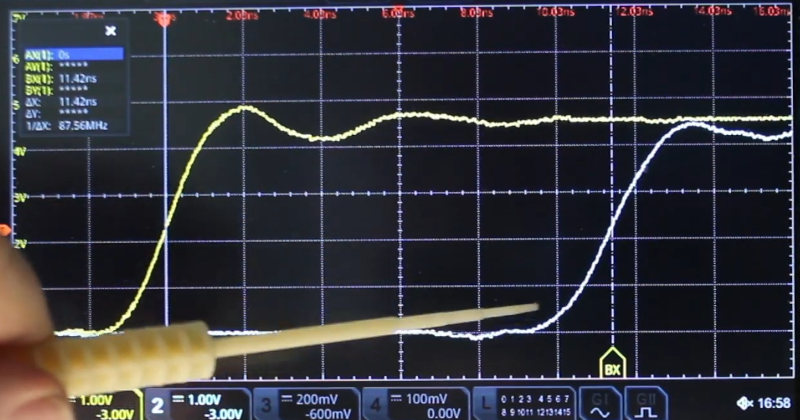
When is the speed of light not the speed of light? Of course, that’s a trick question. The speed of light may be constant, but just as sound travels at different speeds in different media, electronic signals move through transmission lines at a reduced speed. When you have a known cable, you can look up the velocity factor and use it to approximate the length of cable to have a given effective length. But what if you don’t know what kind of cable you have? [More Than Electronics] used a scope to measure it. You can see what he did in the video below.
For example, RG-8/U has a factor of 0.77. Even air isn’t exactly a factor of 1, although it is close enough that, in practice, we pretend that it is. If you wonder why it matters, consider stubs. Suppose you have a 300 MHz signal (handy because that’s 1 meter in wavelength; well, OK, pick 299.792 MHz if you prefer). If you have a quarter wavelength piece of coax shorted at one end, it will attenuate signals at 300 MHz. To understand why, picture the wave on the stub. If the close end of the stub is at 0 volts, then the other end — because it is a quarter wavelength away — must be at the maximum positive voltage or the minimum negative voltage. If either of the extremes is at the close end, then the far end must be at zero volts. That means the maximum current flows only when the signal is at 300 MHz.
If there were no velocity factor, then the length of the stub would be easy to compute. Just take a quarter of a meter or 25 cm. However, since the signal slows down in real coax, the actual stub needs to be shorter by the velocity factor. So, a practical stub made with RG-58 would be about 16.5 cm. Of course, if you can measure the delay with a scope, as seen in the video, you can compute the velocity factor which is good if you don’t know it or you suspect a cable is a bit off.
We’ve looked at velocity factor before. Stubs are more common at microwave frequencies, but you can use coax to build them at lower frequencies, too.
















Lots of technical EE terms in this article. Would be nice for non native (English/EE) to get a simple translation :(
What we call “the speed of light” is actually the speed of light in a vacuum – this is constant. In other media it travels more slowly. In optics this effect gives rise to what we call refractive index. At lower frequencies (in transmission lines like coaxial or twisted pair cable) we talk about velocity factor instead. This is just the ratio of the speed in that medium relative to in a vacuum. Coaxial cable typically has a velocity factor around 0.7 ish (2/3 is often used for a rough figure). Like light, radio waves travel at the speed of light in a vacuum. In the cable, though, the effective speed of transmission is actually more like 200 million m/s instead of 300 million m/s.
Often we don’t care how long a signal takes to travel down a cable, but in some cases it is important. The example given is where a stub is being used as a notch filter. In this case we want the stub to be the right length so that some of the signal we want rid of travels down it, reflects off the short circuit at the end, travels back and ends up exactly 180 degrees out of phase to cancel out the rest of it. This means the stub has to be exactly one quarter wavelength long (so that we have half a wavelength in total – there and back), and because distance = speed x time we need to know the actual speed of propagation in the cable to calculate that length.
Not all heroes wear capes!
Thanks for a great explanation.
It’s a technical subject..
And you can explain technical subjects without domain specific neologisms
Next, make a coax with multiple tap points, so you can use it to select the frequency you want to look at, like an acoustic flame tube.
The reflections could be difficult to deal with, but that’s a really interesting idea
Such things exist. They are called Slotted Lines https://en.wikipedia.org/wiki/Slotted_line.
I used them in my university transmission line lab. They were common in the early days of radio engineering before network analyzers were available. Or today for microwave analysis where network analyzers are very expensive.
I haven’t watched the whole video, but did he make a channel deskew at the beginning? I mean, he measures time differences between two channels in the nanoseccond range.
Is it Schroedinger’s photon or is it Heisenberg’s photon?
Can’t rightly tell.
“When is the speed of light not the speed of light? Of course, that’s a trick question. “
I’m still playing with the thought of making bandpass filters for my cheap Chinesium handheld amateur band transceivers. Using coax stubs might be the way to go.
Bandpass? I don’t know that is easily possible. Stubs are notch filters, they don’t attenuate more than one narrow frequency. I am not the expert and this class was about 40 years ago for me. Does anybody know about making more than a single notch with reflective elements?
16.5÷25 = 0.66 . Is this the real vf of the coax?