Once the domain of esoteric scientific and business computing, floating point calculations are now practically everywhere. From video games to large language models and kin, it would seem that a processor without floating point capabilities is pretty much a brick at this point. Yet the truth is that integer-based approximations can be good enough to hit the required accuracy. For example, approximating floating point multiplication with integer addition, as [Malte Skarupke] recently had a poke at based on an integer addition-only LLM approach suggested by [Hongyin Luo] and [Wei Sun].
As for the way this works, it does pretty much what it says on the tin: adding the two floating point inputs as integer values, followed by adjusting the exponent. This adjustment factor is what gets you close to the answer, but as the article and comments to it illustrate, there are plenty of issues and edge cases you have to concern yourself with. These include under- and overflow, but also specific floating point inputs.
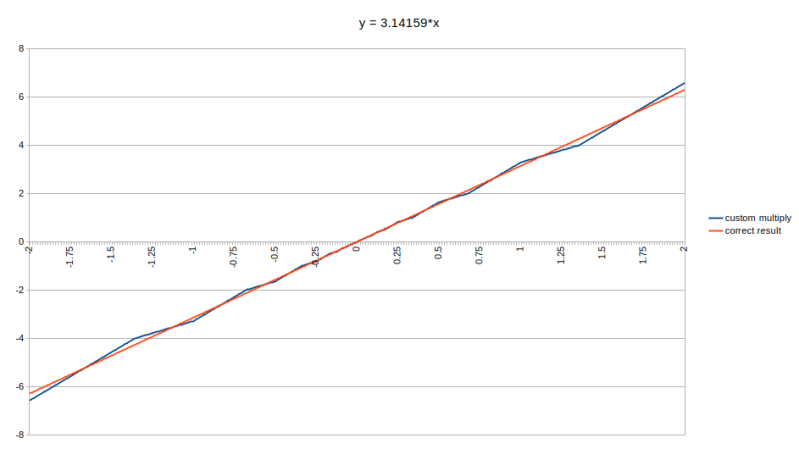
Unlike in scientific calculations where even minor inaccuracies tend to propagate and cause much larger errors down the line, graphics and LLMs do not care that much about float point precision, so the ~7.5% accuracy of the integer approach is good enough. The question is whether it’s truly more efficient as the paper suggests, rather than a fallback as seen with e.g. integer-only audio decoders for platforms without an FPU.
Since one of the nice things about FP-focused vector processors like GPUs and derivatives (tensor, ‘neural’, etc.) is that they can churn through a lot of data quite efficiently, the benefits of shifting this to the ALU of a CPU and expecting (energy) improvements seem quite optimistic.















Neat math trick.
I recently learned about Q numbers (Qm.n and sQm.n) used for fixed precision computing, and the related fixed precision arithmetic that is used with Q numbers. Possibly more interesting and accurate than integer addition?
floating point is really just fixed point with extra steps. fortunately most of those extra steps (as well as the ones you already had to deal with) are automatically handled by the fpu. code long enough and you will break float. if you do fixed point, you know why.
No, the key here is turning multiplication into addition. Multiplication is always a square complexity (just think about the way you do multi-digit multiplication on pen and paper, it’s obviously square), addition is linear. Using fixed point instead of floating point doesn’t change mults to addition.
The reason this works fine with small floats is just that the only part of float multiplication that is actually multiplication is the mantissa (fraction) multiply, and small floats (especially the insane ones used in LLMs) have so few bits to the fraction, who cares. Like, if your fraction only has 3 bits (so only 0.125, 0.25, .. 0.75, 0.875) if you just ignore the multiply you can’t ever be that far off anyway.
Really the whole thing pretty much tells you that LLMs basically only work in log space anyway, they don’t care that much about the actual values as much as log(value).
The article (not the paper) also explains the floor-shift method for log2 approximation, which you can do in a microcontroller or FPGA easily. For 8 bits, think of it like this: start with an 8-bit value A, and an (initially zero) value B, plus an (initially zero) counter C. Shift A.B right – if A is zero, stop. Otherwise increment C and repeat. Now C.B is a Q8.8 approximation to log2. It works because it’s a piecewise-linear approximation between powers of 2 (which he shows in that plot, although it’s more obvious if your span is larger).
Shudders in CS degree and numerical methods minor
This kind of math was what had to be done all the time in early to mid computer graphics. Converting floating point data in a way that can be processed on int only processing chains. It great to see new uses for old techniques.
I wonder if instead of trying to mimic floating point formats, they could just store logarithm of the values with some suitable base that gives enough resolution. Multiplications would become additions, but additions then requires approximation with log(x+y) = log(x) + log(1+y/x)
Well, since 0 is probably the mostly used number and computing an division is probably the hardest operation in an ALU, using log directly isn’t very useful. In a way, a FP number is a log number since it’s storing the exponent in one part (which is the log of the number) and the mantissa in another part (which is the usual number we are dealing with), but it’s done smartly and, better, it’s standard.
“Well, since 0 is probably the mostly used number”
Zero has a special case representation in float anyway, so if you were trying to make hardware that handles stored logs it wouldn’t be any harder. Special-casing a mult or add with zero isn’t exactly a challenge.
And adding really wouldn’t require a division, really you just take the larger of the two numbers and adjust based on the integer part of the second, which is the equivalent of a small float anyway (e.g. a+b = a if b/a is less than the resolution of your mantissa).
” but it’s done smartly and, better, it’s standard.”
(glances at the huge number of new float types)
are you sure
This was the very same idea Yamaha used in their DX7 synths oscillators.
“…the benefits of shifting this to the ALU of a CPU…”
I suspect that it’s less about using a CPU than it is for using few gates and less energy.
Notionally you could produce an NPU much more cheaply and/or larger, and maybe we won’t need to have to fire up 3 Mile Island to feed the data center, either.
i don’t know enough about how the magic of floating point multiplication works out in a cpu.
Multiplication is just recursive addition, a single bitshift can multiply/divide by two. but if integer is still faster than floats you could multiply by 10 until the decimal is gone and then do the operation as an integer, then divide by how ever many iterations of 10 you multiplied by getting rid of the decimal.
with division being “destructive” you could potentially wind up splitting a number and wind up in a with recursion and you’d have to set a precision floor to trim to break out of the loop.
if multiplying out your decimals pushes your number out of 32 bit or 64 bit space, you could always concatenate it across memory addresses or multiple registers in the cpu and chunk through the numbers long division style swapping out the significant bits in and out as you go.
theres probably some specialized formula that could blow all my theorizing away, or a magic lookup table of hacks thats implemented in hardware.
but you could totally get it narrowed down to nX instructions per float operation that scales linear based on how massive your input numbers are.
of course multiplying a float by 10 is still a floating point operation =(
i’m pretty sure there’s a low or high bit that stores the location of the the decimal and that would allow you to iterate or mask out the decimal. but that part might be where the magic of higher math comes in.
The mantissa will speak with you now