The start of World War II threw quantum theory research into disarray. Many of the European physicists left Europe all together, and research moved across the ocean to the shores of the United States. The advent of the atomic bomb thrust American physicists into the spotlight, and physicists began to meet on Shelter Island to discuss the future of quantum theory. By this time one thing was certain: the Copenhagen interpretation of quantum theory had triumphed and challenges to it had mostly died off.
This allowed physicists to focus on a different kind of problem. At this point in time quantum theory was not able to deal with transitional states of particles when they are created and destroyed. It was well known that when an electron came into contact with a positron, the two particles were destroyed and formed at least two photons with a very high energy, known as gamma rays. On the flip side, gamma ray photons could spontaneously turn into positron-electron pairs.
No one could explain why this occurred. It had become obvious to the physicists of the day that a quantum version of Maxwell’s electromagnetic field theory was needed to explain the phenomenon. This would eventually give rise to QED, short for quantum electrodynamics. This is a severely condensed story of how that happened.
Quantum Fields

It’s easy to visualize what a particle is. Visualizing fields is not so easy as they cannot be seen with the unaided eye. They are, however, just as real as particles in every sense. We’ve all felt the repulsive force of two like poles of a magnet. Many of us have sprinkled metal flakes over a piece of paper to visualize the magnetic field of the magnet underneath it. When you rest your hand on a table, your hand is not actually contacting the table. The electrons in your hand repulse the electrons in the table — just the same as like poles of a magnet do. That force is a barrier between your hand and the table, or anything you grab or touch for that matter. Fields are very much a part of our reality.
During the first Shelter Island conference in 1947, it was assumed that the electromagnetic field, photons and electron/positrons were all related to each other in some fashion. Quantum mechanics could deal with photons and electrons, but it was yet to be able to deal with them turning into one another. It became apparent that fields were actually more fundamental than particles, and that particles could be thought of as the ‘quanta’ of the field associated with it. For instance, the photon could be thought of as the quantum of the electromagnetic field.
Early attempts at a Quantum Field theory ran into major hurdles. The equations were based on a perturbation expansion. This is a complex math that is well beyond the scope of this article. But to summarize so you have a vague idea of what happens, an equation is written in a zero order, where it can be solved exactly. Then additional terms are added to form a power series, so you have a first order, second order, third… etc. Each series provides a smaller and smaller correction to the zero order result. When everything is over, the accuracy of the final result is dependent on the number of orders (perturbations).
Early QED equations predicted infinite corrections in some cases. This was due to treating particles as points, without volume or shape, which is essential to quantum mechanics. There was no clear solution. It would take an eccentric American physicist to paint a clearer picture for all to see.
Feynman Diagrams
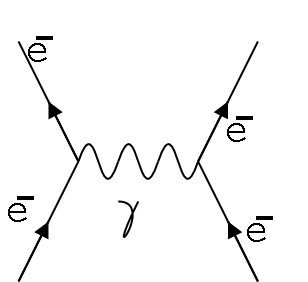
Richard Feynman and a few other physicists were in a race to solve the infinite correction problem and get QED back on track. While others were locked into rigorous mathematical structures, Feynman preferred a more pictorial approach. Basically, he was visualizing particle-photon interaction with a sort of 2-dimensional graph approach. This did not sit well with many of the other physicists, as it seemed Feynman did not understand the uncertainty principle. But his genius was obvious, as he was able to come to the same conclusions that the others did without the rigorous math, so they listened to him. His pictorial approaches were called Feynman Diagrams, one of which can be seen to the right.
They have two dimensions: time and space. Time is the y axis and space is the x axis. There are particles that come in, which are angled toward the center of the diagram. When they change into something else or interact with another particle, they change angles to move away from the center. The changes in particles are caused by a force carrying particle, known as virtual photons or gauge bosons. The force carrier particles are represented by squiggly lines.
To explain the repulsion of electrons for instance, we have two electrons coming toward each other. When they get close enough, a virtual photon is exchanged between them, giving them the information to repel. And then they move away from one another.
Virtual Particles?
Virtual Particles are a key component in quantum electrodynamics. They’re virtual in that they cannot be detected. They are the force carrying particles that allow electrons to repel and allow protons to bind together in the nucleus of an atom. A free electron is actually surrounded by virtual particles created by interactions within its own electromagnetic field. Virtual particles can be created and destroyed without the constraints of conservation laws thanks to Heisenberg’s uncertainty principle. Photons and electron/position pairs can be created “out of thin air” so long as the energy can be accounted for within the time frame determined by uncertainty.
And that’s how QED got off the ground. Richard Feynman and his diagrams, virtual particles and perturbation expansions. QED consists of interactions between particles and virtual particles, which are represented mathematically as corrections in a perturbation expansion, which can be understood more easily with Feynman diagrams. In the next article, we’ll go into a bit more detail about the particles themselves — the six quarks, the six leptons and the four force carriers which make up the mighty gauge bosons. This is essential for understanding QED in more detail. Stay tuned!
Sources:
The Quantum Story, by Jim Baggott. Chapters 18 &19 ISBN-978-0199566846

















Before anyone says this isn’t a hack, Feynman Diagrams were, by the standards of the field at the time, a true hack. Niels Bohr hated them outright and was very dismissive of them and Feynman initially.
I’m 100% in favor of purely educational articles.
When I say “not a hack”, it’s usually because someone decided an art student’s sculpture needs a write-up because they used Solidworks.
Theoretical physics at the early part of the 20th century was awesome. It was honestly filled with people just hacking around with math. Dirac started using the delta function in the 1930s, even though there was no good math backing up what he was doing. The “correct” equations blew up in 4 dimensions, so people said “let’s… just see what things look like if we’re arbitrarily ‘close’ to 4 dimensions, and figure it out later.” Other equations ended up with an integration constant that should’ve been gigantic, so you just said “yeah, that’s our new zero” and worked from there.
The more i read about quantum physics the more it looks like a religious sect ;)
A religious war will come with the GNU/Hord quantum computer..
GNU/Hurd… but Hord works as well..
I’d just like to interject for a moment. What you’re referring to as quantum physics, is in fact, GNU/quantum, or as I’ve recently taken to calling it, GNU plus quantum. Quantum is not a set of physics unto itself, but rather another free perspective of a fully functioning GNU universe made useful by the GNU particles, equations and vital quarks comprising a full universe as defined by Carl Sagan.
Many physicists theorize a modified version of the GNU system every day, without realizing it. Through a peculiar turn of events, the version of GNU which is widely used today is often called “quantum mechanics”, and many of its users are not aware that it is basically the GNU system, developed by the GNU Project. There really is a quantum physics, and these people are using it, but it is just a part of the universe they are in.
Quantum physics is the theory: the model in the universe that explains subatomic particle behavior for the other equations that you use. The model is an essential part of a a universe, but useless by itself; it can only function in the context of a complete universe. Quantum physics is normally used in combination with the GNU universe: the whole system is basically GNU with quantum physics added, or GNU/quantum. All the so-called “quantum” theories are really expansions of GNU/quantum.
Not being a smoker of the ganga, I have never been able to follow Sagan or GNU physics.
It’s legal in some places – wrap one up & get on-board.
I literally laughed.
I’m a quantum atheist. I reject all things involving quantum theory until there is some evidence that it actually works. Semiconductors are a great start. That EM drive is looking promising but I’m not convinced yet.
I’ll believe in quantum computers when one of them is running DOOM II, and I’ll believe they can be practical when they can boot Linux. Until then, a $10bil liquid hydrogen-cooled device only capable of 4-bit operations may as well be a couple transistors.
So you don’t believe in scanning-tunneling electron microscopes or superconducting quantum interference devices (SQUIDs)? Both of those are practical devices which are fundamentally based on quantum mechanics, which manifestly “work.”
The EM drive has nothing to do with quantum mechanics. Please don’t include it in the discussion.
I believe in those things because they exist and are practical. Quantum computers do exist now, but for the massive expenditure of energy are less functional than a 7400 quad NAND IC.
As for the EM drive, every explanation I’ve heard for it involves either quantum vacuum or quantum foam, whatever those are. It’s not my field so I await an industry application for the theory and until then it’s just nonsense from an engineering point of view.
So what the heck does being a “quantum atheist” mean? It sounds more like you just disbelieve quantum computing hype. Which is fine, but jeez, that’s disbelieving a marketing person rather than fundamental physics.
I can’t reply to your lower comment directly.
>So what the heck does being a “quantum atheist” mean?
It means a joke. Humor.
It’s a bad joke, because the only thing you apparently don’t believe in is the hype for quantum computers. And the hype for something has nothing to do with the underlying physics.
> I’ll believe in quantum computers when one of them is running DOOM II, and I’ll believe they can be practical when they can boot Linux
You’re either trolling or have no idea how quantum computers work.
You have doubts about quantum theory until you try to study it. Then you can have one of two states. You believe it or you don’t believe it, but you can only be sure of one of those.
This is what I believe is termed ” the quantum uncertainty principle” :)
Interesting article, thank you for writing it and including it here!
I look forward to more articles like this.
Spooky articles at a distance..
Leave us be, Einstein!
Someone needs to put pilot wave theory to perspective too.
I really don’t agree with a few ways things are characterized here.
First, quantum mechanics had fields as well. Of course it did – you had a wavefunction, which had a value at every point in space and time. That’s a field. They just weren’t *relativistic* fields. You always had particles being quantized excitations of the wavefunction (its eigenstates).
So what quantum field theory, and quantum electrodynamics is, is just relativistic quantum mechanics. That’s why quantum field theory was developed, because electrodynamics is the only relativistic thing that we encounter literally every second of our lives. And making a relativistic version of quantum mechanics was really, really hard.
In order to make those quantum mechanical wavefunctions relativistic, you ran into a bunch of problems. Fractional spin, for instance, becomes a huge problem when you can just move from a frame *behind* an electron to one *in front* of it, and the spin direction changes. So you had to treat objects with fractional spin differently (“spinors”), which generated an entirely different mathematics (the Dirac equation, rather than the Schrodinger equation), and suddenly predicted both “positive energy” and “negative energy” solutions.
And the *big* problem with the Dirac equation, its Lagrangian formulation, and the associated math was that you couldn’t solve it. There was, literally, no way to solve it. So you had something which *looked* right, which *felt* right… but couldn’t be used. So people started to do approximations.
And that’s what Feynman figured out. Not Feynman diagrams, which are just ways to *draw* an equation compactly, and super-helpful in trying to convey a ‘feel’ for what’s going on, but ultimately not really physics. Feynman figured out how to *efficiently approximate* answers, with progressive accuracy – specifically, Feynman parameters really helped to actually solve very, very nasty path integrals. Feynman diagrams are essentially ways of nicely grouping those approximations (into leading order, next to leading order, etc.) so that they can be individually attacked.
—
The other problem I had was the idea that a “virtual particle cannot be detected.” That’s not what a virtual particle is, and you can absolutely detect them, without a doubt. A virtual particle is really easy – it’s an excitation of the field that can’t propagate over large distances.
This is easy to understand – imagine if you drop two rocks in a pond, separated by 10 feet. You’ll see nice ripples radiate out from each of them, then they’ll cross, and interfere in an easy-to-understand pattern. Focus on the line directly connecting the two rocks. Those are propagating waves. Now do the same thing, but only separate the rocks by, say, half a foot. Again, pay attention to the line directly connecting the two rocks – and this time you won’t see *anything* that looks like a propagating wave. It’s just a mess. And in fact, at far distances you won’t see two propagating waves at all – they’ll basically merge into one. That “mess” between the two rocks is what a virtual particle is.
The interesting point here is that there’s no real distinction between “real” and “virtual” here. It’s a smooth transition, as you bring the rocks together. Same thing in particle physics. Virtual particle just means it doesn’t propagate to infinity, so technically *everything’s* virtual. But practically, the difference between an infinite propagation and any macroscopic propagation is negligible.
A wave function might be thought of as a probability field for the purpose of computation. You think it is a physical field?
The wavefunctions in non-relativistic quantum mechanics are exactly the same fields that are used in the Feynman diagrams. They just stop using the psi symbol because there are now interacting fields, so you need multiple symbols to distinguish them.
But they’re exactly the same deal. There’s no difference between the electromagnetic field (which you’re used to) and a lepton field (which is that wavefunction from quantum mechanics).
So yes, it’s a physical field in the same sense that the electromagnetic field is a physical field. If you want to view it as a probability density distribution, you can do that for the electromagnetic field, too. It’s now the probability that a photon will scatter off you and the particle a distance away that’s generating it.
So basically what you are saying is “virtuality” vs “reality” is just ratio of wavelength to a distance?
But then does it mean that e.g. electrostatic force uses virtual photons of successively greater wavelengths as two electrons are pushed further apart? Is the explanation of inverse square law in Max Planck’s postulate that higher wavelength carries less energy? And the fact that electrons can’t fall to nucleus and push each other out from shared orbitals, does that mean that there is hard lower limit for the wavelength of a photon?
Does it also mean that short-range forces, like weak and strong interactions simply don’t have particles of varying wavelengths (or have hard upper limits to their wavelengths)?
Does that mean that gravitons should also have potentially immensely huge wavelengths?
Does “dark energy” exist because there is upper limit to wavelength of graviton as well?
“So basically what you are saying is “virtuality” vs “reality” is just ratio of wavelength to a distance?”
Kindof. It’s how far “off-shell” the particle is – that is, how closely its energy matches its mass/momentum. It’s called “on-shell” because its energy/momentum form a 4-vector, and the length of that vector should match its mass. So its mass defines the shell of a 4-sphere. Don’t try to visualize it, though, because Minkowski space is weird.
How far off-shell you are relates to the interaction time, and therefore the interaction distance, via Heisenberg’s relation.
“But then does it mean that e.g. electrostatic force uses virtual photons of successively greater wavelengths as two electrons are pushed further apart?”
It uses photons of successively greater wavelengths. Specifying virtual here is redundant, since any particle that’s exchanged between two others must be virtual, although at large distances they become arbitrarily close to on-shell.
“Is the explanation of inverse square law”
At large distances when you really *have* to be essentially on shell, the energy’s density’s just spreading out over time over a shell, hence, inverse square. At *short* distances, though, you don’t even have an inverse square law. The force between 2 electrons doesn’t follow an inverse square law at very short distances.
Orbitals in atoms show up because of the spherical geometry. You’re also making a common mistake about atoms – in a hydrogen atom, the place you are *most likely* to find an electron is *inside the nucleus*. That’s where the electron spends most of its time. (This is not the *radius* you are most likely to find an electron at, but that’s because larger radii encompass more area).
“Does it also mean that short-range forces, like weak and strong interactions”
No to the strong force. Strong interactions have multiple ‘charges’ (red/green/blue), and so that changes the entire dynamics of the situation. Instead of having one chargeless mediator (the photon), you’ve got 8 different mediators, all of which *do* have charge, so as distance grows the force gets *stronger*, because there’s more color around you. Strong interactions end up being *weak* at short distances. Think about it in comparison to electrodynamics. Imagine if you had *electrons* radiating out from a point, rather than photons. The field would get stronger as you were farther away.
Yes to the weak force. Its force carriers have mass, so they can’t have arbitrarily low energies (hence wavelengths) – they’re bounded by the mass of the carrier. In actuality, they really have mass because they’re the portion of the electroweak field in the direction of the polarized Higgs vacuum. So they *seem* like they have mass because they keep smashing into the Higgs vacuum, which is everywhere. This is the same reason the electron has mass and the neutrino doesn’t (well… mostly doesn’t).
“Does that mean that gravitons should also have potentially immensely huge wavelengths?”
There is no quantum field theory of gravity, and in fact, there cannot be one.
“Does “dark energy” exist because there is upper limit to wavelength of graviton as well?”
Dark energy is just a way of saying that the vacuum has a component with negative pressure (that is, its energy increases as its volume increases), and which couples to both radiation and matter. Other than that, we have no idea what the hell it is.
Thank you for taking time to answer my questions! I looked up the date of comments only after I already posted, and didn’t held hope that I’ll get any response, but this is certainly more than I can grasp at my current level of understanding. We laymen always wish for more simplicity and intuitive understanding, but I guess nature is as nature does and we have to accept that.
I suggest reading Feyman’s book QED.
I think it was to explain QED to introductory physics students, so a lot of HaD would not be lost trying to read it.
+1
I totally agree, but for the TMI (Too Much Information) factor involved.
Based on some of the comments here, it’s not at all clear that some HaD readers would not have a major problem accepting the fact that there are only three forces in nature: the atomic force; gravitation; and quantum electrodynamics.
Well, I definitely would, because it’s completely wrong.
Fundamentally, in the Standard Model, there are 4 fundamental interactions. QCD (strong nuclear), electroweak (the high-energy unification of QED and the weak nuclear force), gravity, and the Higgs interactions. A “force” is anything that exchanges momentum, which is what all of these interactions do.
Conceivably, the Higgs interaction could get grouped into the electroweak part, but that would reduce it to QCD, electroweak, and gravity, but there’s no overriding reason to group it with electroweak. You need it to turn the electroweak force into QED + weak nuclear, but the electroweak part *itself* doesn’t need it. At high energies when the Higgs vacuum energy is negligible, the electroweak part is fine on its own.
However, if you’re grouping terms by ‘interaction type’, you probably would want to have five parts – QCD (the SU(3) color part), weak nuclear (the SU(2)-isospin part), QED (the U(1)-hypercharge part), and the Higgs interactions (mass part).
Oops, that last set should include gravity, in whatever mythical theory can include gravity along with the others.
“Well, I definitely would, because it’s completely wrong.”
Gee, it’s a shame that you said that, because “it” is EXACTLY what Dr. Feynman states in his book ‘QED”.
You DID READ ‘QED’ before you posted your load of useless technobabble above, right?
Because it’s unthinkable, in the field of science, that someone would make claims without at least consulting SOME relevant literature, I am going to the trouble of pointing you to the SOURCE of what you state is “…completely wrong…” :
‘QED–The Strange Theory of Light and Matter’, copyright © 1985 by Richard P. Feynman; seventh printing with corrections 1988.
Now, if your position is motivated by your having a later edition of Dr. Feynman’s seminal work, and this later effort completely retracts everything in QED (©1985), I, and indeed the entire scientific community, would be forever grateful to you for apprising us all of the true state of affairs of quantum electodynamics.
Oh, and you might also consider suggesting to the Nobel prize committee that it should, based on your findings, exercise more diligence, and operate in a less precipitate manner, than it did when awarding Dr. Feynman the Nobel Prize in Physics (with Tomonaga and Schwinger) in 1965, for QED.
It might surprise you to learn that physics has advanced since 1965.
I’m also a physicist, and Pat has done an excellent job of describing things accurately in plain English – it’s one of those rare occasions when someone actually knows what they’re talking about.
Feynman is a pleasure to read but if you are quoting him accurately then that simplification doesn’t make much sense. I did read that book many years ago, and i don’t think that he refers to an ”atomic force ” (wtf is that?) and QED is not a force, although the description does include interactions involving the electromagnetic and weak forces, which incidentally are also my best guess at what you mean by atomic force.
I don’t terribly blame him for the sharp reaction, since really, physics texts approachable by the general public have just completely fallen apart terribly over the past 100 years, and really over the last 30 years, which I think of as the “era of pop-trash science literature.” (No disrespect to the authors of those works, but they’re just feeding a narrative that physics is weird and strange rather than trying to give understanding). So strongly defending wording from 30 years ago isn’t that surprising – there hasn’t really been anything since then that’s well-written enough for an easy understanding.
In fact, the Standard Model always gets advertised on big posters as having “the Four Fundamental Forces”, right? Even though electromagnetism and weak nuclear are the same force, and the Higgs interaction is totally left out (other than saying it “gives particles mass” which… is a seriously lacking description of what the Higgs does). And the argument that “well, it’s only at the highest energies that it’s really electroweak, and most people work at lower energies” is silly.
It’s almost like physics is scared to try to change the pretty picture they’ve presented to the public.
I’m the owner of a blog that follows the development of an E.M propulsion system called PNN.
Its inventor, Emidio Laureti, is convinced that quantum physics isn’t the right path to unveil the principles behind this form of propulsion.
He claims that the key lies behind the displacement current, a blunder that has taken away the opportunity to exploit this phenomenon.
PNN, EmDrive, Cannae drive in fact have one thing in common: they all are capacitors.
https://neolegesmotus.wordpress.com/2016/05/15/asps-position-on-displacement-current/
https://neolegesmotus.wordpress.com/2016/04/04/f242-the-game-changer/
> The equations were based on a perturbation expansion. This is a complex math that is well beyond the scope of this article. But to summarize so you have a vague idea of what happens, an equation is written in a zero order, where it can be solved exactly. Then additional terms are added to form a power series, so you have a first order, second order, third… etc. Each series provides a smaller and smaller correction to the zero order result. When everything is over, the accuracy of the final result is dependent on the number of orders (perturbations).
I think a more intuitive explanation is trying to measure something with only odd length unmarked rulers.
Lets say you want to know how high a ceiling is, you might start with oh well my fridge is 2m tall and the ceiling is about that height.
Then you can add well this box says its 18cm and if you put the two together thats closer so we have 2.18cm
Next I can fit this pizza box in and thats about 2cm so all in all we have about 2.2m
Effectively you are making a initial assessment and then adding smaller and smaller adjustments, eventually each adjustment will be too small to count and you *converge* on a figure.
Thanks Peter, this is fantastic! It’s exactly what I try to do with these type of articles… simplifying them so anyone can understand. If it’s OK with you, I’d like to use this analogy in the next QM article.