When [Thundersqueak] was looking for a project for The Hackaday Prize, she knew it needed to be a special project. IoT devices and microcontrollers are one thing, but it’s not really something that will set you of from the pack. No, her project needed to be exceptional, and she turned to logic and balanced ternary computing.
[Thundersqueak] was inspired to design her ternary computer from a few very interesting and nearly unknown historical computing devices. The first was the [Thomas Fowler] machine, designed all the way back in 1838. It could count to several thousand using a balanced ternary mechanical mechanism. The [Fowler] machine was used to calculate logs, and the usual boring mathematical tasks of the time.
A bit more research turned up the Setun, an electronic computer constructed out of vacuum tubes in 1958. This computer could count up to 387,000,000 with eighteen ternary digits. On the binary machine you’re using right now, representing that would take twenty-nine binary digits. It’s about a 2.5 times more efficient way of constructing a computer, and when you’re looking for the right vacuum tubes in 1950s USSR, that’s a great idea.
[Thundersqueak] isn’t dealing with vacuum tubes – she has a world of semiconductors at her fingertips. After constructing a few truth tables for ternary logic, she began designing circuits to satisfy the requirements of what this computer should do. The design uses split rails – a negative voltage, a positive voltage, and ground, with the first prototype power supply made from a 741 Op-amp. From there, it was just breadboarding stuff and checking her gates, transistors, and truth tables to begin creating her ternary computer.
With the basic building blocks of a ternary computer done, [Thundersqueak] then started to design a basic ALU. Starting with a half adder, the design then expanded to a full adder with ripple carry. We’re sure there are plans for multiplying, rotating, and everything else that would turn this project into a CPU.

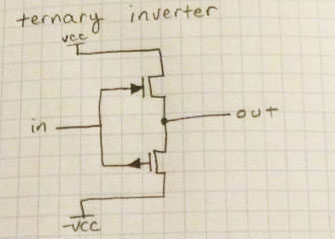














I wonder if you made one with gigahertz opamps or so… there surely are some tri-state microwave buffers which would be usable in this project, no?
“On the binary machine you’re using right now, representing that would take twenty-nine binary digits.” So? Bits are cheap. A raspberry pi has 32, the machine I’m writing this on, 64. A 32 bit machine can count to 4,294,967,295. That’s ~11 times greater than the 18-trit value. Pardon my ignorance, I must be missing something here.
Here’s something to consider: Why isn’t/wasn’t quaternary a thing? I would posit that quaternary being 4-some, didn’t (or can’t) offer anything over binary since 4 is a module (modulus?) of 2.
Still it’s cool! Hat’s off to Thundersqueak for getting far enough with it to do a presentation of that quality and detail. I understand trinary a bit better now.
Yes, bits are cheap, but this method is a lot more efficient at cramming information into less bits. Using ternary bits, a 32-bit system would be able to count over 400,000 times higher.
I’m sure there are many reasons why this didn’t take off, one main one is most likely the fact that binary took off quicker.
http://en.wikipedia.org/wiki/Ternary_computer
Ternary bits are going to be bigger to carry information with the same reliability. In addition ternary logic is going to take up more space, and require more complexity.
There are flash memories that are quaternary (each cell can hold 1 of 4 values) internally. That’s translated back to binary for I/O.
Ternary is more efficient than either binary or quaternary (or any other *nary) for one very simple reason. It is the nearest whole number to the most efficient based that exists… which is e (2.71828…). Since e is an irrational number that cannot be represented in computational hardware, 3 is the next best thing because it is the nearest whole number.
Apparently, Setun used an interesting combination of vacuum tube, diode-transistor and magnetic logic. http://tinyurl.com/l4fwuso is a PDF which has some accounts of the machine.
Specifically, on page 6, “The machine contains 4,000 magnetic cores, 4,000
germanium diodes, approximately 100 transistors, and 40 vacuum tubes.” And on page 9, “However, whereas the SETUN uses magnetic circuitry in its arithmetic unit…”
I’d like to see how or if a ternary magnetic logic gate works.
“We’re sure there are plans for multiplying, rotating, and everything else that would turn this project into a CPU.”
Sorry to nitpick, but while bit shift and rotation are rather easy to do (a right shift being particularly useful), I wouldn’t hold my breath on multiplication. Doing multiplication in a single shot takes large numbers of ANDs and adders, regardless of what tricks you use. A single adder could be used if [Thundersqueak] was going the microcode route, but I imagine she’ll just leave out a multiplication instruction and have the programmer use a multiplication subroutine, like in most early CPUs and some microcontrollers.
Of course I have no experience in ternary logic, so I’m working off my binary experience here. This makes me curious: are 3-operand functions (ex. 3 input add) easier in ternary because of the three states?
the curta calculator used nines compliment something for its logic so shouldnt be too hard.
Maybe a good entry would have been to build a wireless mic for handing out to the audience during Q/A time.
That was a consideration we should have thought of. For the next few videos, I might be able to pull audio off the dropcams…
Or, just have presenters repeat the question.
For future events, that is. Unless you’ve a working TARDIS or anomaly generator. (c:
Would booleans be different in a ternary computer? Would they be called trooleans? There’d be some wasted space (or at least extra logic needed) to store it efficiently, think of 24-bit color (8 bits for each of the r, g, and b) not really fitting into the 32-bit path. A boolean is true and false, if it’s true, false and something else (half truth??) then we don’t really have a boolean anymore. Think of how important booleans are in computer science. That could answer some question of why ternary never made it– I’m not really buying the notion that binary “just caught on quicker”. There are fundamentals, I believe.
Non-silly 3logic values: T/F/not set or T/F/Error.
Yup, it’s a troolean! Having a third state in a boolean, at best, taints the meaning of true (or false!) and reminds me of PHP’s wretched way of dealing with booleans with all its triple operators, having to use isset() and other programming malpractices. Just one example of the “extra logic” I hinted at. I’m not saying ternary can’t deal with booleans–just not as efficiently as binary.
There’s always the clbuttic True False and File Not Found:
http://thedailywtf.com/Articles/What_Is_Truth_0x3f_.aspx
Booleans are already represented extremely inefficiently most of the time in binary computers; in C and most languages inspired by it sizeof(bool) == sizeof(char) == 1 (i.e. 8 bits). Which is part of the reason for the horror of C++’s std::vector. Fortunately std::bitset eventually came along.
That was supposed to refer to std::vector’s bool specialization.
HaD: Please don’t silently strip out anything that happens to look like an SGML tag. It’s really not that hard to convert >< to ><
> It’s really not that hard to convert ><
lol.
We've got a thing coming. Better 'code' is on the list. Not high on the list, but it's on there.
A negative voltage could work, I’ve pondered this before. But for those suggesting multiple voltage levels, that won’t really work and here’s why:
When you ramp this up to max frequency, that data stream doesn’t look like square waves anymore, you lose the edges. And the data is flying so quickly that you don’t see a full voltage flat spot unless it’s more than ‘1’ in a row. Practically on the verge of ADC conversions happening. This is highly exaggerated with HDD platter reading, they actually do straight up analog to digital signal processing. So you would have to slow things down enough that 1/2 V could be determined as an actual intermediate voltage level vs alternating ‘1’ and ‘0’ bits.
If the only other value to consider is ‘-1’ then this problem doesn’t actually get worse. Probably easier.. but any input capacitance will cause about twice the switching loss, among the myriad of other issues in rethinking conventional logic circuits to accept negative voltages.
I just realized while reading the overview why ternary computing never took off. In a binary system you call each significant place a bit, shortened from binary digit. You’d run into a problem shortening ternary digit in the same way, and no one would take the time to say it the long way.
I have no problem with “tit”.
I think (well I’ll prefer) to call it a ‘trit’
Can you imagine problems with the Computer Architecture classes though? “Alright everyone, your assignment is to design a 16-tit ALU. Any questions?” “Can I bring a friend?”
That happens every single time I try talking about it :p
I think its a huge conspiracy–and all computers are really ternary machines. After all, the ATX power supplies all have a -12v rail that supplies an amp or less. It’s powering the real, ternary computer in there. All them other 5 volt, 3.3 volt rails are just in there drawing power to dissipate through the heat sinks, to cause climate change and help make the power companies more money. It’s repression, man.
Wait… how are you going to output data? Blinkenlights are binary (on/off) and you’ll run into a lot of trouble trying to hook it up to a terminal -unless of course the data is translated back into binary
2 colour leds? Off/Red/Green?
Maybe… or they could use analogue meters to indicate what state its in
That’s how I was doing it on the breadboard, just 2 LEDs setup so that if it was negative one lit and if positive, the other lit. You could also just use a dual color LED, but since I had lots of single color ones that is what I used. I have also made use of an analog multimeter and just watched the needle swing.
I built a ternary computer in 2012 as a 4th year project in my engineering degree. I used an FPGA, which was the enabling technology as well as its limitation.
Despite the academics saying it couldn’t be done, I did.
In the early stages I had studied the Setun, and found it confusing, translated by people who did not understand it.
I reviewed the SETUN again at the end, and it all made sense. We had in fact followed very similar paths.
There has been some misinformation about the SETUN in hackaday pages. It did not used valves. Its memory used two magnetic rings per trit, meaning it ignored the fourth state.
In the early stages where I tested modules, I used LEDs to show states. Off meant N (or -1), Dim meant 0, and full on meant 1.
The completed 12-trit processor ran at 2.5MIPS, and included multiply & divide instructions. I wrote a ternary BIOS for it and used a serial terminal for communicating with it and sending it programs to run.
After graduating I continued with development because it was so interesting.
Currently on the shelf while I work on other projects. I still think ternary is awesome!
Logic takes up very little total die space in our modern computers. Memory consumes most of it. We already have multi-level flash; DRAM and SRAM will probably turn that direction as our silicon process reaches its limits in a couple years.
Ternary logic may well have advantages for multiplication. A ternary encoding called Canonical Signed Digit (CSD) is sometimes used even now on binary computers to speed up multiplication because it minimises the number of non-zero bits. Each digit can have values -1, 0 or 1.
The next step in this project is putting everything together, the parts are on order for this. I am switching over to the DG403 from vishay as it has a similar internal schematic and after playing with some, I think I can make it work. :)
I was looking at old tech a while back and was musing that a magnetic core memory could have been possibly used to store a ternary value, given that you could orient the magnetic field, or simply have it “off” allowing for 3 possible states. As cool as tinkering with recreating a magnetic core ram module would be, I will probably go the transistor route.
Just watched the presentation. Interesting stuff! Your trinary gates have a very “CMOS” look. I’d expect the gates to have a trade off between power consumption with zero inputs, and the stability of zero outputs. Have you considered moving to more ECL style gates? ECL is based around the “long tailed pair” differential amplifier and I’d expect it to be stable with +, -, and 0 voltages. ECL can be blindingly fast, but usually uses a lot of power. Though I have seen one article on using ECL like circuits at low voltages to save power.
i think it’s a great idea, maybe you can make a project on kickstarter,
but i’m thinking about a thing: in theory when you transmit ternary signal you will have probably have some troubles with error propagation, to solve this you can develope a ternary/binary and a binary/ternary converters, or you can just adapt hamming code to the ternary math
About Setun on Russian http://old.computerra.ru/vision/652817/
If you need help to find more information, I can try to help.
https://www.facebook.com/TernarySystem/photos/rpp.400381460357464/401752760220334/?type=3&theater