My DSL line downloads at 6 megabits per second. I just ran the test. This is over a pair of copper twisted wires, the same Plain Old Telephone Service (POTS) twisted pair that connected your Grandmother’s phone to the rest of the world. In fact, if you had that phone you could connect and use it today.
 I can remember the old 110 bps acoustic coupler modems. Maybe some of you can also. Do you remember upgrading to 300 bps? Wow! Triple the speed. Gradually the speed increased through 1200 to 2400, and then finally, 56.6k. All over the same of wires. Now we feel short changed if were not getting multiple megabits from DSL over that same POTS line. How can we get such speeds over a system that still allows your grandmother’s phone to be connected and dialed? How did the engineers know these increased speeds were possible?
I can remember the old 110 bps acoustic coupler modems. Maybe some of you can also. Do you remember upgrading to 300 bps? Wow! Triple the speed. Gradually the speed increased through 1200 to 2400, and then finally, 56.6k. All over the same of wires. Now we feel short changed if were not getting multiple megabits from DSL over that same POTS line. How can we get such speeds over a system that still allows your grandmother’s phone to be connected and dialed? How did the engineers know these increased speeds were possible?

The answer lies back in 1948 with Dr. Claude Shannon who wrote a seminal paper, “A Mathematical Theory of Communication”. In that paper he laid the groundwork for Information Theory. Shannon also is recognized for applying Boolean algebra, developed by George Boole, to electrical circuits. Shannon recognized that switches, at that time, and today’s logic circuits followed the rules of Boolean Algebra. This was his Master’s Thesis written in 1937.
Shannon’s Theory of Communications explains how much information you can send through a communications channel at a specified error rate. In summary, the theory says:
- There is a maximum channel capacity, C,
- If the rate of transmission, R, is less than C, information can be transferred at a selected small error probability using smart coding techniques,
- The coding techniques require intelligent encoding techniques with longer blocks of signal data.
What the theory doesn’t provide is information on the smart coding techniques. The theory says you can do it, but not how.
In this article I’m going to describe this work without getting into the mathematics of the derivations. In another article I’ll discuss some of the smart coding techniques used to approach channel capacity. If you can understand the mathematics, here is the first part of the paper as published in the Bell System Technical Journal in July 1948 and the remainder published later that year. To walk though the system used to fit so much information on a twisted copper pair, keep reading.
Information Theory in a Nutshell
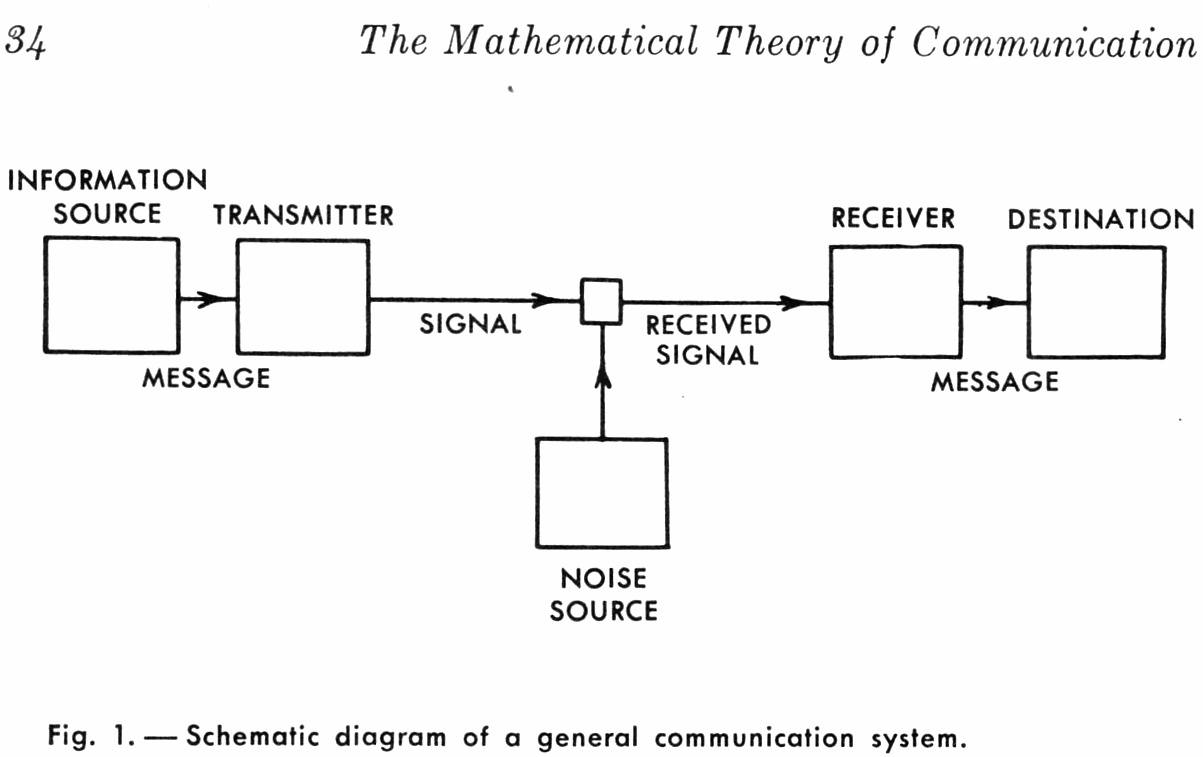 Let’s start with a diagram to understand the basic problem. We have information sent from a source by a transmitter through a channel. The channel is disrupted by a noise source. A receiver accepts the signal plus noise and converts it back into information. Shannon determined the maximum amount of information you can reliably move through the channel. The maximum rate is determined by the bandwidth of the channel and the amount of noise, and only those two values. We can see intuitively that bandwidth and noise would be limiting factors. What’s amazing is that they are the only two factors.
Let’s start with a diagram to understand the basic problem. We have information sent from a source by a transmitter through a channel. The channel is disrupted by a noise source. A receiver accepts the signal plus noise and converts it back into information. Shannon determined the maximum amount of information you can reliably move through the channel. The maximum rate is determined by the bandwidth of the channel and the amount of noise, and only those two values. We can see intuitively that bandwidth and noise would be limiting factors. What’s amazing is that they are the only two factors.
Bandwidth
It is obvious that a channel with more bandwidth will pass more data than a smaller one. The bigger a pipe, the more can be pushed through it. This statement holds true of all communication channels whether radio frequency (RF), fiber optic, or a POTS twisted pair of copper wires.
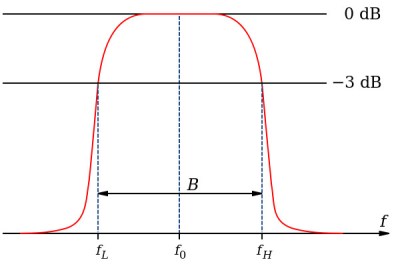 The bandwidth of a channel is the difference between the highest and lowest frequencies that will pass through the channel. For example, a POTS voice channel has a low frequency of 400 Hz and a high frequency of 3400 Hz. This provides a bandwidth of 3000 Hz. (Some references say the low frequency is 300 Hz which provides a 3100 Hz bandwidth.) In reality, channel limits are not sharp cutoffs. Shannon used a 3 decibel drop in signal strength to determine the limits.
The bandwidth of a channel is the difference between the highest and lowest frequencies that will pass through the channel. For example, a POTS voice channel has a low frequency of 400 Hz and a high frequency of 3400 Hz. This provides a bandwidth of 3000 Hz. (Some references say the low frequency is 300 Hz which provides a 3100 Hz bandwidth.) In reality, channel limits are not sharp cutoffs. Shannon used a 3 decibel drop in signal strength to determine the limits.
A twisted pair has a larger bandwidth than 3000 Hz so they are not the reason for the narrow POTS bandwidth. Phone companies impose this limited bandwidth so they can frequency multiplex long distance calls on a single line. The bandwidth limit is acceptable because human speech is intelligible using this band of frequencies.
Nyquist Rate
Shannon’s theory built on the work of Harry Nyquist and Ralph Hartley. Nyquist, analyzing telegraph systems, took the first steps toward determining channel capacity. He determined that the maximum pulse rate of a channel (PDF) is twice the bandwidth. This is the Nyquist Rate (if you beg to differ, please see my note at end of article about ‘Nyquist’ terminology). In our 3000 Hz POTS channel we can transmit 6000 pulses per second, which is totally counterintuitive.
Let’s send a 3000 hz sine wave signal through the channel. We somehow chop off all the negative lobes of the sine wave. If we designate the remaining lobes as 0s and the missing lobes as 1s we are sending 6000 bits through the channel. Nyquist discussed pulses but we would now call them symbols in communications work. The number of symbols per second is a baud, named after Émile Baudot who created one of the first digital codes. It is incorrect to say “baud rate”, since by definition it is a rate.
The formula for the Nyquist Rate is:
C is the channel capacity in symbols per second, or baud
B is the bandwidth of the channel in hertz
Hartley’s Law
Hartley’s contribution extended this to use more than two signal levels, or multilevel encoding. He recognized that the receiver determined the number of levels that could be detected, independent of all other factors. In our example of the POTS channel, you might use the amplitude of the sine wave to determine multiple levels. With 4 different levels we can send two bits for every symbol. With multilevel encoding the bit rate for a noiseless channel is given by:
C is the channel capacity in bits per second
B is the bandwidth of the channel in hertz
M is the number of levels.
Noise
It is obvious that noise is going to limit the amount of data that can be passed. This is analogous to the rough inner surface of a pipe causing friction and slowing the passage of material. The more noise, the slower the error-free data rate. Here’s Shannon’s formula:
C is the channel capacity in bits per second (bps)
B is the bandwidth of the channel in hertz
S is the average received signal power over the bandwidth
N is the average noise or interference power over the bandwidth
S/N is the signal-to-noise ratio (SNR)
Shannon’s result is in bits because he defined ‘information’ using bits. Consider a deck of 52 playing cards with 4 suits and 13 cards in each suit. It takes 2 bits (00b to 11b) to represent the four suits and 4 bits (0000b to 1101b) to represent the cards. In total, it takes 6 bits to represent a deck of cards.
A deck has more data that could be transmitted: color as 1 bit, face card or number card as 1 bit, face card gender as 1 bit, etc. These are redundant since complete information is already available in 6 bits. Based on Shannon’s work this is not information any more than telling someone there were new articles on Hackaday. There are always new articles so that’s not information. Reporting a day without articles? That’s information.
The probability that a bit is received correctly or incorrectly is determined by the Signal to Noise ratio. A higher noise level means fewer error free bit transfers. This relates directly to Hartley’s recognition that the bit rate is determined by the ability of the receiver to correctly detect the multiple signal levels. Errors start to occur when the noise level exceeds the receiver’s ability to differentiate good and bad symbols. The impact of noise on a symbol may actually depend on the specific symbol. Low-level amplitude modulated signals can be overwhelmed by the noise while symbols of higher amplitude are okay. Other modulation methods are impacted by noise in other ways.
The Phone Company Cheats
Earlier I asked how DSL works through the same line that handled your Grandmother’s phone. The basic answer is the phone companies cheat. Seriously, the line from your house to the first phone company location is unfiltered allowing DSL to use the full bandwidth of the twisted pair. At the phone company end they split the voice and DSL signals. The voice is limited to the 3000 Hz and the DSL left at its full bandwidth. That little filter you have at your house is a bandpass filter to block the DSL signals from your handset.
I mentioned that Shannon’s theory doesn’t answer the question of how to achieve high throughput. In the next article we’ll look at some of these techniques, which include error detection and correction on a noisy channel.
A Comment on Nyquist Terms
There is conflict among references on the meaning of Nyquist Rate versus Limit or Sampling Theorem. The confusion highlights how much Nyquist contributed since if the amount were less there’d be no confusion. A Wikipedia article might not be definitive but the one provided for Nyquist Rate explains the two conflicting meanings of the term.
















If your old enough, and had even a passing interest in telecommunications and electronics back in the Sixties and were told that one day that real time video would be carried on twisted pairs to your home you would have snorted in derision. Even now, though I understand how it is done, it still strikes me as a minor miracle.
In the late 50s early 60s a friend of mine leased a line from BT (UK) and used it to transmit video baseband over 4 miles. It ran like that for several years, until BT put the 3.4k bandwidth limit on.
Back then that line would have been leased from the Post Office!!!
Even though this all looks very straightforward, I could never understand why you can’t make phonecalls with a modem. I mean, modems have the hardware required to transmit analog in those frequencies, why not straight speech?\
some could. They were called voicemodems.
Some of the later modems did that, you got a speech channel + 14.4K data. If you mean using a modem just to send audio down, later modems also offered answering machine functionality with software on the host PC. So you could.
https://en.wikipedia.org/wiki/Voice_modem_command_set
Here y’go.
There are several ways this is done. Look at the block diagrams for parts from Conexant and Silicon Labs Voice DAA’s and modems.
The parts exist but they are relatively expensive — demand is a lot lower than it used to be for voice. The systems have to handle handset echo cancellation, line echo cancellation and a variety of other analog functions, in real time. This is typically done with a DSP.
Data modems are cheap because they don’t need all of that other DSP work.
Speaking of “baud rate”, I feel the same way with the term “rate of speed”… speed is, in itself, a definition of the rate of travel from point A to point B. Speed doesn’t cyclically happen over and over again, giving it a “rate” or frequency. It has always bothered me.
Rate of speed is acceleration.
A much more misused unit is kilowatts-per-hour (kW/h), which is technically the output ramping rate of power stations, only expressed in an unusual magnitude. Normally it’s something like megawatts per minute.
Rate of (change in) speed is acceleration – delta v
‘Rate of speed’ is a nonsense phrase.
kW/hr is just a unit per time – either as a usage or a ramp – it defines the change, it can be used in a lot of ways and the main one – average power used over time, is as correct as the use as the ‘pseudo unit’ for generator ramp capability – rate of change of output
kW/h actually parses to J/s^2 in SI units, which describes accelerating energy consumption over time. It cannot be “usage” or average power over time. It simply doesn’t work that way, which is the point.
In a similiar fashion, “rate” itself implies change in a unit without explicitly adding the word, so “rate of speed” actually means acceleration. What isn’t implicitly specified is whether the acceleration is relative to time or space, or something else.
A rate of speed could be the change in speed along a path, where you are interested in for example knowing at what rate the speed of a car changes when it goes around a tightening corner.
“kW/h actually parses to J/s^2. ”
But you are probably referring to kWh, the common scale used for electric bills, not kW/h.
its (j/s)*s not j/(s*s).
Only “small” power stations can afford several megawatts per minute, the rest have to take their time, otherwise they’d thermally shock the system ;-)
Watts per second is another redundancy. 1 watt = 1 watt/second. Any higher amount like kilowatt, same deal. No need ever to mention seconds with watts. Other units of time, yes.
huh? That’s kind of a nonsense cyclical definition.
Isn’t a watt is a joule/second?
It is.
People just don’t understand Watts – they think it’s like miles or hours – something that accumulates.
That’s why there should be a metric convenience unit similiar to the BTU. Something larger than a Joule, preferably equal to one kWh but without a watt or a hour in the name, so as to not create the confusion.
Megajoule comes close, but it’s the wrong size to be useful.
what exactly would be wrong with megajoule, gigajoule, terrajoule ? if people can use the prefixes for bragging about their electronics, surely they can use the prefixes for meting out energy?
A BTU is a kilojoule, close enough (1.055 kJ). A MJ is to a kWh as a foot is to a meter, close enough. If you think that one but not both of feet and meters is the wrong size to be useful, you have a pretty fine notion of utility.
@[ludwig]
As the cost of energy goes up due to global warming then perhaps the unit for energy usage should be “Gold Pressed Latinum”.
Its the typical conflation of quantities with units. If we denote units as [quantity]:
[mass]=kg (kilogram)
[charge]=C (coulomb)
[symbol rate] = Bd (baud)
[data] = b (bits)
[information] = b (bits again)
[bit error rate] = bps
So “baud rate” sounds as stupid as “bps error rate”
There is no conflation.
Baud has an entirely different meaning to bps. You even mentioned it as “symbol rate”.
Bytes per second may seem the same but it doesn’t accurately describe the protocol.
A typical baud rate of 9600 8,n,1 is running at 86400 bps and if you divide that by 8 you get 10,800 and not 9,600
And what about when the stop bit is one *and a half* times the length of the other bits. How do you go from that to bps?
My grandma’s phone, at least, can’t just be plugged in and used–it doesn’t have RJ11, or *any* jack for that matter, and we’re pretty sure it can’t be used to dial out even if it does get connected somehow.
my grandma keeps her phone in her bra, weirdest thing I’ve seen. talking to grandma’ then her shirt randomly starts ringing.
I bet it can. Pulse dial still works in most locations and the audio specs haven’t changed much. Also, those old phones were built to last.
Switchhook dialing..
http://www.oldskoolphreak.com/tfiles/phreak/sh_dial.txt
Yeah I used to do that as a kid, I could order a pizza without ever touching the dial.
I hadn’t done that since college (I’m 53) but demonstrated it to a youngster (30ish) and made his phone ring on my first attempt in over 30 years.
Yup. My grandparents across the road have an old rotary phone that does have RJ11, and it is plugged in and working. I’ve made calls with it. This is Durham, Kansas, serviced by CenturyLink.
If you’re in the US, that phone dates to when everyone rented their phone from the Bell System; you weren’t allowed to connect just any phone to the network yourself. However, with a bit of rewiring and a pulse-to-tone converter, that phone could be used just about anywhere, as long as the ring voltage (at least 60V) and loop current are sufficient. The office switch probably still accepts pulse dialing.
If you are talking rotary phone, it should still work. I have one that runs through an adapter. Search “4-Prong Modular Adapter”
It’s ran through one of those, doesn’t work to dial out though (think something with the dial is wrong).
Try and reversing the wires (tip and ring). An old technique to verify polarity was to wire up the phone and if you can “break dialtone” by dialing via pulse or tone(dtmf) then the polarity is correct. If you’re unable to break dialtone the polarity would often be reversed. Roll em if ya got em!
I’m pretty sure the bits responsible for the dial working at all are broken, and I can’t open it up to find out because it’s a sealed fancy marble box.
Filtering is cheating? Really? What are they cheating us out of?
Also, DSL-alike tech has been around for decades, it’s only when people started wanting a home pornography feed as the internet took off that anyone bothered selling it to home subscribers.
I thought the upgrade to DSL speeds was made possible by building more DSL hubs nearer to homes… You can’t really run DSL on the same infrastructure that used to be there before, all the way back to the Telco office and onto the net. Now POTS goes down the block to something that can actually reach those speeds.
That’s the “cheating” bit. DLS only works for a couple miles. That’s also where the article is wrong. The DSL signal only goes to the nearest repeater which is most likely buried in an utility well or box down the end of your street. From there on it’s converted to coaxial or fiber.
They’ve long since pulled the twisted pairs off the poles, or left the underground pairs dark.
Okay, my statement “first phone company location” wasn’t clear. I was trying to convey something like, “as soon as they can”. I almost said “first point of presence” but wasn’t sure that was correct, either.
Around here, it’s the meth addicts that pulled the twisted pairs off the poles…
That’s the DSLAM. Digital Subscriber Line Access Module. Expanding the reach of DSL involves installing expensive DSLAMs dotted around the countryside. If the telco doesn’t figure enough people in your neighborhood are going to subscribe to DSL, then you are SOL.
Some telcos will even refuse to install a DSLAM if you round up enough of your neighbors to say they absolutely will get DSL if it was available.
They can be kinda dense that way, like grocery store managers who refuse to stock a product that there’s definitely a demand for, then say they don’t stock it because “it doesn’t sell”. You cannot sell what you refuse to make available. My favorite examples of this dumbness are Strawberry Shasta and DAD’s Orange Cream. I’m pretty sure Shasta stopped making strawberry for a long time (latest post on their Facebook shows a pic with cans of strawberry, black cherry and ‘red pop’ so perhaps a comeback), replacing it with (ick) kiwi strawberry. Around here, some stores will order in a pallet or two of various DAD’s flavors and I gotta be fast because it’ll sell out pronto – yet despite the extremely obvious demand the stores refuse to make the brand a regular inventory item.
The reason is self-competition. They product they refuse to stock would displace some other product with a better profit margin. They don’t want you to buy the better product, they want you to buy the product they make more money out of, such as crappy shop-brand ice-cream instead of Ben & Jerry’s.
Same thing with DSL. Telcos are often charging an arm and a leg for dialup access in fringe areas, by the minute no less, and because dialup is slow people end up racking minutes and paying hundreds of dollars a month for internet access. The DSL would cost the customers considerably less per month, and the DSLAM costs money, so even increasing the number of customers in the area would put the company profits down.
DSLAMs cost a surprising amount of money to install.
Electricity connections often cost $10k+ depending on the utility (the DSLAM needs power). Fibre can cost in the region of $50k/mile (the DSLAM needs to connect you to the internet). Then you need all the equipment in the box, the box itself and a place to put it.
IMO if you don’t even have DSL it would be a great chance to setup a community WISP or even a community Fibre Co-op like B4RN.
B4RN has like 95%+ uptake rates (which is insanely high, a gigabit provider in a town might only plan for 30-50%), because there’s barely an alternative. As soon as people have reliable 5+ mbps ADSL even gigabit becomes a much harder sell – yes 30-50% will jump right on board, but that’s half the revenue on the same costs.
My grandma’s phone did not have a dial. You picked it up and asked the operator to dial for you….
Switchhook dialing..
http://www.oldskoolphreak.com/tfiles/phreak/sh_dial.txt
can’t wait for coding tecniques part.. well done, author :)
DSLAMs are just cool sounding
Back in the late 90’s, I did an avionics project at the Salt Lake City airport that used the airport’s “private” POTS lines. This sent a copy of the ILS localizer’s 90/150Hz control information on a 2600 Hz audio carrier to a remote processor to verify the integrity of the ILS signal transmitted (to guide landing planes). The spec said the line was “unconditioned” (per some Bell standard), 19 ga twisted pair, and no longer than 5000 ft . In reality, it was about 26,000 ft (per reflectometer) of a combination of 19 and most 31 ga twisted pairs with 4 or 5 junctions. When the local phone company was called in to check the line, they provided a bandwidth plot that showed the line did not fully meet spec as it was too attenuated at 3 KHz and had several notches in bandwidth due to the comb filter effect of the various lines and junctions and conduits the lines were in. The extra length also contributed to the larger than expected copper loses, especially with temperature changes (which would not have been so large if the conduit was really below the frost line). That explained why my code “did not work” as expected. So I had to make changes to “fix” my code. Note that often in cases like the civil work at an airport, they run high-voltage, high-current, AC right alongside the “delicate” signal lines like the one referenced here. This would couple any AC noise into the signal lines, and if the twists weren’t perfect (and they never really are), then the “noise” coupled into the lines can be unbalanced and cause signal degradation. This is NOT the nice, well-behaved, classical Gaussian noise used in most communications signal processing treatises. It’s the real deal.
Unconditioned lines, then and now, can have a myriad of issues with them. I wouldn’t be suprised that if you were getting a huge drop at 3KHz there was a load (H88) coil left somewhere along the span. Improperly spaced or unbalanced loaded pairs will cause messy hard to troubleshoot issues too. That was a big issue for us when trying to get ISDN everywhere early in the 2000’s. We would run a nyquist on the line and everything would fall on its face at 3kHz where we required over 8kHz. I still work with those copper spans to the SLC airport. Now we have fiber fed systems to most of SLC international but there is a lot of copper feeding that place. I do work for the local telco.
The details of HOW DSL works are very interesting. It’s a lot more than just sending data down the line. Multiple carriers, and the number of bits assigned to each carrier are allocated (and periodically re-allocated) using the bit error rate (BER) for the carrier. Higher BER, fewer bits assigned to that carrier.
Orthogonal Frequency Division Multiplexing.- OFDM
Especially interesting (and impressive) is how Vectored VDSL works. It allows me to get 100 Mbps over the same old copper wires that were buried when the first analog phones appeared (the lines are a bit shorter today, of course, but still about 1/3 mile)
There’s DSL and VDSL. Original DSL ran on your twisted pair from your location to the “Central Office” in the town or local area. The farther you were from the CO the slower your maximum data rate would be. VDSL as used by AT&T Uverse runs on the old copper between the house and a neighborhood box, then fiber. Speeds are still limited; at least in my area the maximum available is allegedly 12 megabit (I pay for 6 and usually get 3-4, so would I get at least 6 if I paid for 12?). Yes, I’ve heard of Uverse-type services providing higher rates, but I wonder about it if the neighborhood lines aren’t brand new; when it rains hard, for instance, even though everything’s underground I still get speed drops into the 1-1.5 range at times. The phone co. isn’t going to change out those neighborhood lines anytime soon, if ever. Frankly, I’m looking at cable even though I don’t need TV because even their cheapest Internet service (comparable in price to mine) is 10 megabit. Bigger pipe…
Here in Australia most people are still on conventional ADSL2+. I am currently syncing (per my router) at 9215kbps down and 984kbps up and unlike many Americans I get a choice of many different ISPs (quite a number of who run their own DSLAMs in the local phone exchange).
I do pitty the people here in Australia that are stuck with crappy service (including all the people stuck in “RIM port hell”) but that’s why I made sure the apartment I am renting had good options for ADSL before I even applied for it.
Quote: “My DSL line downloads at 6 megabits per second”
As soon as I read that I checked mine.
I have 16.822Gbps down stream (yes Gb) and 1.087Gbps upstream.
Surely you mean 6 Gigabits per second
No, megabits, and I just checked it again. I went to speedtest.net and ran the test just now. The meter is scaled up to 100Mbps.
Mine’s the same.
What network setup are you using to even get over 16Gbps into your PC? Even among high end PC hobbyists, faster than 1Gbps LAN hardware is rarely used at home.
The short answer is that I don’t get any high speed to my PC (currently a laptop).
I used to do server maintenance / web development / zone management / database management / backups for a internet business and backups / database transfers were too slow from here so they installed a NTU which has four ports. I used to use four cables that go from the NTU into a special card in the desktop PC right up the front of the building. I don’t own the building so we couldn’t make the cables permanent.
Anyway even though I still do work for them from time to time … I don’t need any speed for what I do for them now.
The PC up the front is really really fast (they gave it to me for work) I only use it for VHDL synthesis now as the other PCs/laptops are much slower.
Here’s the thing lol. I am now at the back of the building so I can only use WiFi. There is a G+ router plugged into the NTU, nothing else is plugged into the NTU anymore.
The WiFi router is max 108Mb/s but because I have ‘n’ WiFi at the back of the building I can only get 54Mbps. The old hardware (computers) were also G+ (108Mbps).
The figures I mentioned before are from the NTU’s management interface and I don’t know if they are the actual speeds to the NTU from the exchange or just the speeds that it is capable of because by the time it gets down here it’s under 50Mbps because of the WiFi bottleneck. The exchange is a very short walk from here.
VDSL2 has a maximum theoretical speed of 250 Mbps. No way you get 16 Gbps over DSL. Over optic fiber, maybe.
Oops. Convert mega->giga. Brain fart. It’s still pretty slow compared to what most people here seem to have, but it’s what I can afford and the best available (non-cable) isn’t much better. Yes, it’s in the U.S.
Oops again. I did remember correctly – it’s megabits. Just checked AT&T’s web site. Maximum speed available now (advertised, anyway) is 18 mbps. FCC’s definition of “broadband” is now 25 mbps. Gigabit is what Google provides, and requires fiber to the house.
.. In the next article we’ll look at some of these techniques, which include error detection and correction on a noisy channel. Please notify my when it appears
I could accept the DSL numbers because the signal is intercepted by the phone company, bypassing the 3000hz pass-band limit. But I vaguely remember hooking up a 56K modem without subscribing to anything. So doing the Hartley Law math, the number of received levels would have to be 645 (56,000 = 2 * 3000 * Log2(645)). Being able to discern this many levels using phase (let’s say 26), and amplitude (also 26, so product >645), for two modems spanning a continent seemed either magic or sales specs. And this law is over noiseless channel! Of course I never remember actually receiving anywhere near this rate, so the 56K number didn’t mean much to me. Does anyone remember actual phase and amplitude levels for the 56K boxes?
I can’t wait for the next article!
At the time that 56k modems were popular, the voice lines were already implemented as 64kbps digital signals (8 bit * 8 kHz). The 56kbps was only achieved from ISP to subscriber, because the ISP could cooperate with the central exchange to have their signals transmitted digitally for most of the way. Only the last part was analog, using appropriate filters for minimal signal loss.
Yup. They could’ve made 64k, but apparently the maximum signal level was limited, for safety I think.
What I read is that some of the bits were used for signalling purposes.
https://en.wikipedia.org/wiki/Channel-associated_signaling
You *mostly* got it.
To run a synchronous signal over an asynchronous carrier you have to run at a rate less than a the full speed for you will loose sync from end to end.
The digital equivalent is sampling –
If you have an incoming bit rate of 1000 bits per second and you sample at 1001 bits per second then you can reproduce the signal at the other end, and one bit in every thousand will be sampled twice.
On the other hand – if you have an incoming bit rate of 1000 bits per second and a sampling rate of 999 bits per second then on in every thousand bits will be lost beacuse it was never sampled.
The only way to get 1000 bits per second through a 1000 bits per second carrier is to synchronize the sampling with the incoming bit stream. This doesn’t happen with modems as the carrier (POTS) is asynchronous.
You also need so overhead to cope with system variations.
@RÖB: not quite. You can have a sampling rate of 1000 bits per second and a incoming stream of 1000 bits per second, and still achieve time synchronisation. All it requires is that the signal to noise ratio is somewhat better than strictly needed for the signal. For example, assume QAM + OFDM modulation. A small timing error can be detected by a rotation of the QAM constellation, and subsequently corrected for the next symbol. As long as the noise margin is good enough to properly disambiguate the incoming bits, and the timing error is small, this doesn’t result in bit errors.
Ok Artenz let me get a handle on this …
you can reproduce a 1kbps stream by sampling it asynchronously at 999bps?
I mean reproduce it perfectly – nothing lost – like going from a synchronous data stream to an asynchronous carrier doesn’t matter.
There is a problem with your theory about error correction and that is exactly why there is this lee-way.
There is a cost to correcting errors and often (well always without exception) it is far greater than the load of the original data. When you go to far and get to a point that you *need* significant error correction then the cost is so heavy that it outweighs the benefits of going so far in the first place.
Real World Translation – if you try to push a 64kbps synchronous signal through a 64kbps asynchronous carrier then at the first data error – which is inevitable – your throughput is going to come cascading down to 32kbps because you will spend just as much time correcting the cascading errors as sending data.
This has been proven with nyquist theorem. And not the bandwidth = half the sample rate stuff, there is more to nyquist theorem than that.
Just guessing but increasing the signal level might cause cross-talk with other wires.
It is not “Hartley’s Law”, it is “Shannon’s Theorem”. At the time Shannon presented the most complete treatment of the Noisy Channel Coding Theorem in 1948. Shannon’s work was based in large-part on previous and concurrent work by Harry Nyquist and Ralph Hartley.
A subject like this, even at the introductory level, really shouldn’t stand without at-least a cursory treatment of inter-symbol interference and the role of matched filtering in mitigation.
A writer can only cover so much in an article like this. It’s possible I will do a article that addresses the ‘wire protocol’ issues which would include Nyquist’s work on inter-symbol interference. But if I get to that article I’ll need to decide if readers would rather hear about ISI or, say, OFDM.
BTW, I didn’t say it was Hartley’s Law. I know the headings we use aren’t always clear but the Noise is a Heading 1. I presented Shannon’s formula there. Here again, there is a nomenclature issue is it Shannon or Shannon / Hartley. Or even one of 4 or 5 others who came to similar conclusions even before Shannon?
A 56K modem has a download speed of 57.6Kbps, not 56.6K.
If you’re going to complain about inaccuracies, at least get it right. 56k didn’t exist; it was limited to 53.3kbit/s because of FCC power limits.
Presumably it could be 56k elsewhere in the world, as I’ve seen it called out as 53k due to US regulations, but never explicitly seen an example of where it worked at 56k.
It worked at 57.x kbps in Australia but that is probably because or channel bandwidth is a little wider. I think it was 300Hz to 3.4kHz from memory.
That’s interesting, that it could go beyond the 56K. The 56K limit was set to limit power output, a legal requirement, hobbling the modem’s natural limit of 64K. Even if Australia had wider power limits, it’d mean they’d have to put separate firmware into the Aussie version. At least into the line cards at the exchange. I suppose if they did, maybe the modems were programmed to accept that.
Or is it just a case of unit conversion error? In old-fashioned text modes, you used start / stop bits, so every 8 bits of data took (say) 10 bits to transmit. In block data mode, the mode you’d use for PPP / Internet, you got 8 bits of every 8. Mostly. Might be the software that gave you that figure was a bit off, somewhere. The modem itself would report connection speed, when it achieved a connection, depending on your dialup software you might be able to see that string.
It’s a close figure, so it might be there’s some error somewhere. If they really could do faster than 56K, I’m surprised. Never heard of it before.
The bandwidth btw would be a full 8K samples per second, equivalent to 0 – 4KHz, not 300 – 3,400Hz. With a limit like that, you’d only get 49K, all other things being equal (and they wouldn’t be!).
The 56k modem is confusing for a couple of reasons. There were 2 incompatible vendor versions originally. The V.90 standard combined them in a way that allowed existing units to be reflashed to the new standard. That was supposed to be the last standard but it was replaced by V.92. A lot of the speed gain over 33.6k was through the use of real-time compression in the modems. If you downloaded a zip file you wouldn’t see 56k. ISPs also needed to use a digital connection to the telco. They were a kludge on a kludge that worked enough times for people to be happy.
Nope, 56K wasn’t done with compression. It grew from monopoly-busting of phone companies, in lots of countries. That meant ISPs could put cards in phone exchanges. The ISP’s own connection would be a single high-bandwidth digital connection, connected to the cards. The cards had access to the phone line, allowing 8KHz bandwidth with 8 bits of resolution. 8Kx8=64Kbps.
The 56K was, as mentioned, because of power limits at the upper level of the signal range. Modems usually had 12-bit ADCs to be able to make sense of the 8-bit modulation plus noise that they’d receive.
Modems did also offer compression of course, I think even 9600bps ones had that, one of the V-number standards. But the dialup Internet was designed strongly around the data rate limitation of modems, so websites used GIF and JPEG compression, which wouldn’t compress much more that they already were. Text had an advantage, was fairly well compressible, so that’s one thing modem compression could help with.
If you downloaded a compressible file over a 56K line, you could get faster than 56Kbps. An external modem would often connect to the host PC at 115,200. Internal modems technically didn’t have a host connection speed limit. 56K was a reference to the phone-line data rate, not counting added compression.
Yup, there were 2 standards, US Robotics with “X2” vs Rockwell with “K56Flex”. It ended up K56Flex became the standard for everyone except USR. But in the end the ITU-T settled on a compromise between the two. Since 56K modems were designed with this happening in mind, they pretty much all used a DSP and flash ROM, so a simple download to the modem upgraded the software and made them all run V90. Then V92, which was a teeny bit better.
It wasn’t a kludge, it was a benefit from phone exchanges going digital all the way to the line cards. A genuine technical development, different from 28.8K, which was previously thought to be the absolute limit for POTS modem speeds. And 33.6K was a tweak to that.
Re de-monopolising, in the UK many ISPs registered themselves as telcos. It was thought at the time this was so they’d be entitled to a share of the per-minute call charges everyone in the UK paid back then (yes! even for local calls!). Internet used to cost a damn fortune back then. You needed offline readers for Usenet and email. Registering as telcos got them money for every call they carried, even though those calls were all to the ISP itself. For a while we had Freeserve, who had no monthly fee, their income came solely from this half-penny per minute they got from the calls. The economics happened to work that way, at that time. Before that, you’d pay around a tenner a month to your ISP, and your per-minute call costs all went to your phone company.
One or two ISPs, back then, tried starting 0800 services, actual free calls. In this case the ISP paid for the call, no small amount of money. Dunno how that was supposed to work. In the end, it didn’t! I also remember thinking “that’ll never work” when Youtube started. All that bandwidth! Video! For free! Bankrupt in a month!
In the end, throwing away a load of money to get in there first, well, as we know, they did quite well out of it.
Without limits, they’d be 64K modems. The limits limited it to 56K, in the UK and some other countries at least. Imperfect lines could limit it to below that. Depended on what line you got, each time you called out, and probably the weather and the chief engineer’s zodiac sign / blood pressure.
Mine would report somewhere from 43K – 53K most times. I think I got 56K now and then. In the UK. No idea how old my phone line was.
If American modems were stuck at 53K, that’s just the FCC being more conservative over signal limits than other countries. The tech definitely allowed for 56K. Blame the FCC, not the modem manufacturers.