 Nitinol is a kind of wire that has a memory. If you heat it, it tries to return to the shape it remembers. [Latheman666] recently posted a video (see below) of a Nitinol engine that uses a temperature differential to generate motion.
Nitinol is a kind of wire that has a memory. If you heat it, it tries to return to the shape it remembers. [Latheman666] recently posted a video (see below) of a Nitinol engine that uses a temperature differential to generate motion.
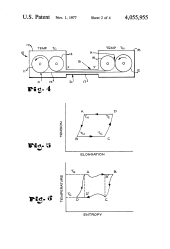
[Dr. Alfred Johnson] holds a patent on this kind of motor. The concept sounds simple enough. A Nitnol spring shrinks in hot water and expands in cold. The spring is looped over two pulleys. One pulley is geared so it has mechanical advantage over the other one so that there’s a net torque which moves the hot part of the spring towards the cold side, and feeds more cold spring into the hot water. The cold spring then contracts and the entire process starts again.
We haven’t entirely gotten our heads around the gearing, but it seems plausible. On the other hand, this video was posted on April 1. What say you, Hackaday Commenteers?
If you are expecting a slow, low-energy motion, watch the video and you may be surprised at the activity. We’ve talked about wire-based motion before, but it was a little more leisurely. Then there are always jumping robots.
Thanks for the tip [Keith O].















That’s definitely feasible but it takes a energy to make ice on one side and heat the water on the other, so an electric engine is going to be a lot more efficient.
you could run a radiator and fan to remove heat from the cool side, and build a fire on the hot side, and run on literally any fuel source available (even solar!) I wonder how big it would have to be to run a cooling system and still have power to spare(If it’s even possible).
You are right… but wrong too. It’s value is probably mostly as a curiosity, or a demonstrator of the science involved. A toy to get people interested in science maybe.
But.. if I was going to try to make something like this into a viable tool that does some sort of serious work it would be somewhere that nature provides the heat differential. I wouldn’t heat and cool water myself! For example.. maybe a really long version could be used vertically inside a lake or ocean where the water is naturally hotter and colder at different depths. Or.. maybe somwehere that the climate is normally cold but geothermal energy is easily accessable like greenland you could rig up a container that is constantly getting resupplied by a hot spring and a second container that is not.
Maybe such things could provide enough power to run environmental sensors or something like that where replacing batteries is inconvenient, utility lines are unavailable and sunlight is insufficient.
A Stirling engine already does this trick and I bet more efficiently. No use for this now but maybe someone will find a use.
Power density is another factor that determines which solution is more viable for a given application.
Much more efficiently.
Nitinol wire contracts because of the re-organization of its crystal matrix. It has a hysteresis of about 15 C to transition from one crystalline phase to another, and because the material has a fairly high specific capacity of heat, it takes considerable amount of energy to raise the temperature – heat which gets dumped in the ice water.
As a result, practical nitinol motors have an efficiency around 2-5%
For better results, you need a heat activated material which has low mass, low heat capacity, low thermal conductivity and doesn’t need to swing over a huge temperature difference for a change in pressure or shape. That’s describing the properties of air and hydrogen in a stirling engine.
An electric motor requires prime mover if heat is to be converted to work, so it depends on the circumstance (form of energy available)
Wow! Yeah, I fully admit that I was expecting a “generates several nanowatts, enough to power a sensor reading every few months” sort of motor before watching the video.
What’s the word on durability, though? Is there a shape memory analogue of metal fatigue to worry about?
NiTi alloys do pretty well for metal fatigue as they shift crystal structure when they go through temperature transitions and that helps fix the lattice dislocations that typically pile up to cause fractures.
Doesn’t mean it’s not nanowatts. It can idle pretty fast, but no idea what kind of torque it can pull.
And it winds down in a hurry. Looks like the motor induces considerable mixing in the liquids. I have a hard time imagining a situation when this would be a good motor.
How about lightweight hexapods?
I suppose you could cover the springs in some kind of water-repellent. In itself it’s probably not suitable for much, but it’s an interesting principle.
The coiled wires pull the water along and that makes it into a water pump. You can do the same motor with straight wire as well, but it needs multiple loops.
As for the torque, it can produce absolutely massive amounts of torque – likely enough to pull itself apart in a straight-wire configuration.
This same thing was done wayyyyyy back in the early times after the invention of Nitinol. I want to say 20th century but not exactly sure when.
20th absolutley, I’ve seen demos of this before, though not as a spring I think
The patent that it’s based on is 1976. So yeah. It’s not new, it’s just freaky.
I’ve definitely seen, held, touched one in person and observed its operation. My high school physics teacher had one as a demonstration in 1994 (I am old.)
Thanks a lot! ;(. I was in highschool in 1994 too.
I’ve definitely seen, held, and confirmed the operation of one of these in person. My high School Physics teacher had one as a demonstration in 1994. (I’m old.)
Connect the motor to a load. Does it still spin?
Also, it seems like this might be usable to pump water, if the Nitinol belt had some cup-shaped “buckets” on it.
Yes, and yes, in fact that was one of the early proposed applications as just the heat gradient between the ambient air and ground water could drive the engine so that the water it pumped for irrigation also powered it.
Checkout this old video about the work done with it at Mcdonnell Douglas.
https://www.youtube.com/watch?v=8-dCIkJAjyM
it would also have the side effect of pumping more water during hotter periods, like drought, and less water when the sun doesnt shine….
Hm. The pulleys appear to be the same size, but they’re attached to different-sized gears. Meaning they’ll have different rotational and linear speeds.
So the rubber will wear down, unless there’s some kind of weird effect with the shape memory alloy?
That’s the idea. The spring is more compressed going one way than going the other. Of course the same mass of metal goes each way — otherwise all of the spring would end up on one side!
Ah! So the gear ratio is set based on the expansion / contraction of the spring? So presumably you need different gears depending on what temperatures you’re working with? Or is Nitinol a kind of Scmitt trigger thing, with a threshold?
Try search term “Nitinol hysteresis”
http://memry.com/nitinol-iq/nitinol-fundamentals/transformation-temperatures
The wire contracts while it is on the hot side so it takes less motion to pass the same amount of wire back to the cold side.
Doc Johnson is also the name of a sexy time toy company.
The more you know.
Evidently, Doctors named Johnson have an affinity for elastic materials.
i thought this post was about dildos. moving on…
That brand has decent market penetration.
You win this thread, Inspector Gadget…
Reported
At least you didn’t try telling them to not be a dick.
*cough*
Too obvious, sockpuppet.
Eeeww I really don’t want to know what sort of puppetry you’ve been using your socks for.
Oh, i remember these. They used to sell them in Edmunds Scientific if I remember right, it was part of a nitinol demo kit. Then again it could have been one of the other science suppliers like Frey or Carolina Biological.
More examples here,
https://www.youtube.com/watch?v=3MfTJVAtx6w
Different configuration, but he also gangs them together and runs generators off the engine. A few toy ideas too.
That toy boat! I ssooooo want to make one now! Great video.
We are finding new ways to make things spin, cool. Now lets apply it to creating energy.
I’m waiting for the perpetual motion comments on the youtube video
Haha. YouTube comments are usually terrible. I only read the ones for science videos that are buried away from the usual fluff.
That article not too long ago about making your own springs has some excellent comments in it and some good info.
I just watched this video…
[https://youtube.com/watch?v=MctVY2S6RyE]
Most interesting video I’ve seen in a week.
I want to make a solar cube! Probably won’t work without strong sunlight.
Finally! You heard me! After studying heat reactive alloys, nitinol is Defense studied. YouTube vids show docs on this breaking news in the early 70s.
The nitinol engine class was put to bed because it competed with GMs diesel engines. GM was primary contact holder for all naval engines. GM was in bed with EXXON and Shell.
Bottom line, the Nitinol engine IS 98% efficient, works on big scale, is awesome.
Other studies show heat reactive alloys in this area are extremely interesting. Note: experimental alloy in development that turns heat into DC current.
Such alloys are extremely valuable for their ability to convert hot water into DC current. Secondary motor system back ups or secondary power sources are very exciting for new hybrid motor systems. In application with green house aquaculture, these alloys presented exciting new power sources when used in hot humid environmental situation.
Overall, nitinol has been in use since the 60s, hack a day makers and dreamers need to get their hands on this and play with it. It’s awesome!
lol loony tunes conspiracy theories. 98% efficient, might you clarify that, in a thermodynamic sense?
He got it backwards. 98% of the energy in the device is used to change the temperature of the material and not do any useful work.
I can actually see how this could be useful to reduce water stratification (*where the hot and cold layers of the water seperate in large bodies….).
First video link not working. Embedded video fine.
In theory this should work with the coiled fishing line nylon string also… for those who wish to upscale in the cheapest way…
in theory even with a rubber band
“Proceedings of NITINOL Heat Engines Conference”, 1978 (dtic.mil) is fascinating to peruse if you’re into his sort of thing. http://www.dtic.mil/dtic/tr/fulltext/u2/a108973.pdf
The biggest challenge I have seen with nitinol is developing an efficient design–all designs I have seen suffer from serious losses due to 1) Energy” bleeding from the heat source to the cold sink, 2) Frictional slippage, and 3) Water resistance
However, I have an elegant solution to all these issues…First interweave nitinol wire with carbon fibers to form a composite “cloth”–with the nitinol fibers all running parallel. Next connect the two ends of the cloth to form a “BELT”–with the nitinol forming circular rings. Carbon fiber is an excellent conductor of heat and can withstand very high temperatures. It will transfer the heat to the nitinol on the hot end, and help it dissipate on the cold end.
Next, take your carbon-nitinol belt and stretch it across two textured rollers. These rollers should have either pins or hooks to catch your belt and keep it from slipping. Finally–apply heat to one side and cold to the other. If you use 2mm nitinol wire to create a 1M wide belt, it will contain 480-490 individual wires, allowing you to generate over one TON of TORQUE!
BTW–Something to keep in mind is that the nitinol performs work by straightening, pushing against your roller, and thus pulling itself around. You only need to heat 1/2 of the exposed surface ON THE DRIVING ROLLER. The rest of the wire is already straight, and adding more energy will only make it hard to go around the second roller–REDUCING your efficiency. Also, if you heat the ENTIRE roller, you create a pulling force in BOTH directions, also reducing your efficiency.