Think not of what you see, but what it took to produce what you see
Benoit Mandelbrot
Randomness is all around you…or so you think. Consider the various shapes of the morning clouds, the jagged points of Colorado’s Rocky Mountains, the twists and turns of England’s coastline and the forks of a lightning bolt streaking through a dark, stormy sky. Such irregularity is commonplace throughout our natural world. One can also find similar irregular structures in biology. The branch-like structures in your lungs called Bronchi, for instance, fork out in irregular patterns that eerily mirror the way rivers bifurcate into smaller streams. It turns out that these irregular structures are not as irregular and random as one might think. They’re self-similar, meaning the overall structure remains the same as you zoom in or out.
The mathematics that describes these irregular shapes and patterns would not be fully understood until the 1970s with the advent of the computer. In 1982, a renegade mathematician by the name of Benoit Mandelbrot published a book entitled “The Fractal Geometry of Nature”. It was a revision of his previous work, “Fractals: Form, Chance and Dimension” which was published a few years before. Today, they are regarded as one of the ten most influential scientific essays of the 20th century.
Mandelbrot coined the term “Fractal,” which is derived from the Latin word fractus, which means irregular or broken. He called himself a “fractalist,” and often referred to his work as “the study of roughness.” In this article, we’re going to describe what fractals are and explore areas where fractals are used in modern technology, while saving the more technical aspects for a later article.
Measuring Coastlines With the Koch Curve
Let’s jump right in with a good old fashioned gedankenexperiment. Your job is to measure how long the coastline of England is. Let’s say you start off with a yard stick and you complete your measurement, with the end result being X number of yard sticks. Now let’s try with a 12″ ruler. And then with a 6″ ruler. You will find that the smaller your measurement device gets, the longer your coastline measurement becomes. So how does one measure the length of a coastline accurately?
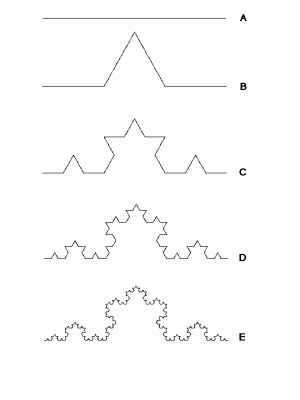
In order to answer that question, we must familiarize ourselves with a fractal technique called the Koch Curve, as seen on the left. Let us imagine an equilateral triangle. Take each side of the triangle and put another little triangle on it. And now take each side of the little triangles and do the same. This iterative process creates what is known as a mathematical “monster,” and is a paradox. The equation produces an infinite and therefore unmeasurable curve. But if you graph out the set of points the equation produces, you find a closed finite shape sometimes called a Koch Snowflake. The image on the left represents one side of our equilateral triangle.
This is in direct relation to our coastline measurement problem. The length of the coastline grows to infinite as we make the measurement device smaller, but there is clearly a closed shape to measure. Mandelbrot recognized this connection, and developed a measurement method that, instead of measuring the length of the coastline, measures the “roughness” of it. To understand this, we need to tweak our understanding of dimension.
A straight line is one dimension. A triangle is two dimensions. If we think of the Koch Curve lying somewhere in between the two, we can see that as we iterate, we increase the roughness. In the image on the left, E is “rougher” than C. And if we think of a coastline like the outer parts of our Koch Curve, we can measure this roughness in terms of the number of iterations of the fractal. This insight would catapult Mandelbrot’s notoriety within the scientific community.
Fractals in Hollywood

In 1978, Loren Carpenter was an engineer for Boeing, and was trying to develop software to make realistic looking mountainous terrain to be used as a backdrop for plane CAD models. He stumbled upon Mandelbrot’s first book in a book store, and read it cover to cover. Twice.
At that point in time, Mandelbrot was not well known, and the term ‘fractal’ was something few had heard of. In the book, Mandelbrot described how many irregular shapes in nature, including mountains, can be thought of as fractals. You can make a fractal by taking a smooth shape, breaking the surface into pieces, arrange those pieces in a self similar pattern, and repeating…similar to how we made the Koch Curve. Carpenter had found his solution.
Within 72 hours after discovering fractals, he had produced mountainous terrain on his computer. He made a rough terrain out of a handful of large triangles. He then wrote the code to break each one into 4 individual triangles. And then, through a process called iteration, repeated this dividing process many thousands of times. The end result of this relatively simple process was a realistic looking mountainous terrain.
Carpenter would go on to work with Lucasfilm and become a co-founder of Pixar Animation Studios.
Fractals in your Cell Phone

Many of us hackers are all too familiar with needing different antennas for different RF frequencies. Your cell phone has a handful of RF devices: WiFi, Bluetooth and a cellular transceiver to name a few. Most phones do not have individual antenna for each radio. The single antenna in your cell phone is what is known as a Sierpinski Carpet fractal. It turns out this style of antenna is the most efficient way of receiving signals for differing frequency bands, and works for all radios in the device.
I hope you enjoyed our little tour of fractals. There are many more examples of fractals in our everyday lives, of course. Let us know of any you’ve run across in the comments below.
Sources
Main Image – Fractal Science Kit
Thumbnail Image – Wikimedia Commons
















One of my favorite videos is The Secret Life of Chaos by the BBC. In the past I was only able to find it on Daily Motion since it was pulled from YouTube for copyright issues. Still up here: http://www.dailymotion.com/video/xv1j0n_the-secret-life-of-chaos-2010_shortfilms definitely worth a watch before it disappears again – especially if you don’t have access to BBC4 which I think was the channel it was re-shown every so often. Amazing video. Wish I could buy it on DVD for showing here in the US.
Maybe this short introduction to a fractal perspective on cosmology fits well here: https://www.youtube.com/watch?v=tN_eNQFcv5E
Also the attached fractalogy.org site is quite an interesting source..
nice one.
One could also mention Lindenmayer Systems, aka L-Systems, which are heavily used to render plants in 3D graphics
The beauty of fractal geometry is worthy of a religion imo.
In a world where geometry goes mad, a renegade mathematician, wrongly accused of squaring the circle, joins forces with a by-the-book cop in a race against global conspirators to clear his name and save his life. And possibly save the Universe!
And I absolutely read that in Don Lafontaine’s voice, complete with hammering drums and the odd background explosion!
Had to g**gle Don but still missing springer’s original reference – ? among us?
Edwin Abbott’s Flatland I believe?
Close but no cigar – https://en.wikipedia.org/wiki/Flatland no reference to “by the book cop” but now I will have to read the whole book anyway, thanks for the tangent!
Just that “squaring the circle” was a goal for mathematicians for ages and was proven impossible when pi was proven to be transcendental in the late 1800’s. So, heretical mathematical crime :-)
Does anyone have an example of a fractal antenna being used in a modern cell phone? I have taken apart a lot of phone and almost always have just little bent lumps of metal for the antennas (and possibly a chip antenna for the gps or 2.4ghz radios)
Yeah, if I had a nickle for every time I saw that one damn stock photo of a fractal antenna. The amateur who developed it patented it, stripped his entire presence from the Internet, and I’ve never seen or heard anything new of it again.
Yeah. I’ve yet to see one in any phone or any other device for that matter. As you said, it is just a little strips of metal on the PCB or a thin flex foil antenna stuck to the case. If the fractal antenna was that amazing then I’d expect all the phone manufacturers to have jumped on board already. Apple definitely would have since they’ve got no problem with throwing money at a new technology if it gets them a thinner/smaller phone but I’ve yet to see one in an iFixit teardown.
Would it help anyway? Phones only use a few frequencies. 850/900 1800/1900, and 2.4GHz for the short range stuff.
There was a (now out-of-print) book called Chaos and Fractals which had a bunch of concise Basic code examples for various fractal algorithms. The code was pretty understandable and fun to play with the parameters to see how it affects the generated images.
I got the book from the library and re-coded all the examples in javascript and put them on my blog: http://sharpk60.blogspot.com/2015/11/re-writing-example-code-from-chaos-and.html
Amazon has new copies, so it must have been reprinted. BYTE and Scientific American used to run articles on most of the subjects and we used to play with them quite a bit once upon a time.
The real question is “what is as dead-easy to use as BASIC was, in order to squeeze a simple graphics picture out of an algorithm?” MATLAB? If memory serves I was doing the Mandlebrot set with thirty or forty lines of code on an Amiga.
I remember being stunned by a Mandelbrot set generator on the Archimedes in 1988, as it only took about 3sec to do 640x256x8bpp. Really showed the power of the ARM vs contemporaries.
I wrote one on the Archimedes! In fixed-point ARM assembly. The first version had a mathematical bug which caused it to show even weirder looking fractals than the standard Mandelbrot set. I wonder if and how fast the code would run on my iPhone… ????
I believe the new copies are of the 2nd edition. Unfortunately, in the 2nd edition the authors decided to reimplement the BASIC examples as java applets hosted on a site that is no longer available. So I should have been more specific that the 1st edition with the cool BASIC examples is now out-of-print.
Q: What does the B in Benoit B Mandelbrot stand for?
A: Benoit B Mandelbrot.
;-D
I read the question then the answer, then went back to the question, then read the answer again, then back to the….. Did that 3 times before I realized it was a fractal question… well played sir.
In the 80’s there was a software running in DOS called Fractint. It was fascinating to zoom in the Mandlebrot set graphics.
here’s a link to that on youtube: https://youtu.be/0jGaio87u3A
Fractint is still around.
http://www.fractint.org/
FractINT was the first program to use the GIF 89a image format. For some fractals it can pause and store the progress in the GIF image file. Quite important when rendering on a slow 80286 or 80386 without a math co-processor.
The origin of FractINT was to prove it was possible to generate fractal images using only integer math, without a floating point co-processor.
fractint uses fixed point math, which is very efficient and pretty fast.
I’ve got the source somewhere around here if you want to have a look, it is great example of doing things with limited resources.
POVRay was another great example of clever fixed point math usage
Problem with Fractint is, well, the int. It means it loses detail if you zoom in too much, and zooming into Mandelbrots to find more Mandelbrots is 90% of the fun. So they’re not technically fractals.
Last time I tried it was about 10 years ago and it still had the problem. May as well do it as Fractfloat now anyway, with so many FLOPS in modern PCs.
It was a nice repository for various trippy graphics generators though, had CA and Langton’s Ant and all sorts of stuff squeezed in, it had an extensible format so people could just add new algorithms, and they did.
To add some higher dimensions, my brothers youtube channel (https://www.youtube.com/channel/UC2IhPOfKICJW-vfkrbbLqBw) has some fancy 3d fractal videos, including stereographic ones and a few 360° videos (try with cardboard + smartphone).
If you want 3D fractals, they’re called “quaternions”. Or at least something very similar to them is.
mandelbulb3d is also fascinating. Takes hours to render a short video or a single high resolution image, but I think it’s worth it.
Is anybody aware of 3D fractal generators that can display the fractal in real time using OpenGL or something like that to avoid CPU-only rendering?
A Google search says yes, there are, apparently shaders can do some fractalising. I wouldn’t have thought it was possible, since 3D cards deal in regular polygons. But it is! Might give some a try, see how fast they can go. I was impressed on an AMD 1.7GHz a few years ago, a bunch of new Intel cores in this one should give it a shake. Fractals are something that benefit from multiple cores easily, since it’s a bunch of independent equations (well, Mandelbrot is). I suppose the floating-point maths is something within the reach of 3D cores.
Should keep me occupied for the afternoon!
Actually I bet cellular automata would be fantastically good on a graphics card. Modern CAs use special techniques to reduce the number of calculations needing done, caching certain areas for re-use if the same configuration pops up later, and keeping track of the active area, ignoring blank areas. They were amazingly fast too, a big Conway was hundreds of generations / second, and that was on my old computer too.
Really ought to get round to programming my idea for an L-system editor. The idea is, you enter your L-system by manipulating lines and nodes with the mouse, rather than having to think up an algorithm and type it in. I suppose Javascript is as good a language as any, bit rusty with it. I’m surprised nobody else has had my idea, seems obvious after spending time with existing L-system software (what little there is). Should allow much more flexibility and subtlety, as well as real-time updating as you tweak.
If I get stuck I’ll nick some turtle graphics code from LOGO somewhere. It’s just sin and cos to convert polar to Cartesian.
Are there any decent, free C compilers for Windows btw? DJGPP was good, though it had limitations, bit short on the extra features. But that’s obsolete now I think. Still was nice to use Vim and DOS scripts instead of some cheezy IDE.
Or maybe I’ll polish up my Java.
Quaternions are something else actually – they’re four-dimensional complex numbers. The standard two-dimensional ones are of the form a+bi, while a quaternion looks like a+bi+cj+dk (where i≠j≠k, yet i²=j²=k²=-1). They’re commonly used to represent rotations of objects in 3D space.
Though yes, the next step up from the standard Mandelbrot set would exist in quaternion space, not the 2D complex plane. But that makes it 4D, not 3D. (https://www.youtube.com/watch?v=afa7lU_yHy8)
A direct 3D analog of the Mandelbrot set is nonsensical, mostly because the math for a 3D complex space doesn’t quite work out. 3D fractals of other kinds do exist of course – the mountains generated above are one example. Mandelbrot, and others in the Julia/*brot complex space family aren’t the only ones.
Ok. But there are fractal quaternions, I’ve seen the renderings even if the maths is a bit beyond me. They’re rendered in 3D but yes, are 4D. Somehow.
Fractals as called fractals because their dimension is not a whole number. A true (n) dimensional fractal has a structure that approaches (n+1) dimensions.
The reason that fractals are applicable to antenna is that they contain geometric harmonics which can be tuned to match multiple bands, or a boarder spectrum than a simple structure can resonate with.
a targeting system idea I had for my “robot army of doom”, is to look at the outline of an object.
Human made things have a fairly “simple” outline, natural things have a complex outline.
so far I gotten edge detection happening, but actually measuring the outline is harder than I thought!
“So it’s got a few bugs!”
If they ever try take over the world, at least the coastline of Britain will keep me safe.
Not sure if its technically “fractal”, but Terrence McKenna had his time wave zero theory that expressed a relationship between time and novelty. Sure, he was wrong about 2012 but the idea is still interesting.
Terrence McKenna was a buzzword-spouting drug-addled halfwit, who it was briefly fashionable, among a small group of 90s acid-heads, to take seriously. Or maybe they were being ironic and taking the piss out of him. Hyperspace machine elves probably aren’t the secret of the Universe.
I wrote my own fractal and Mandelbrot generators in Turbo Pascal in ’93-’94 for my Senior Seminar and Honors Projects when I was finally wrapping up my degree. I used James Gleick’s book Chaos:Making a New Science as my source for the SS project. Did the Sierpinski triangle and carpet, self-similar dendritic trees, and of course the Mandelbrot set – with homebrew save and restore option.
For the Honors Project I grew dendritic copper crystals in a Petrie dish full of CuSO4 and using solar print paper and a flatbed scanner, (this was ’94, remember?) digitalized them and compared the fractal dimension of the simulation to the 2D projection of the actual dendritic shape. I used an old PC power supply for power, and gave the class that would be doing the Honors project the succeeding year a demo. One student asked Prof. Sweeney in a horrified voice, “We aren’t going to have to make EQUIPEMENT, are we?” Tom Sweeney was my advisor, and said with a laugh, “No, Edgar is just kind of an overachiever.” Good times. A+ in both projects. With the graphics libraries available today, rolling your own should be pretty straightforward. I also recommend Fractal Programming and Ray-Tracing with C++ by Stevens, which might be a bit dated.
Fractal math was used to create the landscape and buildings of the planet Ego in “Guardians of the Galaxy Vol. 2”.
amongus