I have a confession to make. I enjoy the challenge of squeezing software into a tiny space or trying to cut a few more cycles out of a loop. It is like an intricate puzzle. Today, of course, there isn’t nearly as much call for that as there used to be. Today even a “small” microcontroller has a ton of memory and resources.
Even so, there’s still a few cases where you need to squeeze those last few bytes out of memory. Maybe you are trying to maximize memory available for some purpose. Maybe you are anticipating mass production and you are using the smallest microcontroller you can find. Or maybe you’re doing the 1 kB Challenge and just want some advice.
One way to find techniques to maximize resources is to look at what people did “in the old days.” Digital Equipment computers once had a special character set called Squoze (or sometimes DEC Radix-50). This technique can be useful when you need to get a lot of strings into memory. The good news is that you can reliably get 3 characters into 2 bytes (or, as DEC did, 6 characters into 4 bytes). The bad news is that you have to pick a limited character set that you can use. However, that’s not always a big problem.
The Big Blue Connection
The key to Squoze is that you have to pick 40 characters that you want to encode. That’s enough for 26 letters, 10 digits, and 4 punctuation marks (a space plus whatever else you want). Notice that 26 letters means you have to pick upper case or lower case, but not both.
You might wonder why it was called DEC Radix-50 if you can only have 40 characters. The 50 is octal (base 8) which is 40 decimal. The Squoze name was actually used both by DEC and IBM. In the IBM scheme, though, a 36-bit word held two flags and 6 characters from a set of 50 (decimal 50, this time). Historically, the use of Squoze for symbol tables is why a lot of old compilers used 6 character symbols with only certain allowed characters (if you ever wondered about that).
How it Works
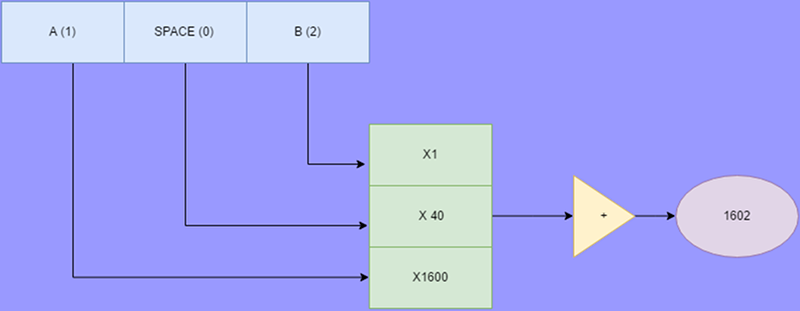
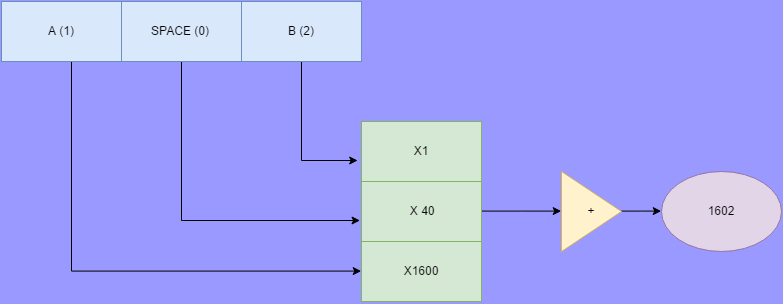
Once you have 40 characters in mind, you can treat them each as a digit in a base 40 number. Hold that thought and think about a regular decimal number. If you have a string of digits from 0 to 9 coming in, you can build a decimal value like this:
value=0 while not end of digits value=value * 10 value = value + digit end while
If you have the digits “643” then the value will progress from 0 to 6 to 64 to 643.
If you generalize to base 40, the “digits” are numbers from 0 to 39 (representing a character) and the *10 becomes *40 in the above pseudo code. If you prefer, you can think of it mathematically as the first digit is multiplied by 40 squared (1600), the second digit by 40 (40 to the first power), and the final digit by 1 (40 to the zero power).
Suppose, then, that we select 0 to represent a space, 1 to represent an A, 2 for a B, and so on. The string “A B” (that is a space in the center” would be 1, 0, 2. Running through the algorithm, the result would be 1602.
Decoding is just the reverse. Starting with 1602, for example, you do an integer division by 1600 to get a 1 (A). Take that away leaving 2. Dividing by 40 gives you a space (0). Then there’s 2 left–a B–so the string is “A B” as you’d hope.
Why Forty?
Why go through all this trouble? Why use 40 and not, say, 41 or 50? Think about the largest number you can represent with three base 40 characters. 39*1600+39*40+39 = 63999. That fits in a 16-bit word. If you went with base 41, the largest possible number is 68920. That’s too big for a 16-bit number.
The point is, using this scheme you can pack 3 characters (from your set of 40) into two bytes. Compared to normal ASCII characters, that’s a savings of 33%. Not much, but compared to other compression schemes it is simple to implement and it always saves 33%. Well, at least, roughly. If your text length isn’t evenly divisible by 3 you may have a padded character or two which reduces a little efficiency depending on the total text length.
Imagine a bunch of LCD menu entries stored in EPROM. Saving 33% could leave you some room for more strings or more unrelated features. Of course, you also need to factor in the size of the code and the character table. Frequently, you don’t need both encoding and decoding at run time, but there’s still some overhead to consider. You have to evaluate your needs and decide appropriately.
Enhancements
If you chafe at the 40 character limitation, you can pull a few stunts to get more at the expense of possible efficiency loss. For example, for some applications, you can assume the first letter of a string is uppercase and the rest are lower case. Or select your 39 most common characters, use one more as an escape character and then pick 40 more for a total of 79 characters. You could use the escape character as a “shift” character, too, if that works better for you.
Implementation
You can find a simple C-language implementation on GitHub. The make file generates two executables, one for encoding and one for decoding. You can define a symbol to avoid building the executables if you want to experiment with the code as a library.
The encoder and decoder will use a default character set if you like. You can also provide one yourself. The code is hardly optimized so if your application shares code and data space, you probably want to spend some time paring the code size down. However, for a demo or if your code space is separate and plentiful, it is probably good enough as it is.
The code is set up so you can run the encode and feed its output to the decoder:
$ ./encode | ./decode Hello Hackaday. A man, a plan, a canal, Panama. Characters in=48 (13012) HEL (19800) LO (12843) HAC (17644) KAD (2637) AY. (40) A (20854) MAN (60801) , A (652) PL (2198) AN, (40) A (4854) CAN (2118) AL, (641) PA (22453) NAM (3080) A. Bytes out=32 Full String (length=48): HELLO HACKADAY. A MAN, A PLAN, A CANAL, PANAMA. $
Note that the characters are shifted to upper case by the encoder.
Worth It?
This is just one more trick to put in your toolbox. It isn’t for every project. You need to be able to live with the limitations. You also have to be able to accept the additional code and the runtime overhead. Depending on the data you have, there may be better options. For example, a data logger might store floating point numbers or some other scheme.
Huffman encoding, run length encoding, and other methods might do better–it depends on your application. However, I do think it is interesting to mine some of the old techniques and apply them to new solutions.
If you had fun with this, you should throw your hat in the ring with the 1 kB Challenge I mentioned before. Hackaday wants to see what you can do with a 1 kB compiled binary limit for a microcontroller-based project. Give it a shot and learn the space-saving techniques of old along the way.
















I wonder how hard it would be to limit yourself to fewer characters to get a higher compression rate. If you only want text you could do 28 or less, if you do not use all 26 characters that is.
You kinda need 38 char$. Forgot numbers?
You can always spell numbers…
You don’t have to use numbers.
Except the digits l and O (remembering my parents’ typewriter)
hey h a d you forgot null terminationh7 468trh 4tr86h 4t358
Funny. Usually with these you had a fixed number of characters. This is why a lot of compilers had 6 character symbols with no spaces.
You can just pad out your strings with spaces.
You don’t need null termination. Just prefix all your strings with their length. You tell things upfront how long your string is.
Another storage note: Late-70’s/Early 80’s Data General mainframes had a 60-bit word in which 10 characters in a similar character set could be stored as a short string.
Not to mention the penchant for overloading variables — especially booleans — as sets of bits in a byte or word-sized integer, the good ol’ days required a lot of creativity to fit within minimal memory models. Remember that first-gen home computers (Apple II, TRS-80) had 4K RAM. The original Mac had 128K (and the OS, MacWrite and MacPaint could all fit on a floppy). I’m still astounded that simple apps on my phone take up multiple megabytes. Oh, and get off my lawn.
“Get off my lawn” takes too much space. Will have to trim that off. :-)
Macintosh worked around the small RAM size by packing a lot of the operating system into the ROM, especially the graphical parts of the GUI.
Not Daya General, but Control Data.
I have fond memories of developing a database system for the original IBM PC. Even after generalizing menu systems and using data segmentation the program size started to interfere with the data size we could handle. So I wrote a “cruncher” program that took a .BAS file and shoved non-branching lines together, stripped REMarks, etc. It bought another year or so of use out of the same PCs. Didn’t get down to the byte level, but it was curious to pre-parse an interpreter language.
A lookup table may not actually be required on many systems. If you’re reading or writing to a device that understands ASCII, then ASCII’s human-readability may come in handy. You’ll notice that a lot of the alphanumeric stuff is sequential, so all you really have to do to get the value for each character is truncate the ASCII representation and shift through the space by adding or subtracting an offset. This is also a reversible process, and is something you can do every time you read or write a character to an ASCII device. After all, the table is only needed to translate into and out of your internal character set, which you probably only need to do when talking to an ASCII device.
Another option, BTW, is to do everything in baudot. It’s slightly more compact, at 5 bits per character (5*3 = 15 < 16), and there already
sexistexist devices that naively understand it. Not only was it used for teletypewriters, but a lot of machines read and wrote to baudot-encoded paper tapes. All you need to do is hack the interface.Dang spell check. replace ‘sexist’ with ‘exists.’
I’ve read a lot of election news, cut be a break.
Replace ‘be’ with ‘me.’
I have no excuse this time.
Be nice if this forum had an “edit” function.
An often requested feature. For now, I am the edit button
@M: I fixed your ‘sexist’ autocorrect problem ;-)
Nah, misspelling when correcting the initial error is actually encouraged.
Thanks for the mention of baudot; I started to get lost in Wikipedia links!
“cut be a break” is acceptable, sort of, as a cut is a break… and maybe you had a “toad” (cold) and were typing it as you would speak it?
Wonderful how the lasting effect of this post is to make people marvel at my terrible spelling.
ಠ_ಠ
Joel, you are thinking of Control Data (CDC) perhaps – no 60bit machine in Data General’s commercial offerings.
Univac 1100 series also had 6 bit symbols – 6 per 36 bit word. Aah, memories… or are those nightmares?
I did a lot of time on an 1108. That was Fieldata: http://nssdc.gsfc.nasa.gov/nssdc/formats/UnisysFieldata.htm
PDP-10 called it “SIXBIT” when they packed six characters into a 36 bit word. This was used for filenames, for example.
Ah. Fond memories of RAD-50 file names on RSTS/E.
There is no such thing as a fond RSTS/E memory!
If you go this way, you have also to account for the decoder size (might not worth the trouble in the end). You should also read about the arithmetic coding scheme since this is a kind of (very inefficient) arithmetic coding…
You can also use LZSS compression, which I’ve used on 6502 when writing code for size-constrained competitions (though in that case it was a 4k one): http://www.deater.net/weave/vmwprod/tb1/tb_6502.html
I have size-optimized LZSS implementations in 26 types of assembly language if anyone wants them: http://www.deater.net/weave/vmwprod/asm/ll/
LZSS in asm for 26 architectures! Cool. (Oh you said that. I misread as “26 bytes of…” :-) )
Fascinating that Thumb and Thumb2 come out so close in size.
Thumb2 is only a win if the code in question doesn’t map well to regular Thumb. With something relatively simple like LZSS decoding (that doesn’t use many registers or large constants) it didn’t help much.
I’ve been meaning to get some more architectures out, especially risc-v. Just haven’t had time :(
Very nice idea!
You could also use of the 1536 characters between 63999 and 65536 in a special way to encode EOF (end of file), CR (carriage return), LF (line feed) or a CRC (cyclic redundancy check) check sum. This can be really interesting when thinking of arduino and co. Your “cipher” is kinda block-chained with same distances of 16 bit, so the code can be implemented simple.
But I think a dictionary based algorithm will easily reach much higher compression rates due to Zipf’s law, which also would be harder to implement efficiently and as flexible.
You can do that but it hurts efficiency. If you have one stray character you wind up having to pad it worth spaces and then blow another two bytes for your special code. Depending though tush might be OK for your application. Just something to think about.
Squoze instantly reminded me of this https://www.pinterest.com/pin/562668547164443686/
Has anyone ever used Morse code in a computer program?
No.
Many times to blink out data
Could get some bit reduction with Morse by using 0 for dot and 1 for dash. That makes all numbers only 5 bits and letters are 1 to 4 bits, with less commonly used letters using 4 bits.
But how do you pack Morse code into an 8-bit architecture while still knowing where the breaks between characters are, especially if you aren’t padding it all out to 5 bits per character?
Morse code really isn’t suitable for compressing text, BECAUSE you need additional bits to encode the length of the character, and it just gets messy if you also have to consider very long codes (at least as many as seven elements, off the top of my head) that are rarely used. It’s much easier to do in ternary, because you can use 0 for dit, 1 for dah, and -1 for stop. But of course, you have to convert from ternary to binary if you’re going to store it. If you want to do this in 8-bit bytes, you have 256 codes available. In ternary, 5 digits have 243 possible codes, which fit nicely into 8 bits. So you can encode five ternary digits in each byte, which means that all letters will fit into a byte or less, but numbers and punctuation won’t.
If you want something simpler, you can use two bits to encode each element. This seems wasteful, but keep in mind that with four codes available, you can have 00 = dit, 01 = dah, 10 = ending dit, and 11 = ending dah, so you don’t need a separate code to indicate the end of a character, and all letters can still fit in one byte. But numbers and punctuation end up taking more bits, I think.
To use single bits for dit and dah as you suggest, you can prefix each character with a fixed field of three bits to store the symbol count, then letters and numbers all fit into 8 bits (3 bits count + 5 or fewer bits data), but then there’s hell to pay if you have any characters that take more than 8 symbols.
All of these schemes require using variable-length bit fields to have any chance of saving bits, which nobody likes to do. The approach Emile Baudot used in mechanizing telegraphy, was to use a fixed number of symbols (5) per character, and special “shift” codes to change back and forth between the alphabetic and non-alphabetic codes.
It’s this kind of thinking that leads to code that breaks in ways nobody can figure out. In most cases, it’s easier to use fixed-length codes, along with a generalized compression algorithm. This way you have only ONE “clever” algorithm to support.
So… this is basically a look-up table with some shift-left/shift-right of data bits? Maybe I’m too old but this seems like basic stuff to me.
That’s a blast from the past — I used Rad50 on a project long ago to save space (back when it mattered). We stored part numbers that way, and I told them they could have A-Z, 0-9, and just 4 punctuation characters which we argued over for a week.
That is a pretty complicated way to say that DEC used 3 bit nibbles and octal (0 to 7) instead 4 bits and hex. Given the speed of the machines then, and the instruction set, a lookup table is a lot faster than that algorithm. I never saw anything used but LUTs, unless RAM was insanely tight. In fact, a LUT is faster for determining things like upper versus lower case, or case conversion, or multiplying two nibbles, and not very big.
Yes, DEC liked their octal, and used it even on 16-bit machines where it was really kind of awkward. The only architecture I’ve ever seen that was a good match for octal was 8080/Z-80, where you could actually learn to assemble programs by hand pretty quickly because almost all instructions used a two bit field plus two three-bit fields. No, DEC picked 36 bits for the machine word because .. reasons, and then cramming six characters into each word was just a more elegant (?) solution than packing five 7-bit ASCII characters in, and throwing away the extra bit. Which is another way strings were done on the PDP-10 IIRC. The 10 also had some byte-oriented instructions, but not for bytes as we know them. These were used for unpacking “bytes” of any length. You specified the byte length, the address of your string, and the number of the byte you wanted, and it would do all of the hard work and return that byte. Because programmers were always doing weird bit packing things to save a bit here and a bit there. Which I guess made sense, since on a 36 bit machine, you could be throwing away a LOT of bits if you weren’t packing everything you could think of into each word.