People learn in different ways, but sometimes the establishment fixates on explaining a concept in one way. If that’s not your way you might be out of luck. If you have trouble internalizing floating point number representations, the Internet is your friend. [Fabian Sanglard] (author of Game Engine Black Book: Wolfenstein 3D) didn’t like the traditional presentation of floating point numbers, so he decided to explain them a different way.
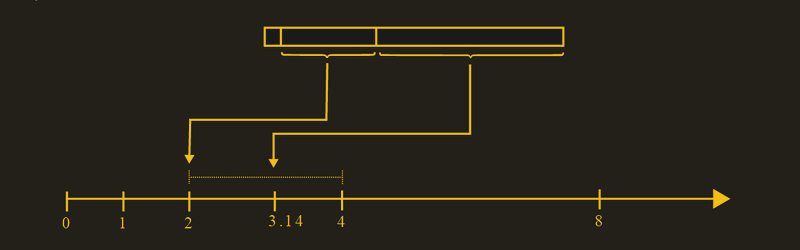
Instead of thinking of an exponent and a mantissa — the traditional terms — [Fabian] calls the exponent as a “window” that determines the range of the number between two powers of two. So the window could be from 1 to 2 or from 1 024 to 2048 or from 32768 to 65536.
Once you’ve determined the window, the mantissa — [Fabian] calls that the offset — divides the window range into 8,388,608 pieces, assuming a 32-bit float. Just like an 8-bit PWM value uses 128 for 50%, the offset (or mantissa) would be 4,194,304 if the value was halfway into the window.
There are a few details glossed over — the bias in the exponent and the assumed digit in the mantissa are in the provided formulas, but the reason for them isn’t as clearly spelled out as it would be for the “classic” explanation. If you want a go at the traditional classroom lecture on the topic, there’s one below.
We’ve talked about floating point representations and their effect on missiles. There was a time when you hated to use floating point because it was so expensive in either dollars or CPU time, but these days even a solder controller can do relatively fast math with floats.















Great now I know I’m too dumb to understand it in two different ways. I guess I get sorta how its accomplished but I don’t understand if loosing a bit of precision is ok why can’t you truncate or round of the number instead of floating point?
Well the choice is integer math only, vs some kind of floating point implementation, so you may as well make it a good and robust one that you can go from those infinitesimally small physical constants to the number of atoms in the universe, rather than being limited by your number of bits, or using integer only and ending up trying to make things work with pi equal 3.
“Fixed point” is commonly used in FPGAs.
Say if you only need precision to the nearest 0.25 you might use 14 integer bits and 2 fractional bits.
Fixed point is very useful for sprite engines on limited platforms like the Gameboy. It was a real eye-opener for me when I discovered it.
I worked from TomTom, all SATNAV’s use fixed point, 8.24 format. Floating point can’t cope with Lat / Lon and creates errors if you try to plan a route too far away from the origin, which is most of the land on the earth. Also on the cheap chips used, a lot faster LoL. Floating point is so bad that to render in 3D we kept the camera at 0,0,0 and moved the world around it. (GPUs matrix mul would break is not)
@[Mark]
Any links? That sounds very interesting.
Integer math is so much faster than floating point math (even if you have an FPU). A lot of microcontrollers can do any integer operation in one or a few clock cycles, whereas a floating point operation might take several 100 cycles. A lot of times, you can get away with a result that is “good enough”, especially if you work with real-world systems. Your hardware is going to be the least exact component in your system. What I usually do simply scale down my numbers (for example that I work in millivolts instead volts, or micrometers instead of meters or millimeters).
You can look it up for chips like STM32F4XX and compare (assuming if you need faster floating point you use floating point hardware). For instance, integer multiply is 1 cycle and divide is 2 to 12 cycles. Floating multiply is 1 cycle and floating divide is 14 cycles. And you get DSP instructions like mul and add to accumulator that take 2 cycles.
Oh actually I replied to the wrong thread. I was meaning to reply to RW talking about the x87… oops.
Some processors (the Alpha comes to mind) had FP divide units but no divide in integer. So in that case, a FP divide was faster than doing a divide algorithmically. Also, a lot of the FPUs now can at least match the integer unit for speed in many cases.
But yeah, generally true, just not always.
Yah seem to remember a glaring omission in some member of the x86 series, where it “couldn’t even” without the x87
The 8086 had an external co-processor (8087) that had a FPU. Likewise the 80286.
The 80386DX had the co-pro built in or you could buy a cheaper variant 80386SX that had no co-pro
The 80486 onwards all had an inbuilt co-pro
No you still needed the 80387 with the DX, it just mainly had higher address range over the SX
There were some weird combos around too, mostly due to the interstitial periods where there was an x86 available but no x87 … So you got some boards that would take a 286 and a 8087. For the 486SX, the 80487 was pretty much a DX that just disabled the SX.
It also looked weird when you had a Cyrix 486SLC or something which was really a three and a half eight six, working on a 386 bus and those worked with the Cyrix fasmath 387… which actually was fast in the day, ppl wanted them over the intel one. But then you’d get them on an interposer to fit in a 486 board, and IDK if there was any way of using the 387 then. Not that many 487 capable boards were sold because ppl soon figured they could just as easily swap out the SX for a DX, usually cheaper too.
The difference with the 80386 (onwards) was that there was no discreet co-pro. If you plugged a 80386DX into the second socket of a 80386SX mainboard then it would completely disable the 80386SX.
Also Cyrix made a 5×86 when intel was still making the 80486 and the cyrix chip was much faster. Then intel switched to CPU names instead of numbers as you can’t patent a number and you can’t predict what is next in a series of names.
Ok so I had to go dig this up: http://collaboration.cmc.ec.gc.ca/science/rpn/biblio/ddj/Website/articles/DDJ/1993/9306/9306d/9306d.htm
This really depends. For scalers, integer math will win out every time due to less steps needed to accomplish the math. For vectors and matrices however floating point will win on certain hardware like that used in GPUs. It’s not that they are bad at integer math, just that they have really freaking awesome tricks to do a bunch of floats in bulk that only really work when you do a bunch in bulk.
Fixed point math minimizes absolute error. Floating point math minimizes relative error.
For example, in integer math the value will always be +- 1 units accurate. In 32-bit floating point math, the value will be +-0.000 006 % accurate. Real world situations tend to be so that +- 0.000 006 % rarely matters, but you have to choose your units carefully to make +- 1 unit not matter.
If you use integer math with micrometer units in a geometry calculation library, one day someone will try to load up a microscope image and suddenly it just isn’t accurate enough anymore.
double_wide plankUnit = 0; // Cause 10^-43 is “good enough”
You would need at least 144 bits to cover whole range of 10^(-43) to 10^43 in those units. Is it enough?
You never know without a concrete application. Is it possible that a temporary result will be outside that range? Can it be corrected by rearranging calculations? It all depends on what your algorithm does.
No. 144 bits wouldn’t be enough. I’d go with 256 bits to be on the safe side. That would give me extra clearance, along with some bits to attach color, transparency, and a pointer to texture to as well.
To be on the safe side, I’d go with 384 or 512 bits.
Rational arithmetic is perfect.
What does a standard PC use? Base 10 or Base 2? I thought a PC used Base 10 and a FPU uses Base 10.
Also quote [Al Williams]: “Just like an 8-bit PWM value uses 128 for 50%”
There is no 50% for PWM as there are an even number (256) of graduations and therefor no middle. The closest to the middle are 127/255 and 128/255 which are equally close to the middle but neither are *at* the middle.
R2R is different in that all ones does not make it to the reference voltage. ie If +V(analog) = 2.56Volts then 11111111 or 0xFF will be 2.55Volts so 1.28Volts is half of +V(analog).
ADC is much the same that 128 or 0x80 is half +V(analog) but likewise the maximum sample value is 255/256*+V(analog).
Every base is base “10” when written in itself ;)
Computers use binary, of course.
128/255 is 50%, accurate to zero decimal places… Al didn’t say 50.000%
Yep it’s 50.0196%
I’ll pay that as a well thought out and correct response!!!
Well it depends on how you do your PWM. If you do it “in parts” like an ADC, then yes. However, many PWM generation algorithms work like this:
1) Take the PWM value
2) Add it to a running total
3) Take the carry bit as the output
So if you take 128 you get this sequence of counts (output)
0 (0)
128 (0)
0 (1)
128 (0)
0 (1)
So assuming the paths are equalized it IS 50%. If the PWM value is 1 you get:
0 (0)
1 (0)
2 (0)
…..
255 (0)
0 (1)
Or really 1/256.
If you have 255 you get:
0 (0)
255 (0)
254 (1)
253 (1)
….
0 (1)
255 (0)
….
So really 255/256.
And in any event, even by parts, the 128 is “about half”.
Interestingly, my PAK-V can produce both kinds of PWM (but not at the same time). For most people, the factor is that the “by parts” method gives a constant frequency. The other method has a range of frequencies and always generates as fast a pulse train as is possible given the base cycle time. In other words, if your “tick” is 1 ms. 50% on “by parts” or “equal area” is 128mS on 127ms off. If you use proportional then 50% has 1mS on and 1 mS off. But the frequency slows down as you go further from 50%.
Is that PAC-V a Parallax Propeller? I would probably have used a simple CPLD to do much the same.
You may have looked at this but … have a look at Bit Angle Modulation it take a lot of the load off the CPU in a micro-controller if you don’t have hardware PWM.
No the PAK-V core is the now defunct Scenix SX. When I run out of stock they are gone forever ;-)
And actually, I did a PWM generator for N&V on a CPLD and we posted a CPLD peripheral in one of my Lattice IceStick tutorials (an FPGA).
As for BAM or BCM, see https://hackaday.com/2011/07/22/using-binary-code-modulation-to-control-led-brightness/
and
https://hackaday.com/2015/09/08/pulse-density-modulation/
Oh wow, that is one that got away.
I wanted to get some SX chips in the days of Ubicom but from memory I ended up with something called a Rabbit chip from somewhere else.
72MHz raw symmetric MIPS is a clock counters delight.
PWMs I’ve worked with usually have 256 “states”, 255 from the configured value and a dedicated OFF flag. As a PWM value off 0 sets the IO high for 1 of the 255 timer cycles.
The Atmel chips also have this. But, for example Arduino hides this from you by implementing 0 as OFF. Giving you 255 states, and going from off to 2 steps high if you go from 0 to 1.
So 128 could be 50%, if you go from 0 to 256 to define all states.
From 0 to 256 is 257 states. What I was saying is that there is no middle integer between 0 and any odd number like 255. What integer is half way between 0 and 3?
Why talk in decimal?
Stick it in binary and shift right, that’s half. :)
Only after dropping the LSb that was shifted out the right and rounded off. Had the LSb been 0 then the result would have been the same.
Now you have me trying to remember which was Shift Right Logical (SRL) and which was Shift Right Arithmetic (SRA)??
Does it not start at 0?
0 to 255 is 256 permutations.
What number is exactly half way between 0 and 255 … The answer is 127.5 which does not exist as an integer in an 8 bit system. So the closest are 127 and 128 or 0x7F and 0x80 or 0111 1111 and 1000 0000
I don’t think this is too hard to understand… I think you’re overestimating a simple problem.
what do you think?
Imho – bad explanation.
Why use word “offset” when you can use word “scale”? It’s as easy to understand as “offset” and it’s not such a misleading concept.
not the same. An offset refer to an addition/substraction. A scale refer to a product or logarithm. The exponent is a logarithm but internally it is represented with an offset. To get the exponent the offset must be substracted. For example in binary32 IEEE754 format the exponent is offsetted by 127 so to get real value of exponent one have to subract 127 from it. So if internally the exponent is represented by 254 the exponent to by applied to the mantissa is 254-127=127 . And if internal representation is 1 the exponent is -126.
Ah, the good old floating point that is both a bit of a pain to work with, even harder to implement in hardware, and generally overused in applications where it generally isn’t needed. Not to mention also being praised for how good it is supposed to be.
But if we consider that a 64 bit variable is already large enough to handle practically anything. And the few times it doesn’t, then have you looked at a 128 bit variable?
But it would have been so much nicer if the ones deciding on making floating point instead made Fractions, as those are actually having the same advantages, and lacks a few of the disadvantages. But, fractions is its own can of worms though…
And, straight up integers or fixed point have their disadvantages. Integers and fixed point tends to need huge variables to be practical in certain applications. (3D rendering isn’t such an application though, as just think of it, a 64 bit variable can tell the difference of one nanometer in the span that light travels during one minute in vacuum.)
And fractions are technically easy to implement in hardware, and can explain both small and large numbers with relative ease. Not to mention never having a need to be divided. As division is done through multiplication. But I wouldn’t be surprised if one could make a long list of disadvantages with Fractions, but comparing it to Floating point is the more interesting part.
I see the advantage where one could instead of using a few million transistors on an 64 bit Floating Point Unit build a 64 bit “Fraction Processing Unit” instead for around 250 thousand transistors instead. That could technically give a CPU more math crunching resources that could be of more use to the user. Or give the processor other features and or more cache memory or something….
By “fractions”, do you mean rational arithmetic?
Yes.
It has similar advantages to Floating point as it can both explain a large number like: 4294967296/1
And at the same time also being able to explain a small number like: 1/4294967296
This is if we were to only use two 32 bit variables. This effectively gives us the resolution of 32 bits, but the span of 64 bits. Downside is that this simple implementation is far from efficient though.
We could do it a bit more efficient by first having a few bits that inform how the rest of our bits should be distributed to form our two terms. We could for an example have 64 bits, where the first 4 bits tells us how many bits belongs to A, and B respectively, where the fraction is A/B. So if our 4 bits are having a value of 0, then we for an example know that we have 0 bits in A, and 60 bits in B, and then we can by definition call this 1/B. While if our 4 bits are 15, then we say that our 60 bits belong to A, giving us A/1 instead. And if our 4 bits are having a value of 8, then we have the first 30 bits in A, and the other 30 bits in B. Downside here is that 60 isn’t really dividable by 16 in any nice way, not that it is technically a problem, it just isn’t nicely implemented.
Nicest implementation in an 8 bit system handling 64 bit variables that I can see is to have two Fractions, each being 64 bits, where we have one 8 bit byte representing the distribution of each of the two stored Fractions. As then our byte can be split into two 4 bit variables, each of them dividing one of our 64 bit fractions into 16 segments. Downside is if we have an application where we have an uneven number of variables…. As that would lead to an extra 68 bits being wasted. But considering how RAM is allocated on modern systems, then 68 bits is almost nothing.
And another downside, these extra 4 bits per variable is chewing up our memory, but we technically get 4 bit higher resolution in our calculations.
And also, if we end up in a situation where we have two fractions that when calculated would create something that has overflow, then we still need to do a bit of rounding, we only have a certain resolution in our bits after all.
And we can do two forms of rounding, one is trying to find a common dividable number that we can take away from both terms in our Fraction. This is technically lossless, but will eventually not work, as we run out of resolution.
The other rounding method is to simply cut off a certain number of bits from both terms, as an example:
In an 8 bit system we have the fraction 185/145 and in binary that would be 1011 1001 / 1001 0001
Here we can cut off three least significant bits, giving us 0001 1011 / 0001 0010
And that is 27/18 and that is though 17.5% too large, so this example were not really a good example. But generally, one wouldn’t cut off 3 of 8 bits. As that is almost half of our resolution.
As if we only cut off one bit, then we get 94/72, and that is 2,3% off from what we had originally. But still 8 bits isn’t much to start with. One would expect better results with larger variables.
And this here is probably the longest “yes” I have ever written…. I surely need to learn to be more concise.
I gave a paper on Rational Arithmetic at FORML one year. The primary problem at the time was how quickly the common denominators grew in size. With the amount of RAM today, you can go further and a lot faster, but the sizes accelerate quickly. For a well defined problem you can’t get any better. For general purpose it gets out of hand quickly.
Yes, that is a problem.
So at some point one just needs to call it good enough and start to do rounding where one looses resolution. And in a system using a lot of bits, then the rounding would only make a small difference. But still, it is a rounding error, so not good for all applications.
But as a comparison to Floating point, then both systems have an end to their resolution on arbitrary values. but fractions do have the advantage that it can do (1/3)*(8/17)+(3/11) with perfect resolution. but if we start adding on terms, then it will as you say grow out of control, even if we were to look for the lowest common denominator.
Positive side is that fractions are far easier to implement in hardware compared to floating point. Both in terms of simpler logic, and fewer transistors to get the result with roughly equal resolution.
But both systems do have a rounding error, and only has a fixed resolution. Even though fractions can flawlessly express a strange value like 922434148/293619911 with relative ease. And no that isn’t pi, but it has a rather long period before it repeats.
I at least think that Fractions are a nicer solution then Floating point. But non of the solutions are perfect in practice.
But making calculations in practice with Fractions probably have downsides that floating point doesn’t. After all, a different implementation can have superior performance in certain applications. I haven’t looked into if Fractions are good (as in on par with floating point, or better) for fluid dynamic simulations, 3d rendering, logic flow or other applications, maybe floating point is better in some of these, and that wouldn’t surprise me.
Though, at the same time, if we see that floating point would cut down the processing cycles needed by half, then we still use less then one tenth as many transistors to work with fractions, so nothing stops us from working more in parallel.
And yet again, a lengthy response where I mostly ramble on yet again….
I wanted to make a little calculator for American style fractions of inches for wrenches and steel and nuts and bolts and all that.
Got as far as exponent = window then left it. We have enough people inventing names for stuff that is named already like daughter board = shield etc etc.
The long term effect is confusion.
Yep, I will put that in my quasi-nuclear phase locked loop synthesized equalizer and smoke it.
I see no invention? Window used for describing a subset of values is common…
But I agree*, the proper word to use is of course base rather than invented stuff like “offset”.
(* /s)
Two *solid* introductions to computer arithmetic are:
http://people.ds.cam.ac.uk/nmm1/Arithmetic/index.html
http://docs.oracle.com/cd/E19957-01/806-3568/ncg_goldberg.html
If you want to use floating point arithmetic, you really should be aware of the contents of those documents.
Floating point arithmatic can byte you. :-)
3987^12 + 4365^12 = 4472^12.
Don’t read the next sentence of this post or anything after it. You just had do to it didn’t you, you rebel. :-) (This extra posting was made so I could check the “Notify me of new comments via email” checkbox, which I failed to do with my previous posting. Sorry for wasting your time. (webmaster – It might be nice to add that feature without requiring extra posts.)
But you also get bothered when some fool makes an inane comment on your post.
I guess that’s justice. :-) Its just to bad that I can’t click on that check box after making a post. post-posting?? WordPress seems to be effective, but sometimes it is just plain stupid. For instance when I did the first post, I was Rustin Lee Haase and then after that I was foxpup (an internet handle I’ve been using since when iomega zip drives seemed huge) Still, the price is right since it is free for me. :-)
The exact moment I lost the explanation:
“3 is 011, and the 0.25 is binary .01”
How is .25 .01 in binary?
Just the same as in decimal but with base 2.
So 0,25 in decimal is 2*10^(-1)+5*10^(-2)
and 0,01 in binary is 0*2^(-1)+1*2^(-2)
By extension of the existing binary system into negative exponents
2^4 = 16
2^3 = 8
2^2 = 4
2^1 = 2
2^0 = 1
2^-1 = 1/2
2^-2 = 1/4
2^-3 = 1/8
THANK YOU!
Extending into the negative was the mind gap I had.
I was always looking at the “left” side starting with 0, so for me anything that looked like “25” would always have to be “11001”, but yeah 2^-2 makes so much more sense :)
You don’t need exponents. In decimal, 0.1 is 1/10. in binary 0.1 is 1/2 and .01 is 1/4. 0.001 is 1/8, etc. Add them up as needed.
Is that your work?
You’re … eh em … *More experienced* than I thought.
Great article as usual! Thanks [Al Williams]
Which? Yeah I’m am old guy lol.
Sorry, my post went in the wrong place
This work here –
http://collaboration.cmc.ec.gc.ca/science/rpn/biblio/ddj/Website/articles/DDJ/1993/9306/9306d/9306d.htm
I was still in hardware then even though I wanted to do more programming.
Yeah I spent many years writing for Dr. Dobb’s may she rest in peace. I always straddled the hardware/software line. Some of my favorite work was back in the early 1980s when I did a 6805 board that was very versatile and then wrote the RTOS and the application software for it. Was used in a lot of stuff. Nowadays you’d just buy a board and RTOS off the shelf. I get that it is more cost effective, but it isn’t as much fun.
The 6805 didn’t have a lot of address space and you hated to spend a lot of decode lines for I/O. There was an LCD port that was write only. You had to do timing to the display’s maximum write time. The system EPROM read at the same address. There was also a bank switched UART and fixed point math ROM. You could do math or talk, but not both ;-)
I agree, the 80’s was far more fun in that you had to make things from the beginning. Back in the pre-internet days it was pure invention.
I was a bit of an outsider. Back then I went for the Z80 rather than the 6502. Now I use VHDL instead of Veralog so I’m still an outsider.
Congrats on the RTOS, I wrote a couple of very simple languages/OS’s. It great learning experience that younger people miss because it’s so easy now to just reach for a library that someone else has written.
We are too far nested for me to reply to you directly @Rob, but maybe it will sort out. Yeah I did a lot of Z80 mainly for the TRS80. I did some VHDL for my day job, but I do prefer Verilog mostly. As for RTOS, I wrote a number of them over the years ranging from some simple ones on GitHub to some big sprawling ones for the day job. I also did the PROT DOS Extender in DDJ (and my first book, DOS 5: A Developer’s Guide) which was mostly an OS. It’s claim to fame was that it was the first DX as far as I can tell that ran DOS and BIOS calls in V86 mode instead of rebooting to real mode and then rebooting again. At least 2 or 3 commercial products used variations of that technology after it appeared in DDJ.
You know you can still have fun like that, it is just harder to get someone to pay for it. I am in sight of a replica PDP8, a real 1802 and an emulated KIM-1/COSMAC Elf. Not counting how many other “old” computers that just aren’t on my desk right now.
As much as I loved the 80s I wanted to go back even further. I just wrote a post (not up yet) that references my old acquaintance Dr. Maurice Wilkes of EDSAC fame. He was a great guy and the stuff they did really was the foundations. You and me, we built on stuff that they dreamed up along with the others that came before us. Those guys were the pathfinders. I should do a write up on EDSAC sometime. I always wanted to an “authentic” FPGA replica (in other words, emulate the mercury delay lines in the FPGA and do a serial execution unit/ALU) and had corresponded with Wilkes about some of the design issues. He was very helpful, but I never got started on it and he’s gone now. I think he would have loved that. Of course, the university is rebuilding a replica that should be operational soon and I think there will even be Web access to it somehow.
Sorry… I’m rambling ;-)
The video shows encoding of the most-significant-bit of the normalized mantissa, but in IEEE floating point, that is left out (it’s always `1` for normalized numbers). Then I suppose you have to mention denomals, which opens up the door to infinities and NaNs, so I see why it was elided.
I agree that floats are often mis-used. A great example is 2D or 3D “worlds” like CAD or games. Do you really want your precision to cut in half every time you double your distance from an arbitrary origin? No, I didn’t think so! On the other hand, there are some things they are perfect for (e.g., linear light values in CGI, since perception is log-like).
In my line of work, I am very glad I learned how floats work. It has been very beneficial.
Wow! Great. I understood it very very clearly. Thanks a lot.