You can do a lot of electronics without ever touching a tensor, but there are some situations in which tensors are absolutely essential. The problem is that most math texts give you a very dry description that is difficult to internalize. That’s where [The Science Asylum] comes in. Their recent video (see below) starts with the dry definition and then shows you what it means and why.
According to the video, the textbook definition is:
A rank-n tensor in m-dimensions is a mathematical object that has n indices and mn components and obeys certain transformational rules.
That sounds a lot like an array but we are not sure what “certain transformational rules” really means to anyone.
Wikipedia does a little better:
[A]n algebraic object that describes a linear mapping from one set of algebraic objects to another.
These constructs are key to anything electromagnetic (including antennas) and show up a lot in stress calculations and quantum mechanics. Even Einstien’s theory of relativity uses tensors.
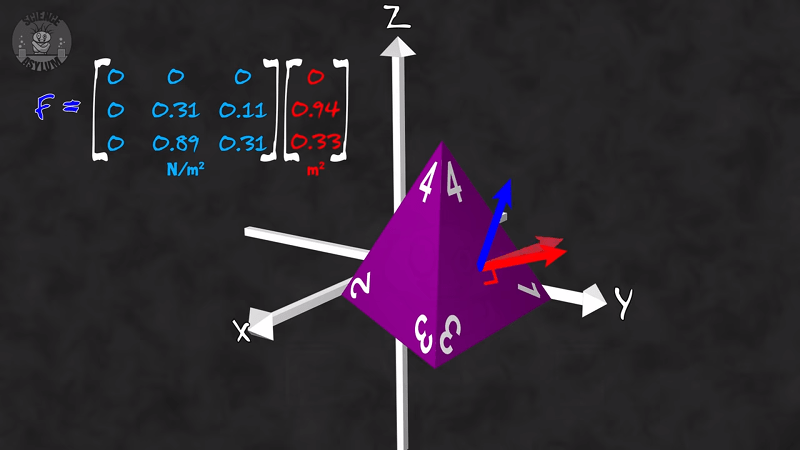
The video is a dozen minutes well spent. You even get some applications with tetrahedron dice and a basketball.
It is a shame, but a lot of math and electronics seem to be made harder than necessary. [Will Sweatman’s] series on calculus does a great job demystifying the subject. Then again, you could use a computer crutch, but that doesn’t help you understand, really.















I don’t know, a lot of texts seem to be made hearer than necessary.
Math classes have a reputation for being used to ‘weed out’ students from certain majors early on in the college education process. The ability of people to produce easier to understand lessons that are just as effective seem to lend credibility to that. Perhaps math texts are so bad because of the way math classes are being utilized by college faculty.
I learned my math much better through physics and engineering other than linear algebra. That I had an awesome processor for. And I wished I had learned it earlier. There are a LOT of topics in electrical engineering that, IMHO are easier to solve with linear algebra then the standard analytical methods. But most of my professors seemed to fear linear algebra :(
“but a lot of math and electronics seem to be made hearer” I assume you meant harder – and you are very right. I sometimes am teaching maths to adults (as a volunteer). I keep on getting “why didn’t they explain it like that at school!”.
The short answer to that is most teachers at school don’t really understand what they are doing, even if they can do it. Which means they a) can’t change what they need to teach to the right level to the person they are teaching b) they aren’t good at getting the essence of the idea across, as they don’t get it themselves…
“The short answer to that is most teachers at school don’t really understand what they are doing, even if they can do it. Which means they a) can’t change what they need to teach to the right level to the person they are teaching b) they aren’t good at getting the essence of the idea across, as they don’t get it themselves…”
HaD must be underappreciated then explaining all these “complex” ideas to the general public then.
We know that a vector has a length and a direction. The vector can be in two or three or more dimensions, but in all cases it represents one direction and one length.
What kind of object could hold two directions and two lengths?
In this case you can imagine an XY plane with two vectors at right angles, sort of like the hands of a clock. A clock with stripped gears so that you can set the hands at any position individually, but the clock model is a good one.
The two arrows can be represented by a matrix, where the two directions are the eigenvectors of the matrix and the two lengths are the eigenvalues. The determinant of the matrix is the two eigenvalues multiplied together, so while a vector represents a length, a matrix determinant represents an area. The area is the area of the rectangle between the two arrows.
If one of the vectors is zero length, then the determinant will be zero. This is a degenerate case that isn’t a tensor, so we see from this that a rank 2 (two vectors) tensor can be represented by a matrix, but not all matrices are rank 2 tensors.
The vectors within the tensor can be in 2 dimensions (2 x 2 matrix) or 3 dimensions (3 x 3 matrix) or more, but a matrix is always a rank 2 object and contains 2 arrows and two lengths, and is always square.
You can extend the model to three arrows: a rank 3 tensor is a cube of numbers, which might contain arrows in two dimensions (2 x 2 x 2 cube), three dimensions (3 x 3 x 3 numbers) or more. General relativity deals with vectors in 4 dimensions (x, y, z, and t) of various ranks.
The tensor is useful for keeping track of two (or more) forces at once, and the original use for such objects was in dealing with “tension” such as the surface of a cube of Jello. If you poke the top surface of the Jello at an angle, the Jello responds in two directions: there is a force straight up that opposes the poking force downwards, and a separate sideways force (the shear force) that opposes the force sideways.
A tensor is used in this case to keep track of the two forces at once: if the poking force is expressed as a tensor it can be divided into separate downwards and sideways displacements, for which forces can be separately calculated, and recombined into a new tensor. The stress tensor (displacement) results in a strain tensor just like stress results in strain in the single vector model, the tensors just do the calculation twice. Normally this is done in 3 dimensions, so stress/strain tensors are both 3 x 3 matrices.
The other common place tensors are used is in magnetism, where the susceptibility thingy is a tensor.
Tensors are required when you start with two directions but the result has to be in a direction out of the plane of the two vectors. With two vectors you can use the cross product to get a vector at right angles out of the common plane, but you can’t get a generalized direction out of the plane.
For that, you need something that represents two vectors simultaneously: a rank 2 tensor.
Give me some feedback: was this a good or bad explanation?
Knowing it took me around two semesters to understand what eigenvalues are actually for, I’d say that’s an excellent explanation. Much better than my professors anyway.
“If one of the vectors is zero length, then the determinant will be zero. This is a degenerate case that isn’t a tensor, so we see from this that a rank 2 (two vectors) tensor can be represented by a matrix, but not all matrices are rank 2 tensors.”
That kinda comes out of nowhere. It’s the first time you use the word “tensor,” and it’s phrased as though the reader is supposed to already understand why that matrix doesn’t represent one. It only makes sense after you already know what it’s supposed to be explaining, just like “A tensor is an object that transforms like a tensor.”
Nice approach thanks, takes me back, looking forward to clarification as per reply/query by bunsen ?
It’s good I’ve read a couple of times now.
I think the only points I think would need to be clarified.
– Why matrixes? Why not just the two vectors?
– why should we use eigenvectors and eigenvalues is that the best way to encode that info?
– what are eigenvectors and eigenvalues anyways?
Otherwise I think it’s a good explanation better than average you’d come across in class in elevator pitch style.
Everyone – thanks for the feedback. This explanation comes from one of my lectures and assumes the students have already studied matrix math, and so have encountered determinants and eigenvectors.
I have a similar explanation for matrices in general that talks about eigenvectors and determinants and such, but it was out of scope.
You never get specific feedback like I’m getting here, and I really appreciate it. It’s actually *hard* to craft a good explanation because you never see what the reader doesn’t know, and never see what you assumed or forgot.
I’ll update my notes per suggestions above and make a better presentation.
It’s not a bad explanation for an engineer Or probably for a physicist, but it’s not the way it’s taught as pure maths, because pure maths is pure.
Maths for engineers is often taught the same as maths for mathmos, because maths is maths, right? Plus you’ve got a big pile of maths textbooks to use. But that’s not necessarily helpful for engineers.
Explanations like this can be helpful from a pure maths perspective, but they can also implicitly cut out other uses of the pure maths, which may be completely unrelated to the ‘simple’ engineering example.
That said, I’m all for teaching them in a pure maths context as long as the ‘pure’ form is also taught. However, sometimes there is no simple explanation or application for a branch of pure maths – or indeed any known application. So if you’re studying pure maths, you do need the capability to handle ‘pure’ concepts or you’ll get stuck.
As an example, chatting with engineer and natural science friends at uni about Fourier transforms showed we had fundamentally different understandings of what FTs were – IIRC with the engineers not actually knowing they were using FFTs not FTs. That’s fine, and it worked for them, because that’s what they were doing with them. And a pure explanation worked for us mathmos, because we didn’t need to know about whatever engineering constraint it was they were using them for, which would probably have taken a term to understand correctly.
For Newtonian physics, physicists like to start with “Assume a three dimension space that is isotropic and homogeneous.” Homogeneous means it has the same properties everywhere, like homogenized milk. Isotropic means it has the same properties in every direction, as opposed to something like a crystal, or a bent piece of iron that is being stretched on the outside of the curve and compressed on the inside edge.
So, how do you work with non-isotropic and non-homogeneous situations (meaning the real world)? Tensors. And that is why they are complicated. To keep it complicated, matrix algebra matches the algebra over some spaces that can describe what we need. This niche of matrix algebra allows manipulating tensors. And in Einsteins index notation, it looks like algebra again.
It is really complicated. “A]n algebraic object that describes a linear mapping from one set of algebraic objects to another.” doesn’t do it justice. There is an algebra over a space defined by the problem. A row space or a column space or a Clifford algebra. That algebra allows objects to transform in a way that matches the real world, at least as far as the components are accurate. But it is complicated, because those components in the matrix are partial differentials. Gilbert Strang’ free MIT lectures on linear algebra are a great resource.
But also kids don’t pay attention and are still developing and may not have the aptitude to pick it up yet. There is always a balance with teaching early to allow kids with potential to start on time and late enough that every kid meets some minimum mental age to take in the info.
Finally, they probably pick it up quicker because they remember the old techniques and cryptnesia (?sp) means insights they suddenly have where things they were taught years ago! This is after all how revision works.
Some people lagging is never a reason to hold back those that don’t. You’ll need to address both, but don’t sacrifice one for the other.
That’s why schools use streaming although it’s always been controversial.
When I was at school core classes were split into three (A- too set, B, C- bottom set) plus generic “gifted” clubs and remedial clubs.
Not including SEN (special educational needs ) classes.
Still in a believer that schools who provide a good education but can’t and shouldn’t be expected to provide an education that could rival say private tuition which is what the very best would benefit from.
Butchered that last bit beyond recognition.
Schools should provide a good education, but can’t be expected to do it all. Tuition still required (might just be your dad giving you a hand with some physics).
Streaming is controversial because it classified children as ‘bright’ vs ‘thick’, and groups them academically and socially by this, which can re-enforce lack of self-confidence.
In the U.K. most schools use setting, which is a per-subject split. So kids can be in different sets for maths vs English. And they usually reset every term (=3x per year), so it’s not a ‘permanent’ assignment.
Unfortunately most schools only set on ‘academic’ subjects, which must hella-ffrustrate the kids who are good at sport when they’re made to play with geeks, and also reenforces a “sport is not for geeks” attitude, when actually we can enjoy it if we’re not playing against a class full of Renaldos.
Hmm, fascinating, this might tickle a thought, just added this moments before this hackaday article:-
https://www.quora.com/If-you-hold-the-strongest-rare-earth-magnets-of-same-poles-together-leaving-a-small-gap-what-properties-does-that-space-have-such-as-energy-tension-and-are-any-useful
Tenser, said the Tensor http://wiki.c2.com/?TenserSaidTheTensor
“Einstien”? Really?
The video was just annoying.
Well, maybe not “just”, but it certainly was annoying.
Are you being “just” in your assessment?
B^)
There’s quite a few videos on Youtube explaining Tensors.
Continuum mechanics and mechanical engineering use tensors a lot. Just part of the game in stress analysis and fluid mechanics. Yield surfaces, deviatoric stress vs. hydrostatic stress (look that one up) – all fun stuff.
Learned all about tensor math in college for electronics. Never used it in practice…
anything above algebra is “spicy math”
I was told numerous times that I would need to know Calculus to advance from my lowly Cobol Business programmer job back in the 70’s to become an Engineering programmer. I looked at some books and could not make heads or tails of it, but then found “Calculus Made Easy” by Silvanus P. Thompson, a 1919 book by a Victorian era scientist that made everything clear after I spent a few months working through it. The book is still in print or obtainable from archives.org.
After taking some EE math courses at Univ. of Rhode Island, I got the first of several engineering/communications software jobs and a big jump in pay. But in 32 years of software work, I never needed to know or use Calculus. Algebra yes, Calculus no.
Years later I saw a book about Einstein and his use of Tensors but was older and wiser then and left that to the physicists. Perhaps now, I will take a look at this interesting branch of math now that I’m retired.
Thanks !
Math is a HARD subject BECAUSE something that makes sense to you and you can explain it takes a different pathway to understand it.
So just understanding the explanation doesn’t work unless you can break up those building blocks and use the appropriate step use those “tools” to rebuild that pathway.
Speak up in math class and explain it back the shame of saying it wrong is worse then getting it wrong.
Sorry most professors are pretty shitty at explaining things. A craftsman trade professional who works as an instructor does a must much better job.
P.s. great video
Awesome video! really helped me understand why tensors are important for geophysical calculations.
Can you do more that apply to geophyscists? lots of us know about rocks, but are lacking in the math and physics areas.