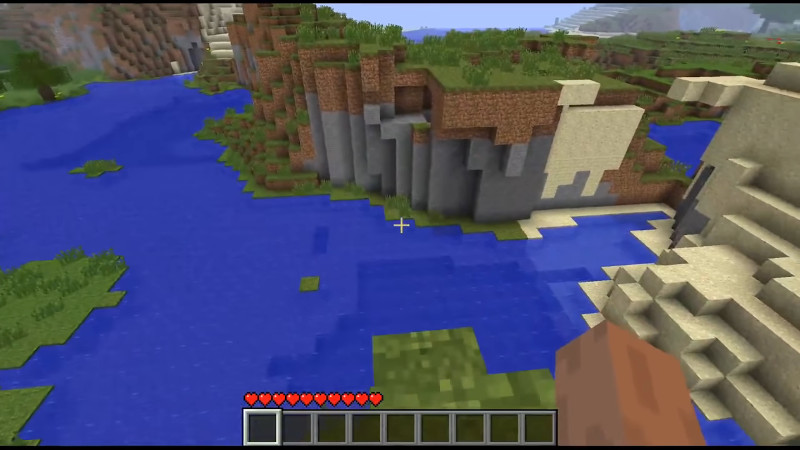
Minecraft is a game about exploring procedure-generated worlds. Each world is generated from a particular “seed” value, and sharing this seed value allows others to generate the same world in their own game. Recently, the distributed computing project Minecraft@Home set about trying to find the seed value of the world shown in the Minecraft title screen, and have succeeded in their goal.
The amount of work required to complete this task should not be underestimated. 137 users contributed 181 hosts with 231 GPUs to the effort, finding a solution in under 24 hours. The list of contributors to the project is a long one. It appears the method to find the seed involved comparing screenshots from various seed worlds to the original image. This took a lot of reverse engineering in order to calculate the camera FOV and other settings of the original capture, such that the results could be compared accurately. Interestingly, the group found two seeds that can generate the requisite world, suggesting the world generator code has some collisions between seed values.
We’re not sure what’s more astounding, the amount of work that went into the project, or that there’s a distributed computing project tackling advanced Minecraft research. Either way, we’re no strangers to Minecraft hacks around these parts. Video after the break.
















> Interestingly, the group found two seeds that can generate the requisite world, suggesting the world generator code has some collisions between seed values.
Can someone with the necessary experience weigh in here? My thoughts are below.
My gut says that this should not be that surprising. I’m thinking of random systems where the internal state space is much bigger than the entropy possible for the seed. Or would it be more precise to say the intended state space is much larger than the internal state space of the generator.
Famous example of this is using the Fisher-Yates shuffle for a deck of cards (https://en.wikipedia.org/wiki/Fisher%E2%80%93Yates_shuffle#Pseudorandom_generators) the intended state space of a deck of cards is 52! which is over 225 bits. But most random modules will wont supply this.
Python 2.7 looks to be a case in point (https://github.com/python/cpython/blob/2.7/Lib/random.py#L32) uses MT19937 (https://en.wikipedia.org/wiki/Mersenne_Twister) which provides only 32 bits!
The possible or intended state space of Minecraft maps is probably humongous, while the random generator likely has a much smaller state space.
I re-read this and don’t think I explained my self well
https://imgur.com/a/eWn481F
Maybe this will help.
So the question isn’t will there be collisions (of course there will be) but how likely are they?
Notice the PRNG (typoed as PRN) state space is SMALLER than the seed space, and much smaller than the possible states of the output so only a tiny subset of it is utilized.
Then seed space (in bits) / internal PRNG space (in bits) = collision rate?
It’s more a form of the reverse. There are many intermediate values used as seeds for different parts of world gen. “World seed” tends to mean the top/main value when one doesn’t say otherwise.
All the other intermediate stages take a smaller number of bits out of that world seed, which have values of lesser bit counts taken from them, and so on.
You can think of it as generating 48 bits from the pRNG, then taking 8 of those bits for the terrain height map, then taking 7 bits from the height map to use for the biome map.
There will be two 7-bit values that match within the higher 8-bit value, so two different seeds that generate identical biome maps but different terrain maps on top of it.
There are even certain intermediate stages that are much much smaller, and ways to intentionally pick a seed such that two values out of it repeat in a predictable pattern, for instance always 16 off from each other. 16 being a chunk size (well, 16×16 blocks, but still)
In the code there are plenty of opportunities where they could have added in more bit shuffling or hashing or such to make such events more rare or harder to intentionally setup, but remember this isn’t crypto, it’s a game. Not only is there no need at all for that, but it can be quite fun in itself toying with these values, and ultimately fun is the entire point, no?
Very enlightening thanks for the thorough reply
Interesting details. If you convert those two seeds to binary:
001110111011101000101110000111111100011111001010000110111101001
111000001001100000101110000111111100011111001010000110111101001
The first 15 bits differ
001110111011101 vs 111000001001100
but the others are identical. I don’t have Minecraft to play with, but maybe someone could try some other options for the first 15 bits and see if all the worlds look the same in that area?
Just yesterday I was introduced to the concept of “shadow seed” in Minecraft.
https://www.youtube.com/watch?v=ybqWm6sRdeY
This has been done successfully in the past to find PewdiePie’s seed, among other things, to figure out whether or not his dog should in fact have drowned in the ocean.
https://www.youtube.com/watch?v=g7DmvkvONH0
Dream inspired me to start play minecraft himself, but he’s going at it with an engineer’s mindset, which is absolutely amazing.
I’m always happy to see “137” in a HaD article, it’s one of my favorite numbers on its own but of course the fine-structure constant α ≈ 1/137.
Collisions between seed values or just that the stuff in view of the camera is the same?
That is exactly what they mean but don’t want to admit.
They have not found the seed world, they found one that matches the handful of title screen pictures. Add up all the blocks and you have what maybe 5000 random blocks to select. Of those blocks there are maybe 10 unique blocks each one could be so they need to hit 50k random numbers. While a large number it sure isn’t when you are churning through all possible random seeds. I bet anything there are hundreds of collisions for the requierments they set, it just really seems pointless.
No, you are completely wrong. They found THE SEED. It is not that they don’t want to admit it. It is just the implementation of Java random has collisions. Every seed has 65536 copies of itself. Only a handful is possible naturally. You can actually do this experiment yourself:
Experiment:
1. Go back to the version they are talking about, version BETA 1.7.3.
2. Make a world with the seed 1. And explore a little. Save the coordinates!
3. Now make a world with the seed 281474976710657. Now go to the same coordinates as before.
These two worlds are exactly the same.
Java random has collisions therefore there are two seeds with the same world.
That’s what I also thought. It’s like looking at 8 bits of a 64 bit PRPG. Many states the PRPG takes on will have the same values in those 8 bits. 2^56 states to be precise.