In the last decades, our understanding of the Universe has made tremendous progress. Not long ago, “precision astronomy” was thought to be an oxymoron. Nowadays, satellite experiments and powerful telescopes on earth were able to measure the properties of our Universe with astonishing precision. For example, we know the age of the Universe with an uncertainty of merely 0.3%, and even though we still do not know the origin of Dark Matter or Dark Energy we have determined their abundance with a precision of better than 1%.
There is, however, one value that astronomers have difficulty in pinning down: how fast our universe is expanding. Or, more precisely, astronomers have used multiple methods of estimating the Hubble constant, and the different methods are converging quite tightly on two different values! This clearly can’t be true, but nobody has yet figured out how to reconcile the results, and further observations have only improved the precision, deepening the conflict. It’s likely that we’ll need either new astronomy or new physics to solve this puzzle.
The Discovery of the Expanding Universe
In the 1920s Edwin Hubble used the newly built telescope at Mount Wilson Observatory to study fuzzy objects known as nebulae. Back then, astronomers were arguing whether these nebulae are clouds of stars within our Milky Way or if they are whole different galaxies. Hubble discovered stars within these nebulae whose brightness slowly fades in and out. These were known as Cepheids and previously studied by Henrietta Levitt who showed that there was a tight relationship between the star’s intrinsic brightness and the period of its variation. This means Cepheids could be used as so-called standard candles which refers to objects whose absolute brightness is known. Since there is a simple relationship between how the brightness of an object decreases with distance, Hubble was able to calculate the distance of the Cepheids by comparing their apparent and intrinsic brightness. He showed that the Cepheid stars were not located within our galaxy and that nebulae are actually distant galaxies.
Hubble also measured the velocity at which these distant galaxies are moving away from us by observing the redshifts of spectral lines caused by the Doppler effect. He found that the further away the galaxy is located, the faster it is moving away from us described by a simple linear relationship.
The parameter H0 is what is known as the Hubble constant. Later the Belgian priest and physicist Georges Lemaître realized that the velocity-distance relationship measured by Hubble was evidence for the expansion of the Universe. Since the expansion of space itself causes other galaxies to move away from us we are not in any privileged location but the same effect would be measured from any other place in the Universe. An effect that is sometimes illustrated by drawing points on a balloon, when it is inflated the points move away from each other at a speed that depends on their distance. It is also better not to think of the cosmological redshift as being caused by a real velocity as the parameter v in the above equation can easily exceed the speed of light.
Since astronomic distances are commonly measured in Megaparsec (Mpc), which is equal to 3.26 million light-years, the Hubble constant is expressed in (km/s)/Mpc. The value of H0 is about 70 (km/s)/Mpc which can also be expressed as 7%/Gyr, meaning that the distance between two objects will increase by 7% after a billion years.
The Hubble Constant is Not Constant
Even though we speak of the Hubble constant it is a bit of a misnomer since its value is changing over time. We call this the Hubble parameter H(t) while H0 is simply the value of H(t) today. We now know that the expansion of the Universe is accelerating, so what does this mean for the Hubble constant? One might think that it will get bigger but actually it is decreasing, which can be shown with a little bit of math. We can express the Hubble parameter using the distance between two points and its time derivative
:
If we have an accelerated expansion , we get
and thus
. This means H(t) is decreasing with time. The velocity of any galaxy will increase over time because it is further away. If we look at a fixed distance, however, the velocities of different galaxies that will pass by this point will decrease over time.
How do we actually know that we live in an accelerating Universe? The proof for this came from the measurement of the redshift of distant supernovae made in the late 1990s. Similar to Cepheids, supernovae of Type 1a can be used as standard candles (i.e. their distance can be derived from their apparent brightness). Since exploding stars are generally very bright objects they can be seen from very far away.
Looking at very distant supernovae also means looking far into the past, so when the Hubble constant is changing it will have had a different value when the light from that supernovae started traveling towards us. When plotting the distance vs the redshift of supernovae one will thus see a deviation from the linear relation of the Hubble–Lemaître law for high redshifts. In the 1990s, astronomers expected to see evidence for a decelerating Universe as they thought the expansion should be slowed down due to the gravitational pull exerted by matter. Surprisingly, they found an accelerated expansion which was evidence for another form of matter or energy that acts repulsively.
Einstein originally introduced such a force to his equations of General Relativity known as the cosmological constant, denoted by the Greek letter Λ (Lambda). Ironically, it was introduced to generate a static Universe so Einstein abandoned the idea (“my biggest blunder“) when Hubble discovered the expansion of the Universe. Later the term Dark Energy was coined for the force that drives the accelerated expansion.
The Echo of the Big Bang
How do we tell how far away other stars are anyway? Astronomers have constructed a cosmic distance ladder that successively increases distance measurements using different methods. At the base of the ladder are nearby stars whose distance can be directly determined through measurements of the parallax — the apparent shift of an object’s position due to a change in an observer’s point of view. This measurement can then be used to calibrate the distance of Cepheids which then are used to calibrate the distance to Type 1a supernovae, which have brightnesses that depend on other physical properties.
Besides the distance ladder measurements described above, there are also other ways to determine the Hubble constant. One of the most precise measurements of the properties of our Universe comes from the observation of the cosmic microwave background radiation (CMB). The CMB was accidentally discovered by the radio-astronomers Penzias and Wilson after they ruled out that the signal they saw was caused by pigeons nesting in their antenna. This omnipresent source of electromagnetic radiation that peaks in the microwave region was created about 380,000 years after the Big Bang. Before that, the Universe was an opaque plasma as light did constantly bounce off free electrons and protons. Once the plasma had cooled down to about 3000K, electrons combined with protons to form neutral hydrogen atoms and light could travel freely thus the Universe became transparent.
This light which has been redshifted due to the expansion of the Universe can now be observed as the CMB. Since CMB photons are moving freely after they were last scattered they contain a snapshot of the Universe as it looked 380,000 years after the Big Bang. Through measurements of the CMB and the comparison with cosmological models, it is thus possible to extract important parameters like the aforementioned amount of Dark Matter and Dark Energy, or the Hubble constant.
Is the Universe Expanding Faster Than It Should?
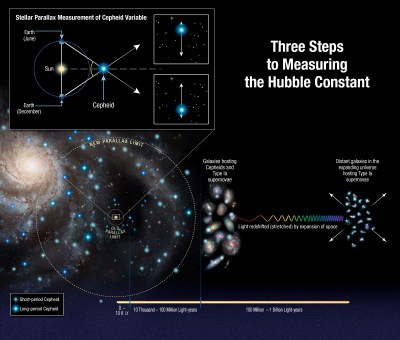
Credit: NASA, ESA, A. Feild (STScI), and A. Riess (STScI/JHU), CC BY 4.0
Currently, the most precise measurement of the CMB was performed by the Planck satellite. Its observation agrees with the current cosmological standard model, the ΛCDM model, where Λ stands for Dark Energy in form of the cosmological constant and CDM for Cold Dark Matter. The Hubble constant derived from the Planck measurement is H0 = (67.4 ± 0.5) km/s/Mpc.
However, distance ladder measurements give a value that is about 10% higher. The most precise value, in this case, was derived by the SH0ES team which used the known distance of nearby Cepheids in the Milky Way and Large Magellanic Cloud to calibrate the distance of extragalactic Type 1a supernovae as illustrated in the picture. Compared to the Planck measurement they arrive at a significantly higher value of H0 = (74.03 ± 1.42) km/s/Mpc. The tension between these two values is 4.4 standard deviations which corresponds to a probability of <0.001% as being due to chance.
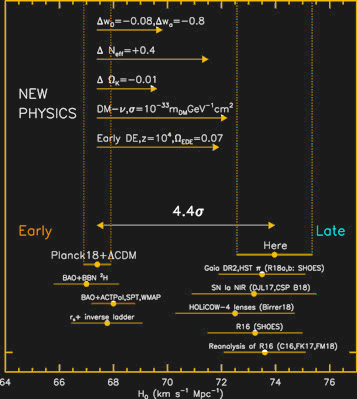
Credit: A. G. Riess, et al.
Of course, many people have tried to pin this discrepancy down to any unaccounted errors in either of the experiments but without success. Also, the discrepancy is not only between these two experiments but there are other distance ladder measurements that all point to a higher value of H0.
Making the whole situation even stranger, the CMB measurement by Planck has recently been confirmed by the Atacama Cosmology Telescope which measured a Hubble constant that is consistent with Planck’s value. In addition, CMB measurements are backed by observations of so-called baryon acoustic oscillations (BAO) combined with other astronomical data. In general, one can observe the trend that the values of H0 derived from the early Universe (CMB, BAO) are lower than those from the distance ladder measurements which use objects with much lower redshift and thus capture a more recent state of the Universe.
An important point is that the CMB measurement is model-dependent meaning that H0 is derived under the assumption that the ΛCDM model describes our Universe. So an exciting explanation for the discrepancy would be new physics beyond the current cosmological standard model. Among the many new physics interpretations for the H0 discrepancy is the idea that Dark Energy is not simply a constant but also time-dependent. Other theories include interacting Dark Matter or new relativistic particles. However, as can be seen in the figure none of these ideas can completely resolve the Hubble tension.
New Techniques to Measure Cosmic Expansion
Other techniques for determining the Hubble constant include the measurement of gravitational-lensing time delays. Strong gravitational lenses can create multiple images of an object located behind them. Since the images have different light paths there is also a time delay at which these images arrive which can be measured when the object varies in brightness. By modeling the gravitational potential of the lens and knowing the redshift of both the lens and the source, it is possible to extract the Hubble constant from this time-delay measurement. The H0LICOW (H0 Lenses in COSMOGRAIL’s Wellspring –astrophysicists have a weakness for wacky acronyms) collaboration has recently used this method to determine the Hubble constant, and their value is consistent with the distance ladder measurements and in tension with the CMB result.
In the future, completely independent measurements of the Hubble constant may shed more light on this mystery. One of them is the use of gravitational waves “standard sirens”. In this case, the absolute distance can be directly determined from the gravitational-wave measurement while the redshift is determined from simultaneous observation of electromagnetic radiation. The advantage of using gravitational waves is that the absolute distance of the source can be directly determined without any intermediate distance measurements. So any systematic error that we might have in the cosmic distance ladder will not influence the result.
The method was used to extract the Hubble constant from the gravitational-wave events GW170817 and GW190521, however, due to the large error bars, the results are consistent with both CMB and distance ladder measurements. Fortunately, the uncertainty will shrink as more and more gravitational-wave events are detected and so we will likely be able to tip the favor for either the high or low H0 value in coming years.
On the one hand, the Hubble tension is an annoying inconsistency in our otherwise well-confirmed understanding of the Universe. On the other hand, it might be an exciting glimpse of new physics. So let’s keep the hopes up that future observations will solve this puzzle and lead to new revelations.
















What we can see is expanding. It’s expanding into other parts of the universe.
This is THE most common fallacy regarding how ‘the universe’ is thought of; of how difficult it is to even imagine; to, at bottom, even comprehend the concept of occupying some ‘place’ which is not a part of some ‘larger place’.
‘The Universe” is NOT expanding inTO ANYTHING ELSE. There IS no ‘anything else’. All that exists consists of a universe which is continually getting larger–but it is NOT expanding “…into something else…”.
‘The universe’ is all there is. Period. There is NOTHING outside ‘The Universe’.
As Einstein put it–
“Once you can accept the universe as matter expanding into nothing that is something, wearing stripes with plaid comes easy.”
–Albert Einstein
“The universe is not only stranger than we imagine, but it is stranger than we can imagine.”
–JBS Haldane
“There is a theory which states that if ever anyone discovers exactly what the Universe is for and why it is here, it will instantly disappear and be replaced by something even more bizarre and inexplicable. There is another theory which states that this has already happened.”–Douglas Adams
The universe is both infinite AND expanding at the same time. And no, it’s not expanding into other parts. It’s like Hilbert’s infinite hotel conundrum.
You have a hotel with an infinite number of rooms, numbered 1, 2, 3, etc. They are all currently full. An infinite number of people come into town for a convention and need rooms to stay in. But you’re full up. Or ARE you? You take the person in room 1 and move them to room 2. You move the person from room 2 to room 4. Move the person in 3 to 6, etc. Now you have all of the odd-numbered rooms empty and there’s an infinite number of them. So you check in all the new-comers.
You didn’t move part of the hotel to other parts that were empty (it’s full, remember?) You didn’t make a bigger hotel (it’s already infinitely big.) But you still managed to expand the number of guests that you are accommodating.
Better stated as “the Universe *can be* infinite and expanding at the same time.” The problem is the definition of the Universe. Our *observable* Universe (everything from us to the particle horizon) is clearly finite, and expanding. But we’re pretty sure the Universe must be *dramatically* larger than just our observable Universe, because even things out to our particle horizon look uniform. So the presumption is that those galaxies, at present time (which we can’t actually observe, and at far distances, never will be able to!) see a similar volume of the Universe, mostly distinct from ours, and that Universe is (statistically) identical to this one.
But the problem is that if you try to extrapolate that *again*, we don’t have any real anchor for that, at all, because we (currently!) have no information (and our ‘best information’ there will likely come at the particle physics level, eventually).
It’s like asking an ant – the last ant ever, with a finite lifespan, on a planet the size of the Milky Way galaxy if the planet is finite. The finite and infinite versions are completely indistinguishable to him. The *concept* of the Universe may be interesting to the ant, but he’s completely incapable of discovering it, so does it make sense for him to even think about it?
But like I said, the problem is in the definition of the Universe. Encompassing it to “everything” turns it into a massive extrapolation. (This is a restatement of the answer to the “flatness problem” – “why is the Universe so nearly flat?” The common answer is “inflation”, but that implies that the Universe *may* have had a pre-inflation curvature which is now unknowable).
“The universe is both infinite…”
Wrong. If the universe were infinite, it would not have an age of approximately 13.7 billion years; an “infinite universe” would have to have been infinite forever.
An ‘infinite universe’ corresponds precisely to the Steady State Universe [SSU] as postulated by Hoyle, Gold, and Biondi, whose conjecture ONLY and SIMPLY requires that matter and energy be continually created out of absolutely nothing. Other than this trivially unimportant fact, there’s nothing at all wrong with the Steady State Universe theory.
The gentleman responsible for the ‘Big Bang’ Theory was Georges Lemaître, who proposed Hubble’s Constant two years before Hubble; and who posited the ‘Big Bang’ Theory by simply working backwards to the unassailable conclusion (origin?), which he called the origin of the universe; and formally calling it the “hypothesis of the primeval atom”.
By the way, Hubble’s Law is now officially known as the Hubble–Lemaître law by the IAU (International Astronomical Union).
The death knell of the SSU was provided by the formal discovery of the CBR, or CMBR, by Penzias and Wilson, of Bell Labs, in 1965. The value of (approx) 2.5K is in excellent agreement with the time-value extrapolated from an exceedingly hot initial ‘big bang’.
By the way, the term ‘Big Bang’ was a pejorative term–meant to be “snarky”– disparagingly assigned by Hoyle, who–along with his associates–found Lemaître’s views–and conclusions–distasteful enough to propose an alternative “theory”–which he (Hoyle) adamantly pushed for a very long time…until he couldn’t any longer.
The universe can be infinite in size (which was what I meant) without it being infinite in age/time. But Pat did have a good point in that I should have said “might be.”
It’s also worth noting that when we say “the Universe has an age of X” we actually mean “the Universe’s expansion, projected backwards, reduces to a point at time X.” We know the CMB occurs at a redshift of z~1100, corresponding to ~300kyr after that point, and we also know that Big Bang nucleosynthesis is *remarkably* accurate, implying that nothing weird was happening from t~O(10-1000) seconds to the CMB formation. But that first t=0 to t~10 seconds is unanchored experimentally at the moment. Discovery of inflation would get us to essentially the moment of the Big Bang, but before that is particle physics-land.
So even saying “the Universe is finite in time” is sketchy. It certainly seems like it is, but it’s worth remembering what that means! If the Universe is finite in time, that implies violation of energy conservation : that’s Noether’s theorem. We cheat, and bury that energy conservation in an inflaton field, but when people propose theories to *explain* that violation, unsurprisingly you usually end up erasing/extending the t=0 singularity and making the Universe infinite again. But without any *evidence*, getting rid of that t=0 singularity is just a physicist imposing his *preference* on the Universe.
In other words : saying things about the Universe as a whole is super-ultra-mega tricky, because we just don’t have any information, and in fact we might *never* have any.
One must be very careful about violating ‘Feynman’s Dictum’ (“…just let them keep talking…”) regarding how to determine the level of expertise–or not–of one who holds forth, with authority, on any subject.
For all the great minds (as well as some not-so-great) who have weighed in on Lemaître’s “primeval atom” postulate (theorem, now) over the years, not one has ever invoked, or appealed to the authority of, Noether’s Theorem, which was created many, many years before Lemaître…with good reason: it simply does not apply. If there were ever a good case for using ‘Noether’s Theorem’ as ammunition against the Big Bang Theory, the infamous ‘gang of three’ (Hoyle, et al) was it. But they demurred. And the silence was deafening.
The mathematics, and even the philosophy and physics of Noether’s Theorem–in no way, shape, or form–apply to any consideration of the ‘Big Bang’ theory.
No, it really does. I think you’re misunderstanding what I’m saying though. I’m not using this as “ammo” against the Big Bang, f’crying out loud. Far from it. I’m using it as ammo against people who claim that getting rid of the t=0 is *a feature* of some random theory they come up with (Which is common).
Noether’s theorem connects a conserved current (in this case, 4-momentum, or specifically the timelike component, energy) to an action symmetry (in the case of energy, time). That’s like, upper-level undergrad. No big deal. In order for the action to conserve energy, it can’t have a global time dependence.
Then, of course, you ask “wait, how does that work with cosmology, cuz it’s certainly got a global time dependence” and the answer is “it doesn’t.” Cosmology is *observational*, and if we just look at our universe, with the physics that we currently know, *as it is*, energy isn’t conserved. Duh. So what? We don’t understand the physics that gives us the Universe we have in the first place!
My comment might’ve been a bit “esoteric theoretical vs experimental physicist” but let me be clear, it’s really straightforward – if you try to *explain* the “global timescales” via some theory that requires a time-invariant action you’ll end up getting rid of those global times… cuz the theory’s time-invariant. However, strangely, this fairly self-evident point seems to surprise lots of theorists, and they say “hey look, in my theory, there’s no t=0 singularity” as if this is some unique thing.
And, incidentally, this isn’t just me saying this:
https://www.preposterousuniverse.com/blog/2010/02/22/energy-is-not-conserved/
“The point is pretty simple: back when you thought energy was conserved, there was a reason why you thought that, namely time-translation invariance. A fancy way of saying “the background on which particles and forces evolve, as well as the dynamical rules governing their motions, are fixed, not changing with time.” But in general relativity that’s simply no longer true. Einstein tells us that space and time are dynamical, and in particular that they can evolve with time. When the space through which particles move is changing, the total energy of those particles is not conserved.”
Huh. Conservation of energy = time-translation invariance. Which theorem connects those again?
Now, it is readily apparent that you are dodging the issue, and engaging strictly in personal opinion.
I’ll say it again, in hopes that it gets through this time:
“For all the great minds (as well as some not-so-great) who have weighed in on Lemaître’s “primeval atom” postulate (theorem, now) over the years, NOT ONE has ever invoked, or appealed to the authority of, Noether’s Theorem, which was created many, many years before Lemaître”
Now here’s the very crucial point: NOT ONE.
Not Eddington; not Einstein; not anyone at any of the Solvay conferences; not even–and mark this VERY well–Georges Lemaître, himself.
ALL these people were outstanding physicists and mathematicians, and all certainly well aware of Noether’s work.
The answer is very simple: to state that Noether’s Theorem has anything to do with, or impacts in any way, the scientific explanation of the origin of the universe is simply a red herring; it is–again–simply wrong**. This ‘appeal’ to Noether’s Theorem in your ‘exposition’ comprises a complete and total lack of logical consistency and rational necessity, and adds absolutely nothing to the dialogue.
[**One cannot help but be reminded of the famous one-liner of Wolfgang Pauli: “It is not even wrong.”]
*****************************************************************************
“…In other words : saying things about the Universe as a whole is super-ultra-mega tricky, because we just don’t have any information, and in fact we might *never* have any.”
It’s always a delight to have things explained scientifically.
“We need to teach how doubt is not to be feared but welcomed. It’s OK to say, “I don’t know.” –Richard P. Feynman
I think you actually think I’m making the *exact opposite* point that I’m making.
“The answer is very simple: to state that Noether’s Theorem has anything to do with, or impacts in any way, the scientific explanation of the origin of the universe is simply a red herring”
Noether’s theorem is just a connection between action symmetries and conserved currents. That’s it. OK?
Applying it to conservation of energy gives you time-translation symmetry.
*Many* theorists (— not me —) believe that if they “fix” physics to explain dark energy/inflation/god knows what else and they *end up with* a time-symmetric universe, that’s an indication that they’re *right*. *That* is what I’m saying is wrong. That is – appealing to conservation of energy via Noether’s theorem as a justification for getting rid of the Big Bang *is not an improvement in and of itself*.
Which, I think is *exactly the same thing* as what you’re saying.
And if you think *no one* brings this point up, you’ve not *nearly* sat through enough string theory/quantum gravity talks… or maybe it means I’ve sat through too many (that’s probably true anyway). Or maybe you’re having the same visceral reaction I have when someone thinks classical conservation of energy is like, “a thing” for the Universe as a whole.
I mean, this entire point started because I said if you have a finite-in-time Universe, you don’t have time translation symmetry, implying lack of energy conservation (in the *classical* sense – maybe that was the part that was missing?). That bothers the *hell* out of some people, so they try to “fix it.”
I don’t *agree* with any of that, I think it’s hilarious.
“It’s always a delight to have things explained scientifically.”
Weird, I didn’t realize this was a scientific conference.
It’s worth noting that a lot of the difficulty is because the time gap between “early” and “late” is… unobservable. You’ve got this massively obvious observable in the Cosmic Microwave Background, which dates to the point at which the Universe cooled enough for atoms to form : but at that point, the Universe was just this big freaking ball of hot hydrogen that expanded. That was about ~400K years after the Big Bang.
But from that point until something like *at least* 150M years later, the Universe was just… there. Nothing was hot enough to glow, but nothing had gotten *cold* enough to start condensing, so it’s just… dark. There’s a brief period after the CMB formation where the gas was glowing due to being excited by the CMB (until about 3M years), but then things cooled enough that basically *nothing* was glowing. No light. Nothing to observe. Astronomers call this the “dark ages” and they really mean it. From 3M to at least 150M years afterwards, there’s just… nothing to see. And that 400K->3M ‘glow’ is going to be essentially unobservable, as it’s equivalent something below 10 MHz radio now, and, uh, there’s *just a bit* of noise there from other stuff (the galaxy is wacko-noisy at low frequencies).
At 150M years, the Universe starts to light up again due to stars forming, and we *might* be able to see hints of the Universe glowing in that first light (which is around ~100 MHz now), which is what the LOFAR observatory is hoping for. But again, gee, I can’t think of *anything* that would cause problems around 100-200 MHz.
Those measurements would *really* provide a totally new anchor for Hubble measurements, because it’s finally in a new time period. Even then, though, it still leaves a completely dark period of the early Universe where you just have no idea how the hell things expanded – and sadly, likely never will.
Thank you for the clear comment!
For all we know “the Universe” is only a spec in an infinitely larger universe in both space and time. Basically we know nothing.
No, we pretty much *do* know that it is!
It’s a common misconception that when people talk about the “size of the Universe” they’re thinking astronomers mean “the whole Universe.” They mean “the *observable* Universe” or even more specifically, the “Universe observable by light.” So you’ll say something like “oh, right after the Big Bang, the Universe was the size of our Solar System” or something like that. But what they mean is right after the Big Bang, *everything you currently can see* was the size of our Solar System.
But they’re not saying that, for instance, if you find a way to travel faster than the speed of light, that you would *ever* run into “the end of the Universe.” There’s no evidence that the Universe is, or ever *has* been, anything other than infinite. Certainly *our* observable Universe is not the same as the observable Universe of someone 11 billion light years away. It’s just that patches that started out “small” (like the Solar System) are now massively bigger, and still expanding.
Like I said, this is a really common misunderstanding. The Big Bang doesn’t mean the *whole Universe* started as a point. It means *our observable Universe* – like, Earth’s observable universe – started as a point. We *know* there’s more than our observable Universe, though. We just don’t know how much, and without faster-than-light stuff, we’ll never know: because we’re pretty sure the *Universe itself* expanded *much, much faster* than the speed of light, originally.
It’s yes and no at the same time. According to Steven Hawking in the book “A brief history of time”, time itself changes in the presence of a big mass. One interesting thing to look at is gravitational time dilation (caution, it might make your head explode) https://en.wikipedia.org/wiki/Gravitational_time_dilation
It says that closer to big bodies of mass the time elapses slower. Further away from mass it goes faster. Without mass there’s no concept of time. Hawkings says there is a boundary to our universe, it’s not just the edge of what we can observe. There’s no physical way to get past the boundary.
On the other hand though, there’s nothing to say that there isn’t another “blob” of mass somewhere where time also exists. Or many more, or infinitely more. There’s just no way to get there as time and space aren’t linked to them. Does your head hurt already? ;-) “A brief history of time” is by far the most impressive book I’ve ever read, I would highly recommend that book to anyone who has a basic understanding of thermodynamics.
Hawking’s welcome to his opinion, and he certainly had plenty. But without more data and understanding of the inflationary period (including, y’know, whether or not it *exists*), there’s absolutely no way to know anything about the structure of the non-observable Universe *as a whole* – whether it’s finite, or infinite, or anything else.
> There’s no evidence that the Universe is, or ever *has* been, anything other than infinite.
There’s no evidence that it is infinite either. The universe is isotropic and homogenous at every scale we’ve measured so far. That tells us nothing about its extent or whether it has any boundaries. The universe being infinite is conjecture at best.
Furthermore, there are plenty of reasons to be skeptical of the infinity of space. Every time physical quantities are unbounded from above or below, we consider them unphysical because it leads to paradoxes. This is also how we know that GR is technically incorrect (singularities).
The actual existence of countable infinity is even a subject of debate among mathematicians, and since physical models are mathematical, that should tell you something about the alleged infinite extent of spacetime.
Yeah, I thought that was obvious (no evidence it’s not finite – no evidence *period*). Observations of the *visible* Universe don’t matter though: this is talking about regions *outside* the initial causal patch that inflated. We have no information about that region : just ideas.
As for the mathematical argument, again, without knowing anything about that region, saying “X is unbounded” is naive. Infinite series are unbounded, but many converge to finite values. You’re literally talking about regions where the laws of physics could be quite different, as inflation happened before symmetry breaking.
An interesting corollary to the “visible universe” is that I really AM the center of the universe – my “visible universe”, that is – as the distance I can observe is exactly the same in all directions from me. YOU are the center of YOUR visible universe, as well (and even your feet exist in a slightly different universe than your head.)
But also it means that, in at least that one respect, there really can be said to be one fixed point that all motion is relative to (it’s just that the one fixed point is relative to the observer.)
Pardon me for being so dense, but if looking further away is looking further into the past, and when looking further into the past we see the expansion increasing, does that not equate to coming back more to the present, the expansion is decreasing, as would be expected. What am I missing?
It’s not exactly like looking further into the past. Imagine it like this. Suppose you find a wheel from 100 years ago that’s been in continuous use. Looking at the wheel is like looking in the past – you see the materials, construction methods, etc. that were all used 100 years ago.
But you can also look at the wear on the wheel, and that tells you about the roads and how they’ve changed *over the entire past 100 years*. Looking at the wear isn’t like looking at the past – it’s looking at the entire history of the wheel.
Same thing here. The *image* of a galaxy 100Mly away tells you what the galaxy looked like 100M years ago. But looking at the velocity shift – the redshift – tells you how the universe changed over that *entire time*. And that’s what’s going on here: we see that over short timescales, the expansion looks constant, but that’s just because the acceleration’s small. Over *long* timescales – using the “oldest wheels” – we can see that the expansion must be accelerating.
Still trying to get my head around this. So is it true that the redshift of objects 50Mly away is increasing at a faster rate than objects 100Mly away, and at a much more faster rate than objects 500Mly away? Is that what you are saying?
Perhaps we shouldn’t know such marvels, seems to me to be a big, shiny red button that shouldn’t be pushed. Problem is, someone will inevitably push it.
For the french-speaking people reading this: this episode of the radio show “La méthode scientifique” is dedicated to this subject, and really enjoyable to listen to!
https://www.franceculture.fr/emissions/la-methode-scientifique/la-methode-scientifique-emission-du-mardi-16-mars-2021
Dark Matter and Dark Energy don’t exist. They’re just placeholders for stuff that is not understood. Not actually things.
basicly yes. I also wonder if the redshift is possible by anything but motion (for example plasma, dust clouds etc.). And what about blueshifts, how can 2 object near each other have blue & red shifts.
It can! You actually can reformulate a lot of cosmology by letting fundamental constants of the universe vary with time, rather than having space be expanding. The net result ends up being exactly the same, however, making the difference essentially solely how you choose to view things. See C. Wetterich, arXiv:1303.6878.
“And what about blueshifts, how can 2 object near each other have blue & red shifts.”
*Relative* blueshifts, not absolute blueshifts. As in, two objects orbiting each other. The line from one’s blueshifted relative to the redshift expected from distance, and the line from the other’s redshifted relative to that expectation.
I’ve been investigating a few different areas of physics for a little over a decade, I’ve been working on hypothesis on over the last few years, originally centred on entanglement, if it turns out to be correct, it has implications for several fields. Long and short of it, it may well be the case that the perceived variation in the expansion rate of the universe over time could be due to topology rather rather than some additional unseen dark matter or dark energy.
Sean Carroll had a great podcast with Adam Riess talking about this:
https://www.preposterousuniverse.com/podcast/2020/10/12/118-adam-riess-on-the-expansion-of-the-universe-and-a-crisis-in-cosmology/
How fast is the Universe Expanding? TOO FAST!
One thing bothers me about the CMB measurements as a whole, and it’s the Hubble ultra deep field photo (in case you haven’t seen it https://hubblesite.org/image/3886/category/58-hubble-ultra-deep-field )
Wherever we look in the Universe there are galaxies near the edge of the observable limit. Lots of them. The further we zoom in, the more we see….
So what happens to the ones that are on the edge, or just falling over it? Won’t the redshifts from these galaxies approach infinity – so some of the radiation would be redshifted from (say) 3000K, to (say) 2.7K at some point.
Furthermore, the deep field image shows entities that are far too small to be resolved by Planck. It will just be smudged in to the observations.
My point is that maybe this radiation is adding into the CMB, and if not taken into account, could increase the apparent CMB amplitude, and/or distort its spectrum slightly, or maybe even the polarisation, leading to the kind of offset of the Hubble constant derived from the Planck CMB observations.
I tried reading through the paper but the jargonese is too dense to digest easily without a lot of effort, maybe one day I’ll have time to read and understand it all….
In the mean time I was amused that there are “Planck Beams” and that they need calibrating (is the satellite made out of wood???? ;^)
So there are several answers here: the first is that yes, there are plenty of foreground objects that need to be subtracted from CMB measurements. However, this isn’t really that big a deal, because the important parameters for CMB measurements are *large-scale*: things that approach angular sizes on the order of degrees, and, well, far away galaxies are tiny and there are *lots* of degree-size patches on the sky.
The second point is that no, the redshift from a galaxy will never become big enough that starlight would be shifted down to CMB temperatures. Remember what the CMB *is* – it’s light from when the entire visible Universe was a ball of glowing hydrogen plasma. The entire Universe was 3000K at that point (the temperature that hydrogen turns into a plasma at those densities). It’s 2.7K now… because it’s at a redshift of ~1100. So you can’t have starlight (necessarily above a few thousand K) redshifted to 2.7K because… there weren’t stars then. In fact, there’s a big gap between the CMB (at a redshift of ~1100) and the point at which stars *could* form (at a redshift of ~20), because the Universe was just too hot for gravity to form stars. Note that the farthest galaxy we know of is at a redshift of ~11.
The other point to note is that your basic idea of “the further we zoom in, the more we see” is also not quite right. The CMB is *uniform* – it’s when the *entire Universe* was a ball of plasma. So obviously if you imagine the Universe expanding and forming galaxies clumping together, most of that structured Universe is going to be empty space. Which means if you pick a random direction and look deeper, and deeper, and deeper, most of the time you’ll just hit the CMB, and not a star or galaxy, with “dust and Milky Way gas” being the caveat there, since we’re embedded in them. Hence the reason why dust caused such a problem with CMB measurements a few years ago.
Pat, thanks for your considered reply, if I could clarify a few things.
Point 1, yes I was specifically talking about objects smaller than the angular resolution of Planck. The larger (angular size) objects are less problematic, I understand that.
Point 2. Are you saying that all stars that have ever existed are in the observable universe, and none have accelerated off beyond the horizon? Because if the latter, there must also be stars/galaxies that are indeed going over that horizon as we speak (from our point of view) and therefore these high redshifts are indeed attainable.
Point 3. We thought that, until that image from the HDF showed 3000 galaxies in a small patch of sky that was previously thought empty. Then a further zoom in (XDF) in the same area showed 5,500 galaxies in a smaller patch of sky. A separate deep field view towards the south showed similar results.
Have there been any HDF observations that show empty space? I.e. negative results? Please post some links to them, or cite them, it would be most interesting.
“Point 2. Are you saying that all stars that have ever existed are in the observable universe,”
No. I’m saying that *all stars that have ever existed, and whose light has reached us, are less redshifted than the light from the CMB that has reached us.* Remember redshift is *time*. Imagine this: pick a direction, look at the CMB there. That photon’s been travelling for roughly ~14 billion years to reach us. There are *no stars* whose light has travelled *more* than 14 billion years to reach us, because there were no stars more than 14 billion years ago. There certainly are stars *farther away* than that patch of sky that emitted that CMB, but their light hasn’t reached us yet.
Now imagine us at 1 Gyr later. That same patch of the Universe has cooled, and is emitting light as stars form. But the CMB is still behind it, because the CMB happened *everywhere*. Similarly, imagine those stars that were farther away before, as their light reaches us – the CMB is still behind *them*, too. The CMB is the *absolute furthest light we can see*. There will never be a galaxy more redshifted than it (or, in fact, even remotely *close* to it, due to the long time it took to form galaxies) because that light was emitted *far* before any galaxy could form, and it was emitted *everywhere*.
An interesting question you might ask is “wait… does this mean the CMB isn’t static over time?” and the answer to that is “yup, that’s exactly what it means.” The CMB we see *now* is not the CMB we will see in 1 Gyr, nor is it the CMB we would’ve seen 1 Gyr ago – *even if* you account for redshift and expansion. It should be *statistically* the same, however – although it’s not like we have billion-year experiments to test that!
—
Also, to be clear, the XDF is not a “zoom-in” of the HDF. It’s just a longer exposure – it’s a cop procedural’s “enhance.” They’re both very similar angular sizes – the XDF is a bit smaller, but not anything significant (maybe a third smaller in area – the HDF is ~2.6′-ish square, the HUDF is 2.4′-ish square, the XDF is 2.3’x2′-ish). And there’s a reason for that, too: astronomers *wouldn’t want* to actually zoom in, because far away galaxies *don’t grow smaller* – they actually grow *bigger*, albeit slowly. Basically, if I imagine a 1′ arc on the sky, that corresponds to around ~5 kpc at *every redshift past about 5*. Ethan Siegel has an article on this on Forbes’s Starts With A Bang which is very approachable.
So if I’m an astronomer, I don’t want a deep-field image at 1/10th the scale of HDF or XDF. That’d be terrible. Only a handful of galaxies would fit in it. But does that mean as you keep taking longer and longer exposures, the sky will completely fill in? If I take an *image*, sure, but that’s due to the finite resolution. If you *actually* zoom in, with finer resolution, you’d continually find more space between things (again, modulo gas and dust).
But uh, astronomers wouldn’t do that, because… if I want to see nothing, I can do that pretty easy. And getting *actually* zoomed in images requires bigger and bigger telescopes, whereas increasing the sensitivity just requires patience.
So just to really drill down into your point about stars being observable, and their relationship to the horizon…
If we think about 5Gy before now, and let’s imagine we had a Hubble HDF image from that time (and that humans existed to look at it….)
Are there any stars/galaxies on that image that have since accelerated to outside our current observable universe?
Or are you saying that all observable matter must always remain inside the observable universe, it can’t fall off the edge, as it were, no matter what the acceleration?
And furthermore, you’re saying that all stars and galaxies have an upper bound to their redshift, as observed from here. And that this upper bound must be << 1000. No matter where they formed, and no matter how much inflation has dilated the light since then?
I note with interest that you haven't cited any actual negative observation results (using similar equipment and exposure times to HDF).
“And furthermore, you’re saying that all stars and galaxies have an upper bound to their redshift, as observed from here. And that this upper bound must be << 1000. No matter where they formed, and no matter how much inflation has dilated the light since then?"
Inflation is a totally separate thing. Inflation essentially *defines* the Universe – moreso than the *observable* universe, and it occurred *before* the CMB. So you want to say "expansion" there. And the answer is "yes, yes, and yes." Because cosmic expansion has not dilated *any* light more than the CMB, because the CMB is older than any other light!
To be clear: the upper bound on redshift isn't fixed. It changes with time, as the Universe expands. *Redshift is time*. No stars can ever have a (cosmological!) redshift greater than the CMB because *no stars were formed before the CMB*. Saying "how can it be that there can't be a galaxy with redshift greater than the CMB" is equivalent to saying "how can it be that there were no galaxies *before* the CMB" and the answer to that's clear. All galaxies were formed *after* the time of the CMB, and the CMB is universal.
All galaxies' redshifts will increase over time as the Universe expands.
"Are there any stars/galaxies on that image that have since accelerated to outside our current observable universe?"
There's no easy way to answer that question because you haven't defined what "accelerated outside our current observable universe" means. For instance, I could ask "do you mean, are there any galaxies that were there that we cannot see anymore?" to which the answer is "absolutely not." No galaxies have "winked out."
But let me try to answer by just imagining, say, that same GN-z11 galaxy, which is currently at redshift 11. What will happen to it, with time?
Over time, that galaxy's redshift will grow. Redshift=time. So z will go from 11, to 12, etc. The image will grow progressively redder – wavelengths will stretch with time. But the image from it *never* (theoretically) goes away. Ever. They do become unobservable, though! Imagine the CMB redshifting to become the cosmic radio background, then the cosmic "ultra-low frequency" background. At some point the image is *so* redshifted it's impossible to view, but from a "continuum" point of view it's still there. If you define the "last possible photon" as a photon which fits inside the observable Universe, then at some point, the image winks out completely.
Note – before this *ever* happens to any galaxy *ever* observed, it will happen to the CMB first. Because the CMB's older! So has this happened to any galaxy – ever? No. The Universe isn't old enough!
But *think about what it means* when the image becomes redshifted. Imagine if that light was from a cesium clock: originally it was 9.2 Gcycles every second. Now imagine it's down to 1 cycle/second. That means it would take you 9.2 billion seconds to observe *one second* from those galaxies! And because the redshift is *accelerating*, that means the time needed to observe *two seconds* is even longer. So in fact, you could do the integral: ask "if I watch this galaxy *until infinity*, how much time will I see from this galaxy?" and the answer is *finite*.
So, that means there are *times* that that galaxies exists at that you can *never observe*. The galaxy never "disappears" from your view (in the continuous limit). The images from that galaxy just slow, and slow, and slow. Again, in the "last possible photon" limit (where you define a *lower limit* to a photon's energy), it will wink out. But the universe is *nowhere near* old enough for that.
If this sounds like what happens when a person falls into a black hole as observed from outside… it's because it is.
—
I answered the HDF question previously.
Been following your comments with interest – and I want to “zoom in” (if you’ll pardon the pun) on this element:
“But does that mean as you keep taking longer and longer exposures, the sky will completely fill in? If I take an *image*, sure, but that’s due to the finite resolution. If you *actually* zoom in, with finer resolution, you’d continually find more space between things (again, modulo gas and dust).”
I’m curious on this: how would we be able to tell the difference between the two? If our understanding is based on images, and the images are limited by finite resolution, do we know if we would find “empty patches” at high enough resolution? Or is it possible that, “zooming in” like you get to do in some computer space simulations doesn’t actually reveal a perspective very similar to ours, of a different observable universe?
Put another way: if I could “look” far enough at any patch of sky, would I ever see a spot that was dark, forever? Or is there always a star/object out there if I “look” far enough? And with either answer, how do we know it?
On a separate point, one question I’ve often wondered about CMB, that I think is supported by your comments in the chat here, is if CMB is more of a limit or an average. If so, it seems like there could plausibly be a lot more explanations for it than the standard cosmological model provides.
I guess the big question: do astronomers posit that our standard cosmological model is necessarily true? Or, are there alternative models that use different variables you’ve described (varying cosmological constants vs motion, etc.) to make sense of the observed data? If there are other theories, any suggested sources for reputable ones vs ones that are do not make sense of the empirical data?
Or, in other words, how likely are we to see the “new physics” the original article teases as a possibility?
> He showed that the Cepheid stars were not located within our galaxy and that nebulae are actually distant galaxies.
Correction, nebulae are not distant galaxies. I think you perhaps meant that the nebulae are IN different galaxies.
Originally, the word “nebula” was used for any cloudy patch and it was thought that all such were within our galaxy. Then Hubble proved that the Andromeda “Nebula” was actually the Andromeda Galaxy and now the word “nebula” is used to specifically refer to a cloud of dust or gas and not just “any diffuse object in the skies.”
Now that you mentioned the historical context, I also remembered this bit of historical trivia. I definitely recommend that sentence be add this context, otherwise the description is quite confusing.
Back then galaxies were thought to be nebulae in our galaxy. He showed they were outside. Nebulae in other galaxies are generally too small to see.
Cosmology isn’t science
None of this can be tested