An unfortunate reality of trying to represent continuous real numbers in a fixed space (e.g. with a limited number of bits) is that this comes with an inevitable loss of both precision and accuracy. Although floating point arithmetic standards – like the commonly used IEEE 754 – seek to minimize this error, it’s inevitable that across the range of a floating point variable loss of precision occurs. This is what [exozy] demonstrates, by showing just how big the error can get when performing a simple division of the exponential of an input value by the original value. This results in an amazing error of over 10%, which leads to the question of how to best fix this.
Obviously, if you have the option, you can simply increase the precision of the floating point variable, from 32-bit to 64- or even 256-bit, but this only gets you so far. The solution which [exozy] shows here involves using redundant computation by inverting the result of ex. In a demonstration using Python code (which uses IEEE 754 double precision internally), this almost eradicates the error. Other than proving that floating point arithmetic is cursed, this also raises the question of why this works.
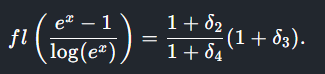
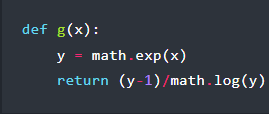
For the explanation some basic understanding of calculus is rather helpful, as [exozy] looks at the original function (f(x)) and the version with the logarithm added (g(x)). With an assumption made about the error resulting with each arithmetic operation (δ), the two functions can be analyzed, adding a 1 + δ assumption following each of these operations and simplifying them as much as possible. For f(x) it becomes clear that it is the denominator which is the cause of the error, but we have to look at g(x) to make sense of what changes.
Intuitively, log(ex) helps because it somehow cancels out the error in ex, but what really happens is that with the small inputs used for x (g(1e-9), g(1e-12) and g(1e-15)) the approximations result in the simplified breakdown shown here (fl()). With a larger x, the Taylor series expansions used in the analysis no longer apply. What seemed like a fix no longer works, and we are left with the stark realization that representing real numbers in a fixed space will forever be the domain of tears and shattered dreams.
















shattered dreams are also in representing fixed precision decimal in binary. at least in finance.
It is still better than 32bit float – but yes, if it is money, you should know what you are doing (or cry)
Maybe this is where Fijitsu went wrong in the Great British Post Office Scandal?
Use rational arithmetic for money. The results are exact.
I’m 99.00001% sure that most programmers don’t understand just how cursed using floating point numbers is, when dynamic range isn’t needed. Fixed point is so easy to implement that it doesn’t need libraries and dedicated hardware, but having libraries and dedicated hardware seems to push everyone to default to more difficult and resource intensive floating point, even for applications where it’s far worse than fixed point.
Fixed point is a different space of problems. Fixed point is good when all the numbers are similar in scale and you care about absolute error. Floating point is good for a large dynamic scale and your more interested in relative error.
yeah like Marc said…they each have their places. and these days, i don’t see any particular merit to the claim “more resource intensive floating point” — just about everything bigger than an rp2040 has a powerful FPU these days. when i first learned about FP math, i thought “gee that’s complicated” but now i’ve been stuck in the guts of it for a decade and the basic mulitply and add operations are not really that complicated, not intrinsically slow. they do require a lot of transistors but it’s 2024 and moore’s law has gifted us with more transistors than we can shake a stick at.
i am saying this because in like 2003 i envisioned a piece of software where the motivation that made me write it is i realized i could do it all in fixed-point math. before i had that realization, the performance requirements simply didn’t seem plausible to me. so it was a big hack and i did it. but a few years later, on a lark, i reimplemented it in floating point. it was faster (because it elided extra operations that were necessary to make the fixed point hack) and the results were better. i hadn’t really thought about it properly, but actually the scales were different and it really did prefer to have floats. never looked back.
i always use fixed if i want fixed. and i always use float if i want float. sigh.
Still, it’s a relief going from the kind of organization that exclusively uses fixed point types to one the uses floats. A clear progression. Makes you go ‘Ahhhh! I had stopped noticing how bad that was, until it went away.’
Not that having engineers for customers is cake, but better then the alternative. Much much much better than MBAs or marketers.
If you use fixed points exclusively you are overhead. Marketing runs your business.
There might be exceptions, but they are rare.
Some undergrad computational physics taught me some lessons about floats, many of which I have forgot
1) 1/(x+delta – x) where delta is a very small number, e.g., a time step, is a very bad idea
2) play around with constants so that most math happens around 10^1 sized numbers, floats are ‘denser’ closer to zero, but you get funny behaviour too close to zero
3) (may no longer apply) avoid division where possible
A nice opportunity to mention the classic article “What every computer scientist should know about floating-point arithmetic” by David Goldberg,
https://dl.acm.org/doi/10.1145/103162.103163
and one of many, many articles inspired on it,
https://www.volkerschatz.com/science/float.html
Even more basically. If you don’t want to learn the basics of floating point then this one factoid is useful: You don’t want to subtract two values (including addition if either could have opposite signs) when then could be almost the same value (if it can be avoid). You’re cancelling out the high digits and pulling up small errors. This is termed “catastrophic cancellation”. In this specific example exp(x) is near 1 when ‘x’ in near zero. exp(x)-1 is a common quantity to want to compute so whatever math library is being used with almost certainly have a special case function for it. Typically it’s called ‘expm1’ so expm1(x)/x is going to be a better way to compute this value.
Despite its colorful name, catastrophic cancellation isn’t itself a problem. It can be a symptom of a problem, though.
The issue expm1 (and its inverse, log1p) is that e^x is near 1 when x is near zero. If you compute e^x – 1 as two steps—first the exponential, and then the subtraction—you will get catastrophic cancellation when x is near zero. That cancellation is a *symptom*, not a cause.
Consider that e^0.01 ≈ 1.01005, e^0.001 ≈ 1.0010005, e^0.0000001 ≈ 1.0000001. To a first order, e^x ≈ 1 + x when x is small. Computing (1 + x) – 1 does result in catastrophic cancellation. The actual numeric damage comes from 1 being much larger than x, and so we lose precision on the interesting part of the number.
And log1p (which computes log(1 + x)) allows you to round-trip with decent accuracy: expm1(log1p(x)) and log1p(expm1(x)) should give you a value very close to x when x is near 0.
The expm1 and logp1 build that offset of 1 into their calculations, so that the distance between the leading 1 of the values and the LSB of the actually significant bits doesn’t get so far apart.
But remember: catastrophic cancellation is the *symptom*, not the cause.
yeah i came here to write this too! when i first read the article, i thought “gee why is this so complicated with the log and exponential”…the write up left me scratching my head, unable to immediately understand it. but i saw it again today and realized what the article should have said, what you said.
the rule is, don’t use addition and subtraction with vastly different scales. float is going to roughly enforce these three invariants:
big + tiny = big + err0
big – tiny = big – err0
big1 – big2 = err0
where err0 is a severely-rounded result that will tend to become 0 (underflow).
learned this the fun way debugging a compiler using a test case copied from a popular textbook that had that mistake in spades. i don’t know if it made those algorithms unusable for people who read the book, but for my purpose it meant most of the tests simply only reported rounding noise and no signal. for a multi-platform compiler, multiple flavors of rounding noise is kinda-sorta inevitable and it really limited the utility of that test.
Once upon a time as an engineering undergrad (computer option) I took a course in math analysis. Which was simply about all the ways that computer math can fail you. Presumably something similar is still available.
How about an arduino example reading voltage on analogue pin?
Use an analog log converter between the sensor and the ADC pin if you expect more than (or even about) a decade of dynamic range from your sensor. Then do exp(x) in software.
If anyone is interested in a writeup of why, I’d be kind of into doing it.
A tool to help automatically rewrite floating point calculations for accuracy: https://herbie.uwplse.org/
That’s fantastic! I learned a lot of these tricks as an undergrad doing computational physics programming, through Numerical Recipes but also through word of mouth — in classes. It’s awesome to see them turned into something like a math compiler.
I bet it’s still useful to learn about the pathological ways to phrase equations for computers, because it teaches you something about the machine that you’re using. But if the “compiler” works well enough, there’s no reason to write assembly by hand either.
On most systems – something as simple as below will give you different answers.
#include
#define MAX 10000000
int main(int a, char **b) {
float sum = 0, mus = 0;
for(int i = 0; i = 0; i -= 100)
mus += i;
printf(“forward %f\n”, sum);
printf(“backward %f\n”, mus);
return 0;
};
On *all* systems that won’t compile, and even if it did sum and mus are both going to wind up 0.0.
Semicolon!
We found the ChatGPT ‘programmer’. Burn him!
Nah. You are shooting from the hip. I suspect the missing code there is angle bracket open stdlib.h angle bracket close.
And with that it does compile, run and yield the expected to slightly different sums for me on osx.
Peter
No it doesn’t.
non-fatal: MAX is defined but never used and there is a dangling semi-colon.
Fatal:
The ‘for’ loop uses an assignment instead of a comparison. If your compiler accepts that and you run it the test is always false so it will run forever or until it crashes, whichever comes first.
If your compiler is modern it will not compile by default with that mistake, so you fix the assigned to a comparison and now it initializes to 0 and tests for 0 so never runs even once thru the loop.
Since the loop is skipped the output will be the initialized values, always 0.00000:
% ./a.out
forward 0.000000
backward 0.000000
% uname -a
… Darwin Kernel Version 23.4.0: Fri Mar 15 00:12:41 PDT 2024; root:xnu-10063.101.17~1/RELEASE_ARM64_T8103 arm64
Hi,
i miss the calculation for sum.
So, trying to reinvent formulas that game devs and others have known since the 80s?
I believe the need for expm1() and log1p() due to e^x ≈ 1 + x for small x was known well before the 1980s. It was probably known before I was born in the mid 1970s.
I at least found one Fortran IV manual that mentions the numerical issue, but not the remedy. I haven’t found where these first started filtering into math libraries.
The leading term of e^x’s Taylor series is 1, and it sticks out like a sore thumb if you know x is going to be small.
Can I mention climate simulations, or will that trigger somebody? 😼