Most people know about the numerical constant pi (or π, if you prefer). But did you know that pi has an evil twin represented by the symbol ϖ? As [John Carlos Baez] explains, it and its related functions are related to the lemniscate as pi relates to circles. What’s a lemniscate? That’s the proper name for the infinity sign (∞).
[John] shows how many of the same formulas for pi also work for the lemniscate constant (the name for ϖ). Some (as John calls them) “mutant” trig functions use the pi-like constant.
Mathematically, a circle is a point (the center) with a curve that describes x2+y2=r2. The lemniscate is a particular instance of a Cassini oval where r2=cos2θ. We all know the circumference of a circle—basically, the perimeter—is 2π; the perimeter of the lemniscate is 2ϖ.
Why does any of this matter? Well, [John] shows how it connects to elliptic curves and the Gauss constant.
Like pi, the lemniscate constant probably never ends, but it is roughly 2.622057. Will this be useful in your next project? Probably not. Will it help you win some bar bets? Maybe.
Then again, if you are bored calculating more digits of pi, here’s something new to try. Not that you need that many digits.

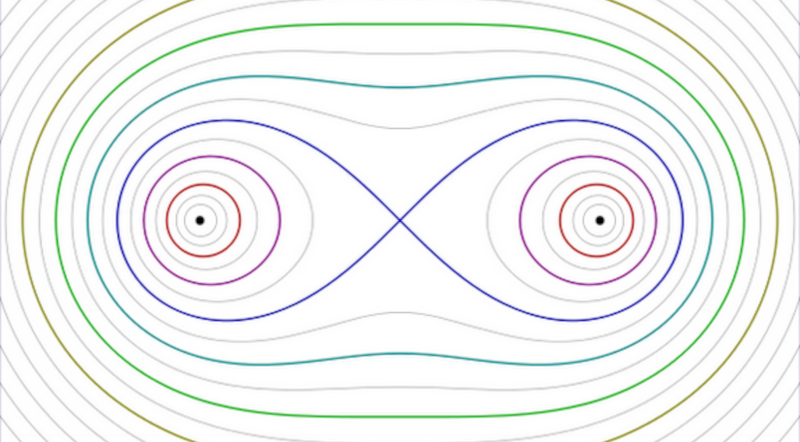















So, if lemmings could wear skates, would they move around in Figure-8s?
Merry Christmas all you mad HADders!
Merry Christmas, Ren!
The circumfrance of a circle is 2πr not 2π.
I never understood why it’s not π2r or 2rπ to reflect relation between diameter and π rather than double π (τ) and radius.
I just notice, τ is twice as big as π but if you cut π symbol vertically you will get something like double τ. Look: ττ vs π. Symbols are all wrong! ;-)
Merry Christmas.
@PPJ maybe because the generic formula is arc_length = angle * radius, so circumference = 2*pi radians * radius
It is for a circle of r=1, which I think is implied by x² + y² = r² earlier in the sentence, but that too had a formatting error, they’re probably just drunk because it’s Xmas :-D
“It is for a circle of r=1, which I think is implied by x² + y² = r²”
Not imπlied at all. Let r=5 or 10 or 8. The unit circle is for convenience, not a law of nature.
“Like pi, the lemniscate constant probably never ends”
Now this confuses me. Does it mean π probably never ends? ‘The lemniscate constant is like π which probably never ends’?
Or ‘The lemniscate constant is probably like π which never ends’?
Or ‘Can’t be arsed to look it up, that should hold the little bastards!’?
Or ‘ϖ is transcendental, irrational, and here’s the kicker Danno, never ends.’?
I accept that’s it’s a (probably written/cursive) variant of π but in type it begs to be called “omega bar”.
“It is for a circle of r=1, which I think is implied by x² + y² = r²”
Not imπlied at all. Let r=5 or 10 or 8. The unit circle is for convenience, not a law of nature.
“Like pi, the lemniscate constant probably never ends”
Now this confuses me. Does it mean π probably never ends? ‘The lemniscate constant is like π which probably never ends’?
Or ‘The lemniscate constant is probably like π which never ends’?
Or ‘Can’t be arsed to look it up, that should hold the little bastards!’?
Or ‘ϖ is transcendental, irrational, and here’s the kicker Danno, never ends.’?
I accept that’s it’s a (probably written/cursive) variant of π but in type it begs to be called “omega bar”.
@PPJ: as a general rule constants expressed as numbers are placed before constants expressed as symbols, and constants are placed before variables.
It’s a transcendental number, so it definitely never ends.
You don’t even have to go there: irrational is enough. A number with finite digits in any integer base is rational.
looks like boobs to me 🤷♂️
yeah ,definitely boobs. anyone else see boobs? we can start a trend! or a cult to ϖ who knows :)
B | oo | b
top view | front view | side view
Merry Christmas, Hackaday. My god
Hmm, so that’s what boobs look like.
Heino’s eyes is what it evokes for me.
Heretic!
Yes it does actually resemble Circumareolar Langer’s lines.
Never heard of that before… interesting. Learn something new every day!
“Mathematically, a circle is a point (the center) with a curve that describes x2+y2=r2.”
Which can be simplified to x+y=r. Or did you mean to write x²+y²=r²?
WordPress is killing me…
“Like pi, the lemniscate constant probably never ends, but it is roughly 2.622057.”
… Uh, both numbers have been proven to be transcendental. It is absolutely certain that neither one ends or repeats.
Actually it doesn’t repeat for either as far as we have calculated. Might, but we’re not there yet.
if it was periodic, it would also be rational, so it can’t be
Yup: because the repeating pattern can just be recast as a geometric series, which is just a fraction.
The whole “never repeats or ends” is just a statement about irrationality. Any repeating number in base 10 can be a no repeating number in a different integer base.
So could this evil twin be called Anti-Pi ? So then in that alternate universe is pi R round ? Is that the alternate universe where Spock had a beard ?
Merry Christmas and A Hacking New Year.
Why not just put a goatee on Pi?
Oops just saw someone beat me to it
I mean it kind of looks like it, except it got no legs, and no cool hat :-(
Merry Christmas (or whatever you celebrate)
It’s an important figure in optical mineralogy. They appear in spectacular color between crossed polars if the viewing axis is correct in an biaxial crystal.
For all of us who don’t immediately recognize obscure Greek letters, that symbol is also pi. Wikipedia says it’s a “glyph variant of lower-case pi”: https://en.wiktionary.org/wiki/%CF%96
I guess it’s just pronounced “pi”, just the same? We don’t voice a difference in capital or lower case letters anywhere else. I have no idea, honestly, so if you do, please enlighten us!
On account of the holiday I’ll withhold my thoughts on mathematics’ noob-friendliness…
Replying to myself here, it’s apparently pronounced “varpi”, as in “variant of pi”, which is so perfectly obvious I can’t imagine why more people don’t jump right into mathematics. There’s no barrier to entry at all!
/s
The circumference of a circle is 2pir, not 2*pi. It’s only 2pi if the radius happens to be 1
The decimal representation of the lemniscate constant doesn’t “probably never end.” It is provable that it never ends. It is a fact, it is not in doubt. This is because it is a transcendental number and all transcendental numbers are irrational
Just irrationality is needed: the proof pi is transcendental is harder than the irrationality proof (at least in my opinion). You can prove pi is irrational a bunch of ways.