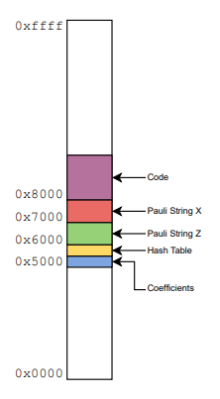
the implementation, as set within the address space of the Commodore 64 – about 15kB of the accessible 64kB RAM is used.
There’s been a lot of fuss about the ‘quantum advantage’ that would arise from the use of quantum processors and quantum systems in general. Yet in this high-noise, high-uncertainty era of quantum computing it seems fair to say that the advantage part is a bit of a stretch. Most recently an anonymous paper (PDF, starts at page 199) takes IBM’s claims with its 127-bit Eagle quantum processor to its ludicrous conclusion by running the same Trotterized Ising model on the ~1 MHz MOS 6510 processor in a Commodore 64. (Worth noting: this paper was submitted to Sigbovik, the conference of the Association for Computational Heresy.)
We previously covered the same claims by IBM already getting walloped by another group of researchers (Tindall et al., 2024) using a tensor network on a classical computer. The anonymous submitter of the Sigbovik paper based their experiment on a January 2024 research paper by [Tomislav Begušić] and colleagues as published in Science Advances. These researchers also used a classical tensor network to run the IBM experiment many times faster and more accurately, which the anonymous researcher(s) took as the basis for a version that runs on the C64 in a mere 15 kB of RAM, with the code put on an Atmel AT28C256 ROM inside a cartridge which the C64 then ran from.
The same sparse Pauli dynamics algorithm was used as by [Tomislav Begušić] et al., with some limitations due to the limited amount of RAM, implementing it in 6502 assembly. Although the C64 is ~300,000x slower per datapoint than a modern laptop, it does this much more efficiently than the quantum processor, and without the high error rate. Yes, that means that a compute cluster of Commodore 64s can likely outperform a ‘please call us for a quote’ quantum system depending on which linear algebra problem you’re trying to solve. Quantum computers may yet have their application, but this isn’t it, yet.
Thanks to [Stephen Walters] and [Pio] for the tip.