Reverse-Engineering The Polynomial Constants In The Pentium’s FPU

January 5, 2025 by Maya Posch 5 Comments

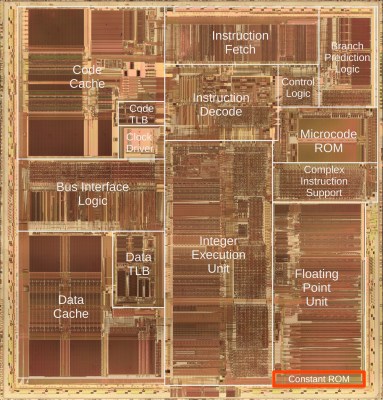
Die photo of the Intel Pentium processor with the floating point constant ROM highlighted in red. (Credit: Ken Shirriff)

Released in 1993, Intel’s Pentium processor was a marvel of technological progress. Its floating point unit (FPU) was a big improvement over its predecessors that still used the venerable CORDIC algorithm. In a recent blog post [Ken Shirriff] takes an up-close look at the FPU and associated ROMs in the Pentium die that enable its use of polynomials. Even with 3.1 million transistors, the Pentium die is still on a large enough process node that it can be readily analyzed with an optical microscope.

In the blog post, [Ken] shows how you can see the constants in each ROM section, with each bit set as either a transistor (‘1’) or no transistor (‘0’), making read-out very easy. The example looks at the constant of pi, which the Pentium’s FPU has stored as a version with no fewer than 67 significand bits along with its exponent.

Continue reading “Reverse-Engineering The Polynomial Constants In The Pentium’s FPU” →

The Quadratic Equation Solution A Few Thousand Years In The Making

January 3, 2020 by Al Williams 38 Comments

Everyone learns (and some readers maybe still remember) the quadratic formula. It’s a pillar of algebra and allows you to solve equations like Ax²+Bx+C=0. But just because you’ve used it doesn’t mean you know how to come up with the formula itself. It’s a bear to derive so the vast majority of us simply memorize the formula. A Carnegie Mellon mathematician named Po-Shen Loh didn’t expect to find a new way to derive the solution when he was reviewing math materials for middle school use to make them easier to understand. After all, people have been solving that equation for about 4,000 years. But that’s exactly what he did.

Before we look at the new solution, let’s talk about why you want to solve quadratic equations. They are used in many contexts. In ancient times you might use them to determine how much more crop to grow to cover pay tax payments without eating in to the crop you needed to subsist. In physics, it can describe motion. There’s seemingly no end to how many things you can describe with a quadratic equation.

Babylonians, in particular, would solve simultaneous equations to find the roots of a quadratic. Egyptians, Grecians, Indians, and Chinese peoples used graphical methods to solve the equations. The entire history is a bit much to get into, but still a great read. For this article, let’s dig into how the new derivation was discovered.

Continue reading “The Quadratic Equation Solution A Few Thousand Years In The Making” →