3D-scanning seems like a straightforward process — put the subject inside a motion control gantry, bounce light off the surface, measure the reflections, and do some math to reconstruct the shape in three dimensions. But traditional 3D-scanning isn’t good for subjects with complex topologies and lots of nooks and crannies that light can’t get to. Which is why volumetric 3D-scanning could become an important tool someday.
As the name implies, volumetric scanning relies on measuring the change in volume of a medium as an object is moved through it. In the case of [Kfir Aberman] and [Oren Katzir]’s “dip scanning” method, the medium is a tank of water whose level is measured to a high precision with a float sensor. The object to be scanned is dipped slowly into the water by a robot as data is gathered. The robot removes the object, changes the orientation, and dips again. Dipping is repeated until enough data has been collected to run through a transformation algorithm that can reconstruct the shape of the object. Anywhere the water can reach can be scanned, and the video below shows how good the results can be with enough data. Full details are available in the PDF of their paper.
While optical 3D-scanning with the standard turntable and laser configuration will probably be around for a while, dip scanning seems like a powerful method for getting topological data using really simple equipment.
[wpvideo xx88I1SN]
Thanks to [bmsleight] for the tip.

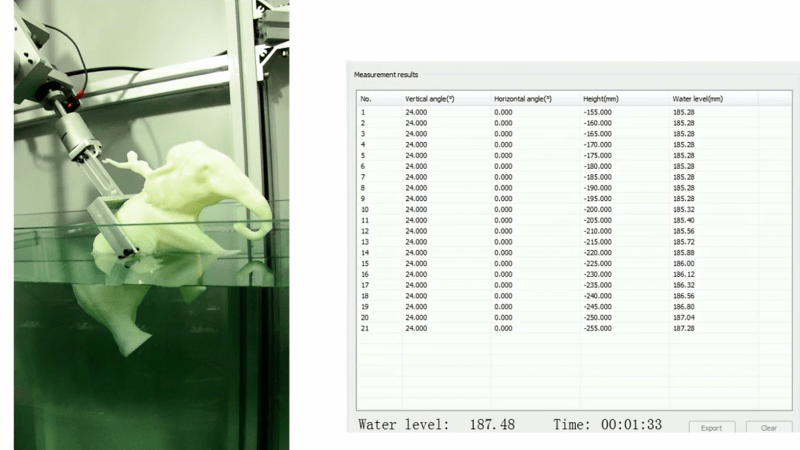














Wow!
Could one speed things up rotating the object and by that only dipping it once?
May be… for instance using a horizontal arm. First dip the object vertically till the central axis of the arm is at water level and then start rotating on the horizontal axis….
That would just be dipping partially on a different axis
Alan Resnick did it first https://www.youtube.com/watch?v=66X9wwEyMLk :D
It’s similar in appearance but based on a very different approach. Not the same.
Well that approach is basically simulating a depth map by occluding the object based on the depth of the water. So it is still vision based.
The approach above doesn’t need a camera just equipment sensitive enough to measure the volume in a cube.
Makes me wonder how it would deal with a model that would trap air inside itself at certain angles…
Thinking about how they calculate all the possible permutations of how much water is displaced and the shape of the displacing object is hurting my brain.
That must be phenomenally complex.
It sounds similar to how CT data is reconstructed, which is surprisingly simple.
I’m a bit surprised they’re using water for this. Isopropanol is cheap, readily available, and only has about a third the surface tension of water. I would expect it to increase measurement accuracy, especially in small volumes of liquid in larger-diameter tanks where the meniscus might represent a significant source of error.
I also wonder about cavities that form air pockets during submersion in some orientations. Do they have a way to compensate for them?
Isopropanol is also a solvent though and there are ways to lower water’s surface tension without making it flammable and more evaporative. At least the surface tension effect is consistent though if the medium stays the same but differing geometry is going to impact that as the object is lowered in.
Air pockets that suddenly fill up as the object is dipped could be a significant problem.
Doing this to absorbent objects like a tissue paper elephant could be an big issue and many materials that you typically think of as not absorbing any water will actually absorb a half a percent or a percent or so if left submerged long enough.
isopropanol evaporates rather quickly.
also:
https://en.wikipedia.org/wiki/Isopropyl_alcohol#Safety
https://en.wikipedia.org/wiki/Isopropyl_alcohol#Toxicology
Here is one water surface tension reduction method.
http://www.esrf.eu/UsersAndScience/Publications/Highlights/2005/SCM/SCM1
“A bi-molecular layer of a three-tailed amphiphile drastically enhances capillary wave fluctuations on water surface due to a reduction in surface tension to 1 mN/m.”
Water is normally 72 mN/m. Alcohol is around 20 mN/m.
Um, couldn’t you just… add soap?
That works down to take it down to mid 20’s or so. But then you also get bubbles.
Maybe add some kind of defoamer? Simethicone maybe? It’s easely avaible in pharmacies.
in (wet) photodeveopment a ‘wetting agant’ is used which is a non foaming meniscus reducer. I’d use that. still not sure how to get round air pockets though
Regardung the bubbles you’d just need a different surfactant, for example polydimethylsiloxane which is a surfactant and an antifoam agent.
Interesting, this seems to be the more common name for Dimethicone (which i called _S_imethicone but that is wrong, it’s Dimethicone with added silicon dioxide or something like this. Chemistry is strange stuff…).
I fail to see how this alone is able to reconstruct the topological data? It seems to potentially augment or refine existing data sets though but the video appears to show it capturing surface geometry level detail?
It’s like those grid puzzles where you deduce which cells are filled from the count of filled cells per row/column. Also like computed tomography.
Distilling the 2d section into a single displacement quantity is why it requires thousands of immersions to achieve detail where a laser line scanner would only take hundreds.
How does one reconstruct the surface detail to any degree of accuracy though with no optical or other scanning capability?
The same way you convert any other group of lower-dimensionality records of a thing into a higher-dimension representation.
CT scans are already 1d projections of a 3d thing. (Look up a sinogram)
CT scans lose the topography detail as well though. Things like skin texture or other “high resolution” specific features.
This is some serious clever DSP application there. I never heard of something so smart since data post-processing for NMR scanning. Very impressing!
Sounds like GlaDOS from Portal has now a new job…
Pretty cool.
Probably not the best method for scanning people or pets though…
just thought someone might benefit from that warning
It’s ok. We’ll dry the kitten in the microwave afterwards… :)
I really love this way of thinking outside the box. I’m sure that this dipping method will be a positive contribution to solving the problems of 3D scanning. Thanks for posting.
Accuracy could possibly be improved by shaking off excess liquid between scans, and maybe vertical baffles for the tank walls to suppress waves.
I don’t think either of those things is actually much of a problem, given that they’re doing 1000+ scans. You essentially get massive oversampling that will smooth out any per-scan noise.
But, if noise is reduced then fewer scans would be required for comparable quality.
But the high number of scans is due to how tomography works – to get high resolution you need a large number of scans even if there was no noise.
Hackaday, please add a “like” button.
Not for comments, but for articles like this.
+1
Just send a note to the author’s boss asking for a raise. Much better than kudos.
http://irc.cs.sdu.edu.cn/3dshape/files/paper.pdf
That’s the original paper.
WordPress spambots seem to be able to like my comments just fine…
Like, share, and subscribe? Send the links to your friends?
But yeah, noted. And “liked”.
That is a very innovative application of Tomosynthesis, however the scan times would be very long as “sloshing” would limit the dip rate. There would be limits on the types of objects that can be scanned too, or you need to come up with a removable hydrophobic coating that you can dip seal the object with first. If you can use a tank liquid with a low freezing point and low viscosity that is chemically inert you may be able to find a compound that can be used as a sealant at those temperatures but melts then evaporates away at higher temperatures leaving the object as it was before the scanning operation.
yes, I was wondering about the sloshing about and if they need to wait a long time for it to settle. Maybe you could use something like opencv to get a picture of the ‘waves’, and then just calculate what the ‘flat’ surface would look like (would probably need to do this across the whole 2d surface though, which might be tricky). You could probably calibrate this first with a few runs, to get a decent algorithm.
I guess with enough computational power, slosh is a wave after all so the zero could be located if you know the extrema.
I’m not sure this makes sense, since you only measure volume you would only get one dimension per dip.
Doesn’t make sense to me that this works with all objects in any appreciable time, I would think symmetrical protrusions would make it rather hard to determine the shape that way requiring ever more dips or high precision leading to the need of a immense amount of dips and an crazy precision in measurement too. Making me think they represent it as a bit too easy.
Also the video claims they normally only use light/vision but they have been using prodding probes for decades too. So that claim is incorrect.
It’s the multiple dips at different angles that give you the data you need for a reconstruction. It’s very similar to how CT data is reconstructed. Look up sinograms to give you a better idea of the math behind this.
Well I get the concept, but it remains a very very slow process needing very very small increment and many many angles for certain type of objects surely.. And even then I imagine there can be objects that defy the algorithm/medium.
It’s like you were scanning with a needlepoint laser except much slower because you would need to wait 5+ seconds for the object to be stable with each tiny point.
Thanks for replying though. Although I have to say, with CT scans you do get a cross section 2-dimensional set of data points AFAIK and not a set of single 1 dimensional data-points as this method seems to render.
Archimedes today would add a load cell on a dip arm, and thus made this apparatus scan not only the shape, but also a density distribution inside it, which would give answer to here not asked question: “Is there an weight hidden somewhere inside this elephant?”, or “is this part of homogeneous composition?”, or “is this dice rigged?”
The buoyancy is a function of volume, not of how mass is distributed within the volume. A vertical only load cell would give data redundant with the fluid level change. But measuring torque from buoyancy would give some information regarding the distribution of volume along horizontal axis.
I’m having a difficult time wrapping my head around this mathematics of this method…
Could someone let me know if it would accurately reproduce these objects, or would it just appear to be a sphere?
https://youtube.com/watch?v=2eUWT9cI23o
I belive the method would still work. As far as I understand these shapes have a constant MAXIMUM width on any arbitrary axis, as such they would be possible to distinquish from a sphere. At any other point, than at the MAXIMUM width, the slice area may differ from that of a sphere.
It was bugging me, and I’ve no way to test it out. I think there is some geometry that would mess things up.
The maximum width thing went right over my head.
Thanks for responding!