The philosopher in the street, who has not suffered a course in quantum mechanics, is quite unimpressed by the [Einstein-Podolsky-Rosen] correlations. He can point to many examples of similar correlations in everyday life. The case of Bertlmann’s socks is often cited. Dr. Bertlmann likes to wear two socks of different colours. Which colour he will have on a given foot on a given day is quite unpredictable. But when you see that the first sock is pink you can be already sure that the second sock will not be pink. Observation of the first, and experience with Bertlmann, gives the immediate information about the second. There is no accounting for tastes, but apart from that there is no mystery here. And is this [Einstein-Podolsky-Rosen] business just the same?
John Bell began his now famous paper with the above paragraph. The Bell Inequality started off like so many other great theories in science – as a simple thought experiment. Its conclusions were not so simple, however, and would lead the way to the end of Einstein’s idea of local hidden variables, and along with it his hopes for a deterministic universe. In this article, we’re going to look at the Bell inequality in great detail. Our guide will be a chapter from Jim Baggots’ The Quantum Story, as it has one of the best descriptions of Bell’s theory I’ve ever read.
Before we start – a quick review:
Niels Bohr’s Quantum Theory says reality is probabilistic in nature. Einstein disagreed, and spent the latter part of his life trying to prove Bohr wrong. It culminated into a thought experiment known as the EPR paradox. This is where Einstein introduced his local hidden variables theory. But John Bell was able to prove that it was possible to show that local hidden variables could not account for all the predictions of quantum theory. Einstein was never able to recover from this defeat and technology would eventually advance enough to test Bell’s theory, proving Einstein wrong. This is the story about how John Bell achieved this remarkable feat.
How To Make A Local Hidden Variable Theory
Let us consider a fragmented pair of hydrogen atoms whose total spin is equal to zero. We send both atoms speeding away in opposite directions. We then measure the spin of one of the atoms using a [Stern-Gerlach] device – which is just two magnets with opposite poles resting very close to each other.
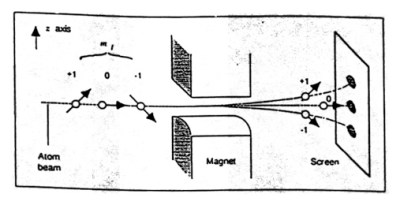
When a spinning particle, or in our case a hydrogen atom, passes between the poles, the direction of the spin can be determined by the direction the atom is deflected. We say an atom with a “spin up” is one that is deflected to the north magnetic pole and designated “+”. Likewise, an atom with an opposite spin will be in a “spin down” state, and will be deflected to the south magnetic pole. Its designation is “-“.
Back to the case of our pair of fragmented hydrogen atoms – when we measure the spin of one we can determine what the spin of the other is, as they have to be opposite. Einstein would say that the spin of each of the atoms was determined at the moment of fragmentation… that there is some type of hidden variable within each of the atoms that determines the spin. Remember that quantum theory says the spin of the two fragmented atoms cannot be known until one is measured. And somehow when one spin is measured, the other atom must know to take the opposite spin. This is the heart of the EPR paradox.

Now, lets look at this local hidden variable idea the way John Bell did. Let us suppose that each atom has a little hidden dial deep within one of its many subatomic particles. A dial that has yet to be discovered. The dial can point in any direction from 0 to 360 degrees. Each of our hydrogen atoms has one of these dials, and when they are paired, the dials point in opposite directions. When the atoms become unpaired, the dials become fixed, as pictured in the figure on the left.
Now let’s pass our atoms through the [Stern-Gerlach] spin detector. With our newfound knowledge of the hidden dial, we find that the atoms get deflected to whatever direction the dial is pointing. Such that if the dial in the atom is anywhere in the top half of the dial face, the atom will have a spin up, or “+” property, and if the dial in the atom is pointing in the bottom half, it will have a spin down, or “-” property. We have created a very basic hidden variable theory. We will soon find out, however, that it’s all we really need to show its limitations compared to quantum theory.
Thinking Outside the Quantum Box
With knowledge of the hidden variables, there is no need for any “spooky action,” as Einstein put it. The dial determines the spin of the atoms at separation. And any measurement of the spin simply determines where the dial was when they were separated. Simple, right? Not quite.

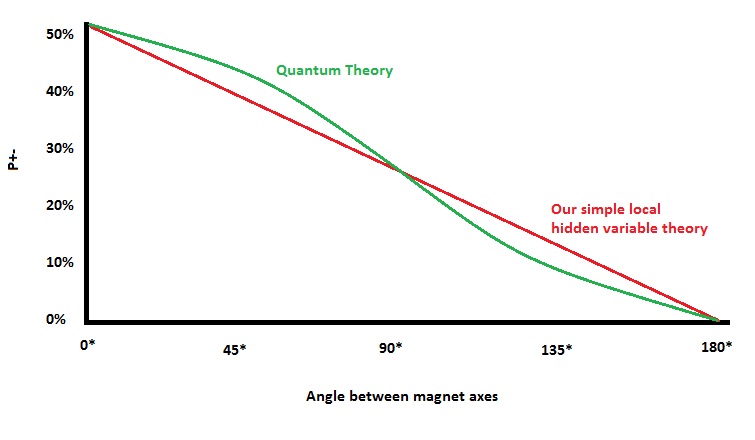
Bell took it a step further and began to calculate probabilities. If the magnetic fields are aligned for both detectors, we can say the probability for the dial to be in the top half of the dial face for Atom A is 50%. Because they have to have opposite spins, we can say the probability of Atom B’s dial to be in the bottom half is also 50%. We denote this as P+- = 50%. As long as the magnetic fields are aligned (as in Figure 20), we can also say P-+ = 50%. This is obvious as the top and bottom halves of the dial face each take up 50% of the total area. But what happens to this value if we rotate the magnets of the Atom B detector relative to Atom A’s detector? When you do this, what is considered the top half of the dial face rotates as well, changing the areas of each dial face half in relation to the dial. Because the dial is fixed into position, it means that the value of P+- will decrease as the angle of rotation increases. It’s easy to visualize if you think of the dial faces overlapping each other.
Consider Atom B at 45 degrees in the figure on the right. Superimpose it onto Atom A. You will see the area that the downward pointing dial can exist in has decreased. The beige colored top face is overlapping the bottom face. Remember that the dial is fixed into position – it cannot change. Do the same for 90 degrees, and you will see the area of the bottom face has decreased by exactly half. As the area decreases, the probability P+- decreases, and the probably of measuring both spins as spin up or “+” increases. With 180 degrees of rotation, probability P+- is at 0%. You now have P++, and we measure both spins as spin up.
A Simple Idea Gives Rise to the Bell Inequality
Quantum Theory gives the value of P+- as 1/2 cos2 (a/2) where a = the angle between the magnet axes. John Bell’s simple hidden variables theory agrees with quantum theory only at angles 0, 90 and 180 degrees, as seen in the graph below. However, considering how crude our theory is, the possibility should exist to make a more elaborate hidden variables experiment that would show that all angles would agree. Is it possible to do this?
After 17 years, John Bell realized that the answer was no, it is not. There is simply no way for any local hidden variables theory to account for all the predictions of quantum mechanics. He would go on to use a character by the name of Dr. Bertlmann, who had an unusual dress sense to eloquently describe his findings. And this will be the subject of part 2 of this post on Bertlmann’s Socks when all will be revealed, at least as much as is possible when it comes to Quantum Mechanics.
Sources:
The Quantum Story, by Jim Baggott. Chapter 31 ISBN-978-0199566846

















I just now am reading, “Time Reborn” and got thru a chapter on free-will vs hidden variables, and relativism and simultaneity. Hidden variables implies simultaneity which implies absolute motion which negates relative motion. Either we accept quantum (ie we always deal with probabilities) or we accept absolute motion which allows us to find hidden variables. The two are mutually exclusive. (And I hope I summarized that properly!)
..there is a deeper wave than this. all i can come up with..WAY above my uptake levels..
The problem I have with quantum mechanics is that most of it doesn’t pass my BS detector. I realize that I am apparently wrong and that much of it has been proven experimentally, but I just can’t wrap my head around some of the weirder theories.
I think that’s always the way with newly forming theories. Relativity is pretty easy to understand, but that’s only because it’s been filtering into general science education for half a century already. Try and find some talks on Quantum Mechanics at colleges in your area. Getting several different explanations can make the topic a lot easier to grasp (I avoid saying “a lot easier to understand” since I really don’t).
Except it’s not true that quantum mechanics is new compared to relativity–look at their histories, and you’ll find they developed at the same time. Bohr first proposed quantization in 1913. Einstein developed relativity between 1907 and 1915. Both worked from research done before them that was in active development up to their time. You might be able to argue (I’d say weakly) that relativity was accepted and taught earlier, but that’s about the best you could do.
I would imagine relativity is taught far more widely. We studied it in High School physics class but I don’t remember any teachings of Quantum Mechanics. Of course this is just one frame of reference.
I think the best way to learn Quantum Mechanics is to start with how it applies to chemistry. Valence shells, orbitals (which we’ve now been able to image!) and the rest of the “hows and whys” of chemistry rely on quantum mechanics or electrodynamics at some level. Once you can truly grasp that an electron is not actually orbiting the nucleus like a planet around a star but instead has a large percentage chance to be in it’s given orbit (as defined by Pauli, Born, Heisenberg, Schrodinger, et al) and a very small, but non-zero, chance of being somewhere else entirely; like the other side of the galaxy.
Once that becomes less frightening and something you can understand even if you can’t work out the maths yourself, then the rest of QM and QED start to become less scary. At least that’s my personal experience; I had all the strange voodoo ideas of QM from pop-science articles until I took Chem 101, 102, and Org Chem 101. Since the professor really liked the maths, he’d run through all the equations for finding where an electron could be during breaks in the class; and I took detailed notes so I could study them later. It wasn’t for any part of the tests, it was way beyond the scope of the class, but it helped out. As for why there were breaks in the class, it was a 5 week summer course, 4 nights a week for a few hours with a dinner break and then a break before the labs on lab nights.
That’s because people explain them in fantastic ways, because it makes them sound interesting. The truth is much, much more boring. “Wavefunctions collapsing instantly across the universe, faster than the speed of light!” sounds way more interesting than the actual truth.
For stuff like “wavefunction collapse” the easiest way to understand it is that it’s completely impossible to *measure* something without disturbing its state – which means talking about ‘measurements’ in some ways is confusing. You’re not “measuring” things that stay static. You’re interacting with the state, and inferring information about its state, but once an interaction happens, that state’s not the same anymore.
The non-existence of hidden variables leads to the conclusion that the property that is indetermined at any given moment does not actually exist until measured. The property is -added- upon measurement and removed again when that particular property isn’t involved in any interaction.
It’s actually meaningless to say that Alice’s atom is spin up because Bob’s atom turned out to be spin down, because from where Bob is the other atom doesn’t even exist until the information about it has propagated to Bob at the speed of light. At that point there’s another measurement, where Bob and Alice come together to measure each other and come to an agreement which of them actually had the spin up and down.
It makes sense if you think that nothing actually happened in the past, and everything is “happening” right now, right here. The information about what is and ever was is different in each point of space. If you step a foot to the left, your entire world would be different, but you would never know because you would be different with it. In all probability though, adjacent points wouldn’t be too dissimiliar because they’re likely to contain similiar information.
It’s the whole “doesn’t exist until measured” bit that hangs me up.
I understand that I am considerably ignorant about quantum mechanics, and I think I will stay that way in order to preserve what little I have left of my sanity.
Thanks for all the help, folks, but my brain just isn’t functional enough to get a good grasp on things like this. They don’t call me DainBramage for nothing. :D
Well, take two sticks and cross them. What do you have? A cross. Take the sticks apart – where does the cross go?
In a similiar way, when we measure something or interact with something, we combine what we are with what that is and in the process create other things, and when we stop interacting we retract ourselves from the equation and the things we created vanish.
The “doesn’t exist until measured” notion is misleading, in my opinion. The old idea was that we have innert matter and we act on it, but it’s more accurate to think of the world as full of active entities. There’s a lot of great philosophical work on this notion, see Jane Bennett’s Vibrant Matter http://www.dukeupress.edu/vibrant-matter and particularly Bruno Latour’s discussion of “actants”.
Latour is worth careful study, and would make for a great subject in a series of Hacking and Philosophy articles (as would Deleuze).
If you have a moment, take a look at Latour’s discussion of Pasteur and the discovery of yeast/fermentation. Think about it this way: did fermentation exist before it was discovered? (Latour would say “no”, but not because we now have a name for a process).
Contrasted the discovery of fermentation to the “2 sticks” example below–I would argue that the sticks –> cross is more of a social construct: coming up with a label (cross) to identify the thing (two sticks on top of one another). The discovery of fermentation, however, isn’t just a social construct. What Latour is trying to explain is that this yeast was changed by Pasteur, but also that Pasteur was changed by the ferment. It’s not merely this “thing” out there transformed by human intervention, it’s an event, with actants.
Latour defines an experiment as “an action performed by the scientist so that the nonhuman will be made to appear on its own…The experiment creates two narrative planes: one in which the narrator is active, and one in which the action is delegated to another character, a nonhuman one.” [1]
I would write more, but I’m pressed for time at the moment.
1. Bruno Latour, “Pasteur on Lactic Acid Yeast: A Partial Semiotic Analysis,” Configurations 1.1 (1993), John Hopkins UP, 142.
bruno-latour.fr/sites/default/files/51-PASTEUR-GB-pdf
“It’s the whole “doesn’t exist until measured” bit that hangs me up.”
Don’t say measured. It’s interactions that matter. Think about it this way. When people talk about an EPR experiment, they usually say:
“A spin-0 particle decays into two particles. Whatever the spin of one is, the other one has to have the opposite spin. They’re entangled. Now you let those particles propagate some far distance, and measure their spin. When two researchers compare notes on their measurements, they’ll find that their measurements correlate in such a way that cannot be explained by them having a definite spin state beforehand.”
There are lots of problems with this explanation.
1) How do you know the spin-0 particle decayed? Until you observe the pairs, you have no idea that it happened.
2) How do you know those particles are propagating over that distance in the meantime? To do that you have to verify the particle’s location. Which means you have to interact with it. Which disturbs its state.
In truth you *don’t* know any of those things that begin that last paragraph. That’s why you say “it doesn’t exist before it’s measured” – because *for this setup, you can’t do anything to actually verify it*. All you can actually say is:
“You prepare a spin-0 state, and isolate the future decay particles so they will interact with nothing else except a spin measurement. When they do interact, a correlation is found.”
This is why the distance bit is pointless – the decay particles aren’t *allowed*, by construction of the experiment, to interact with anything to establish their position. So what the heck does “position” mean? It doesn’t mean anything. If you isolate the system such that they can’t interact, you’re actually *observing the original particle*.
“Contrasted the discovery of fermentation to the “2 sticks” example below–I would argue that the sticks –> cross is more of a social construct: coming up with a label (cross) to identify the thing (two sticks on top of one another).”
Well, the stick can fit through a hole the diameter of the stick, whereas the cross will not because the cross-member would get stuck. The cross is a real thing with real properties that exist as long as the two sticks remain in that particular configuration. It’s not a “social construct”.
@Dax
I’m referring to the latter part of your response:
“In a similiar way, when we measure something or interact with something, we combine what we are with what that is and in the process create other things, and when we stop interacting we retract ourselves from the equation and the things we created vanish.”
That’s the social construct, and it demonstrates the differences between how we understand “interactions” as such. The cross example is passive–not really interactive at all–the person acts on the sticks. The yeast is a co-participant in the Pasteur example. I agree with you when you say “When we measure something or interact with something we combine what we are with what that is” but it works both ways — it combines itself with what we are, too.
I don’t intend for this to sound hooey or mystical. My point is that when we consider experiments from a “top-down” perspective of experimenter works on ___ and outputs ____, then we miss a lot of the nuance. Experiments are much more social (as in systems) in nature. They’re assemblages, and we should be much more aware of the relationships involved and how they work in both directions.
“”because from where Bob is the other atom doesn’t even exist until the information about it has propagated to Bob at the speed of light.””
I thought the point was that you could measure the spins anywhere you liked, whenever you liked and youd still get the same result.
I don’t think you have to wait for information propagation for one to be up and the other down.
At least, if it was the case that as soon as the property is added to Alice then B has to wait to “receive” the information, then you should get “uncorrelated” spins if you measure too quickly for that information to have propagated.
Additionally, If spin’s needed to wait for information traveling at C to be received, I don’t think Einstein would have tried so hard to make hidden variables work.
“I don’t think you have to wait for information propagation for one to be up and the other down.”
No, you’re misunderstanding. You can measure 1 spin “wherever”. You can measure the other spin “wherever” as well. But you will never discover the correlation between them until you bring the measurements together, which means that the idea that your measurement ’caused’ something to happen in the other particle is nuts. “Particles” don’t exist at all until they interact and leave a record of their existence, and when they do, it’s causal. It’s just a correlation – the measurements themselves don’t do anything causal.
It’s like a shadow on the moon. You shine a flashlight at the moon, and make a shadow puppet of a bunny dancing. An observer at one point sees a strange series of flashes. An observer at another point sees another strange series of flashes. You bring them together and discover “oh my goodness, a pattern!”
“Additionally, If spin’s needed to wait for information traveling at C to be received, I don’t think Einstein would have tried so hard to make hidden variables work.”
Einstein, like many physicists at the time, really didn’t like the idea that macroscopic ideas don’t really exist, except as probabilities (e.g. how much of the phase space is populated). They were very influenced by the idea of a clockwork-type universe, and the idea that it’s *literally impossible* to fully pin down the behavior of a system was really, really hard to integrate into their thinking.
“It makes sense if you think that nothing actually happened in the past, and everything is “happening” right now, right here.”
“It makes sense if you think that nothing actually happened in the past, and everything is “happening” right now, right here.”
This. This is exactly right.
This is in fact, is the entire point of relativity in some sense, which is why I always found it strange that Einstein had problems with this. “Now” for you is the exact same “now” as 1 light year away, 1 year ago. Why? Because information from anything more recent from that can’t have propagated to you.
In exactly the same way, when a spin-0 particle decays, if you make it such that neither of the decay particles interacts at *all*, then your measurement is exactly the same as interacting on the original state. It’s as if that state *just* decayed when you measured it. And since your measurement is *the first thing that indicates that it did decay,* well… in some sense, it *did*.
The best analog that I can come up with is still pretty terrible:
Imagine if there was some object, made of 2 mirrors, one of which reflects ‘blue’, and one of which reflects ‘red’ The mirrors are at right angles to each other: when you see ‘blue’ face on, the red mirror doesn’t do anything. Also imagine they’re weird mirrors – when they’re not face on, they reflect a non-linear portion of the light (e.g. at some angle theta, they reflect f(theta)). I dunno, you can probable build something like this. Now imagine that object was spinning wildly such that its orientation was totally random from one moment to the next.
Now imagine you don’t know they’re at right angles. So how do you figure out the relative orientation of the red/blue faces? You shine a light on it, and you measure the amount that reflects back. But you’re only allowed to shine one color. So when you shine the red one, you find out its orientation… but you have no idea what the blue one was. Hm.
So you get a friend, to shine a blue light on it. And now you’re super-careful, and make sure that your light pulses arrive at *exactly the same time*. So you can measure both of them. And when you do that, and correlate all of your measurements, you say “huh, they’re at right angles.”
That’s exactly the same math as an EPR experiment. And it doesn’t seem confusing at all. You don’t worry about the wavefunction of the spinning object collapsing. If you put your ‘blue laser’ friend on the Moon, you don’t say “oh my goodness, his measurement changed the instant I got my pulse back.” Of course not – that would be stupid, because your pulses arrived at the exact same time. So your measurement of the spinning object occurred at exactly the same time.
And that’s the point. If you isolate a system such that its decay particles don’t interact with *anything* else (more precisely, so its spin state stays undisturbed) *you’re still measuring that original state*. The “position” or “time” doesn’t matter, because, to those particles… it still *is* that same original time. Nothing happened since then.
This is quantum mechanics answering the “if a tree falls in the woods, does it make a sound” question. The answer is “no.” If it leaves no trace, it doesn’t exist.
I thjink it is because pop-scitech writers are very eager to present quantum theories as if they apply to normal perception directly metaphorically to how it works on quantum scales.
So people go around saying that we “live in a hologram” and that “nothing is real”, etc… With no philosophical or logical basis, but every pretention of such basis.
As a great intro to the subject, please allow me to recommend two books (read them in order) that I found very enlightening when I was first trying to grasp anything at all about quantum mechanics:
First: “In Search of Schrödinger’s Cat: Quantum Physics and Reality” by John Gribbin (http://amzn.com/0553342533/?tag=bestbookchoices-20)
Second: “Schrodinger’s Kittens and the Search for Reality: Solving the Quantum Mysteries” by John Gribbin (http://amzn.com/0316328197/?tag=bestbookchoices-20)
From there some of the headier material becomes much easier to approach. Gribbin’s a great author who does a solid job of bringing these concepts within reach of even skulls full of mush such as myself. Can’t recommend them enough!
I’ll second Shrodinger’s Kittens and the Search for Reality. Really easy to understand and pretty light on the math if I remember right; relying more on “this is why it is and if you want the equation here’s a text book you can read”.
One of the reasons for this is that quantum effects are difficult (for your average person) to touch experimentally. I don’t have access to the equipment to run, say, a double-slit experiment or measure the spin on a hydrogen atom.
But there is one experiment the average person CAN do – and I carry it in my wallet.
I purchased some polarised plastic film from some web-site and cut out 3 squares. I get two of these squares and look through them whilst rotating them with respect to each other. At alternating 90 degree positions I can see through vs. they are completely black. All good – this is how I expect polarised film to work. Then, with the two squares positioned so they pass no light, I insert the 3rd square between them at 45 degrees. Now some light gets through.
I love the fact I can show anyone a quantum effect in less than a minute. The downside is that most often I get asked “how does it work?” and I stumble thru an explanation. They are none the wiser, but I’m getting better at understanding it!
Note: this is not a good way to pick-up chicks in a bar.
That’s awesome. *runs to grab 3 sets of 3D glasses*
Polarization filters for cameras are probably cheaper. Sometimes they show up in sets for three different lens sizes; instant experiment!
Wrong kinds of women? I would have fallen for that prior to understanding it, and showed my MIT student cousin the effect and had a long conversation about it (she wasn’t studying physics, bio-chem I think). Another good one is showing how stretched pieces of scotch tape take on color under polarization. Use that to create pictures, or “what do you see in this invisible cloud”. Only works on the geeky, who may not be hanging out at bars.
And you can explain it as “very thin Venetian blinds”. That was the description Professor Nagle used in the demo of the effect to young children; and it’s true. Thin, in this case, just means on the level of nanometers.
You, sir, just won the internet for today.
Just show someone the effect of Saccades, most people aren’t aware that you cannot see your own eyes move in a mirror. But watch another person moving their eye sight from one eye to the other in a mirror, you can see them move, while the they cannot.
Basically, brain takes a snapshot, the eyes move, vision is cut off, eyes stop moving, snapshot is reloaded, return to realtime vision. Yes your reality breaks.
It doesn’t pass anybody’s BS detector. That is what makes it so hard. It is the most accurate and precise theory ever created to describe/predict the way nature works. But it is so unlike daily experience that it requires a language of mathematics that makes General Relativity look simple – which it is, being linear when you get local enough. Try that with QM and it will not play. You have to trust the math – very much like a pilot with vertigo has to concentrate on and trust the instruments in the plane. The result though is predictions that prove correct to a lot more decimal places than we know the gravitational constant. (Also, like the “twin paradox” in GR, a lot of things the science writers term paradoxes are not. They are just a little more complicated to explain. They like to simplify. Like the description here that doesn’t mention the high field strength gradient required for the Stern-Gerlach Experiment. A uniform field would do nothing.)
Now, I recall Stimpy found where all those missing socks go. I hope there are some details on that!
No way. Not for this concept.
It really, really doesn’t require super-complicated math. For one thing, it’s all linear algebra, and for crying out loud, GR is tensor calculus. Basic quantum mechanics is high school math. It requires one change in your thinking, and to be honest, it’s not even hard to get there. (Quantum field theory is a lot freaking harder, sure, and I’ll agree that it’s harder than GR in terms of math, because we literally do not have the math to describe it well.)
What’s that change in thinking? Remember the second law of thermodynamics? Entropy always increases. This is sometimes called “the arrow of time.” This is how you define causality. If the entropy of an isolated system is higher, it’s “later in time.” If the entropy of the system is lower, it’s “earlier in time.” If it’s the *same*, it’s *exactly the same time*. There is no other measure of time than entropy.
People struggle with that concept for a while, but it’s not that far away from your experience. You can’t make anything last forever. Everything decays.
Here’s the change in thinking: entropy is information. Entropy is the Universe telling you “hey, something happened.” That piece of iron rusted because *things happened to it*, and you can’t “undo” the fact that things happened. So entropy always increases. So you can say “entropy is the collection of interactions that have happened.”
So now apply “entropy is information” to “entropy is the arrow of time,” and your result? If no interactions happen, no time passes. And suddenly all of the spooky action-at-a-distance stuff goes away. Those decay particles didn’t interact. So no time passed since it decayed.
Then how does entropy increase from big bang inflation? How can it possibly be increasing ?
I don’t understand your confusion: entropy increasing just means “things have happened.” Obviously things have happened since the Big Bang.
Questions regarding “total” entropy of the Universe are a little esoteric, since only a small fraction is observable to us.
So your question *might* be “how does the entropy of the entire Universe increase, when it’s a closed system?”
In fact, we know the *observable* Universe (stars, planets, gas, etc.) isn’t a closed system at all. That’s what the Big Bang, and the cosmic microwave background tell us. Both the Big Bang and the CMB are ‘universal reference frames’ – everyone can go to the rest frame of the CMB, or the rest frame of the Hubble flow, and those are special reference frames. And a special reference frame means violation of conservation of energy: both the CMB and the Big Bang *injected energy into the Universe*.
This is well accepted, but we have no idea where that energy comes from. So cosmologists invented a field to be a simple model for how inflation might have occurred (the ‘inflaton field’) – and so for inflation, that’s where the energy (and entropy) came from – the massive reduction in number of available states of whatever caused inflation. Something similar must have happened for the Big Bang, but obviously we have even less information than for the CMB, so there aren’t even really ‘standard models’ for that.
There are actually even more examples than that on a local basis, in the sense that if you calculate the entropy of a galaxy, for instance, right after inflation it started *decreasing* as the gas clouds collapsed much faster, and large-scale structure formed much faster and bigger than you’d expect. And that’s coming from dark matter. So again, it’s the same thing – something unknown (dark matter) is losing entropy, decreasing its information content (how many states are available in the system) and transferring that to the *observable* Universe – us.
Or the laws of entropy/quantum change over time. I think this is what the “time reborn” book suggests.
That’s identical, for the most part. It’s less helpful to think of it that way, though. Just having time-variant laws of physics isn’t really building a model – it’s just fitting data. You can’t predict anything more. If you instead say “there’s an inflaton field, some potential that breaks symmetry, and this is what you get” then you have testable predictions.
I mean, that’s why theorists keep working at explaining the Big Bang rather than just saying “it happened” – they’re looking for side effects that could result in testable models. Anything other than that is just philosophy.
Ok. And just something to note: the “time reborn” book does suggest testable theories. That is the point of the book. Supernova that collapse should make neutron stars less than such and such a mass in order for some of the time variant theories to hold. Not just fitting data.
The theories might not be correct in the book but they are testable in this unique/single universe. (Ie no other universes to act as control variables).
No, I think you’re misunderstanding: saying “hey, it’s possible that physics might change over time” is fine. But even observing a change over time would just be an empirical observation, not a useful model. The idea that the laws of physics are static is a *choice* that physicists make, not some basic underpinning of the Universe. (Which was a main part of Smolin’s book as well). Unless you can come up with an explanation as to *why* that makes it easier to explain observed results, it’s not useful.
For instance: you can actually replace the entire idea of an expanding Universe with the idea that gravity has been getting weaker over time. Dirac suggested that a long time ago. But that observation is pointless – it doesn’t simplify anything, and doesn’t predict anything new either.
But, in fact, recently someone pointed out (here) that you could explain an apparent expanding Universe, inflation, and get rid of the Big Bang all with the idea that the *mass* of everything in the Universe has been increasing over time (thus the gravitational attraction has actually been shrinking over time to keep things constant). And you could imagine doing all that by coupling a scalar field (a new particle) to gravity. Poof.
And *now* that becomes a useful idea, and might have predictable observations, or might make existing observations simpler to explain. Right now, the two models – static universe, growing masses vs. expanding universe, static masses – are completely identical. They predict exactly identical results. To quote the author:
“Our model should be interpreted as a new complementary picture of cosmology, not as opposing the more standard picture of an expanding universe. The different pictures are equivalent, describing the same physics.”
A very similar discussion on this topic is here.
I should also point out that you literally can’t say “the laws of entropy change over time.” They can’t. Like Newton’s second law, they’re ‘laws’ because they’re actually definitions. They literally cannot be wrong. Entropy is just a statistical description of the number of states and their likelihood.
Likewise, stating that “the entropy of a closed system increases” really in some way can be used to *define* the direction of time. There isn’t anything else in physics that does it otherwise.
There are a lot of quantum quacks out there, but as to the real science, Feynman says it best:
https://www.youtube.com/watch?v=_sAfUpGmnm4
Quoting Richard Feynman (famous theoretical physicist) “If you think you understand quantum mechanics, you don’t understand quantum mechanics.”. All top experts in quantum mechanics seem to agree they don’t really understand it! The mathematical formalism is well understood (and predicts reality accurately) but no one can really figure out what the heck is going on. So don’t fell bad about not understanding it… no one really does! ;-)
“All I know is that I know nothing.”
Love this kind of articles, thanks a lot!
I like the article, but boy is it a tease. Part 2 please!
I will just leave this link in here, for those who are interested: http://lesswrong.com/lw/r5/the_quantum_physics_sequence/
Classic documentary on the topic:
https://www.youtube.com/watch?v=BFvJOZ51tmc
Wow. Watching this in 2021 — they have interviews with some _really_ heavy hitters in Physics. Bohm commenting on Bell, with anecdotes from Wheeler… holy cow!
Mosr physics posts pleeze. Less contest posts pleeze.
i remember Prof. Lerner saying what you’re really measuring is “THE PROBABILITIES WAVING ..” and that “Theories ” such as String Theory are “perfectly preserved”,because they could never be tested.. Wish i could just grasp alittle bit of it..you students of today will probably make some of the greatest discoveries yet, possibly the greatest ever..at the crossroads of consciousness and reality.
Q on Schrodinger’s Cat Experiment . I realize this is probably a dumb question but I’m going to ask anyway because I’m both fascinated and curious about QM.
The classical argument is that the cat is both dead and alive until we open the box (until an observation of the cat is made) . If the box is air tight and there is enough oxygen in the box for the cat to survive for 1 hour then if we open the box at the 30 minute mark, measuring the level of oxygen just prior to opening the box, then if the level of oxygen in the box is at or near the same level as when we started doesn’t that prove that the cat was not alive but dead?
If the cat is dead and alive until observed then one could argue it has both consumed the oxygen and not consumed the oxygen so if when we open the box and the cat is alive the level of oxygen measured in the box supports what we have observed; that the cat is alive. It also means that it could have been dead and alive until we opened the box, If however the cat is dead when we open the box and the level of oxygen measured is at or near to what it was when we started then doesn’t that make it impossible for the cat to have been in both states until we opened the box and observed the cats state?
Thanks
As I understand it, the act of measuring would, in itself, be the determiner of the quantum state. Because the cat is in a superposition of states (both dead and alive until measured), so too is the oxygen quantity in a superposition of states (it is both rich and thin). In essence they are tied to each other, not quite at the level of entanglement, but certainly in a dependent fashion.
Note: there’s a significant chance I may have that entirely wrong… it’s been several years since I read through “Schroedinger’s Kittens”.
This is the problem with people giving analogies for quantum mechanics concepts. They’re all poor analogies.
“The classical argument is that the cat is both dead and alive until we open the box”
Yes. Because it’s a magic box. It’s a magic box that prevents you from finding out, from any way, from the outside, if the cat has died. “Opening the box” and making the observation is a terrible way to describe it. That’s not the important point.
Think of it like “trapping the information as to when the cat died.” That box has to prevent *all* information regarding the cat’s state from getting out. All of it. Heat, light, sound, chemical energy, potential energy, kinetic energy… *everything*. If that information can be trapped completely inside the box, then *from the outside world’s point of view*, it’s in a mixed state.
“then if we open the box at the 30 minute mark, measuring the level of oxygen just prior to opening the box, then if the level of oxygen in the box is at or near the same level as when we started doesn’t that prove that the cat was not alive but dead?”
Yup. But the point that you’re misunderstanding is that from *the cat’s* point of view, it was never in a ‘mixed state.’ It was always alive or dead. Of course the cat died at some specific time, and once you open the box, you can do any sort of tests you want to figure out when the cat died. That part isn’t important.
The important part is that *until* you open the box – because it’s magic – there’s absolutely no way for you to know what the state of the box is. So you have to consider that it’s in a mixed state.
The thing is, this effect has absolutely no practical effects. From *the cat’s* point of view, it’s not in a mixed state. The cat’s body encodes information – so it can store the information as to when it died. From the outside world’s point of view, there’s no difference between saying “It’s in a mixed state” and “I don’t know if it’s dead” because the only real difference would be finding a way to interfere that mixed state with another one, and there’s no way to do that.
So it’s really not that interesting a thought experiment at all, except to make you realize that when you talk about a mixed state, you’re talking about a state that has been prevented from interacting with the Universe as a whole.