Would you believe a pendulum clock that can keep time accurately to within one second per year? If you answered “yes”, you’ve either never tried to regulate a pendulum clock yourself, or you already know about the Shortt Clock. Getting an electromechanical device to behave so well, ticking accurately to within 0.03 parts per million, is no mean feat, and the Shortt clock was the first timekeeping device that actually behaves more regularly than the Earth itself.
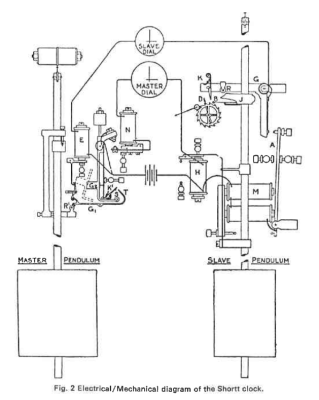[Matt Little] passed us this link to an interesting technical writeup (PDF) of the clock. The trick behind the most accurate pendulum clock is that it actually has two pendulums (pendula?). One, enclosed in a metal cylinder held at a decent vacuum, keeps time but doesn’t do any mechanical work at all. Instead, through a series of mechanisms that are designed to alter the pendulum’s swing as little as possible, it sends an electrical signal every 30 seconds and kicks the slave clock which is purposely designed to run a little bit slowly. The slave clock is then free to do heavy lifting like move clock hands.
The cool part of the article comes when the author gets to shine a light on a mirror on the master pendulum, and compare its behavior to modern ultra-high precision clock sources. There’s a lot of what looks to be random noise in the clock’s periodicity, but the biggest contributors turn out to have physical origins: the tidal pull of the moon (obvious) and the sun (what?) change the local gravity enough to leave their mark.
If you can’t get enough Shortt clocks, look at the Wikipedia entry on the device, or check out this private collector’s website for pretty pictures, including the one used in the banner image. Or if your tastes run more toward the modern cyberpunk atomic clock, we’ll just leave this link here.
1 second per year is really good for an oscillator of any kind. If you want a crystal oscillator to be that stable, you have to put it in a precisely controlled oven.
Note many modern RTC chips already include a built in software count compensator for off-spec crystals:
https://www.microchip.com/wwwproducts/en/MCP79412
(very handy if you traditionally had to keep 15 spools of 4pF to 30pF values around to tune your ageing clock inventory)
As long as the fundamental frequency is stable (no physical/thermal shock or x-ray damage), the ageing drift has actually been modelled by some to predict how the crystal will change over time. Thus, an inexpensive clock can remain very accurate even as the oscillator slowly changes. As a side note, I have not witnessed any appreciable correlation between the ppm rating of modern crystals, and the rate of accuracy drift over time. However, using good quality pure ceramic 5% capacitors does seem to improve the drift profile, as a change from 1.3s to 7s a year is negligible to most users.
Oven controlled crystals can also drift over time (usually have an adjustment screw or pin on the can), but are much more stable in operation once warmed up. The people serious about SDR should always try to get a double oven stabilized 10.000000MHz reference for their equipment.
I’m a big fan (no surprise) of GPSDOs. A nice OCXO for short tau stability combined with the spectacular long tau performance of GPS – best of both worlds.
You have to do even better than use a precisely-controlled oven, because quartz crystals age over time, in an unpredictable manner.
Please read this Jim:
http://www.isotemp.com/wp-content/uploads/2011/04/Crystal-Oscillator-Aging.pdf
Old people usually know a lot about time…. =)
Today we has temperature compensated crystal oscillators (TCXO).
The temperature drift of a crystal is easily calculated and compensated for and this is much easier to do than a complex and power hungry oven setup.
The DS3232 real time clock chip (RTC) has an inbuilt TXCO.
TCXOs just aren’t going to be as good as OCXOs. I’ve used both in my GPSDO designs, and the OCXOs I use are almost an order of magnitude more stable at short tau (at long tau GPS discipline moots everything).
Horses for courses. A lot of devices can’t afford the power budget of a OCXO.
THAT is certainly true. My OCXO model needs 5 watts. The TCXO model barely needs one.
That’s cool, effectively a PLL.
>”and the sun (what?) ”
The sun makes the tides stronger and weaker according to the phase of the moon, or whether the moon is in front or behind the earth. Their gravitational pull adds up.
The moon tides I totally buy, and the fact that they’re stronger or weaker depending on whether they align with the sun’s (roughly constant) pull. The earth is pretty big, and we’re not all that far away from the moon, so the difference in gravity on one side and the other is fairly large.
But to detect the difference being on one side of the earth or the other with respect to the Sun? It’s hella far away. (Approximately one astronomical unit.) The width of the earth is a lot smaller in that comparison. I’m still impressed.
Hella far away, but also hella bigger (and, more importantly – a lot heavier)… Look up some tidal forces basic, you’ll be surprised on how much of a difference it can make.
Apparently the gravity force between the sun and this planet is big enouh too keep it running in circles.
Apart from that, this force changes with distance (eliptical orbit).
But more: at night the resulting gravity is bigger then average, and during the (each!) day it’s less than average.
For some math: Multiply both masses, divide by distance (squared?) and add a bit of gooey stuff.
The highest gravity one could experience on Earth would be to stand atop Chimborazo at midnight during a New Moon.
That puts the the most mass between you and the center of Earth, plus the mass from the center to the other side of Earth, and the Moon in line between you and the Sun.
The least gravity you could experience on Earth would be to stand beside the Dead Sea at noon during a New Moon. The would give you the least mass below your feet to pull down on you, plus the upward pull from the Moon and Sun.
I wonder how much difference there would be in effective gravitational pull between the two locations and times?
It’s more complicated than you both make it out:
Have a look at the tides: being on the moon’s side (and the sun’s side) rises the tide — the sea is “lighter”, that is somewhat obvious. The biggest effect is to be had with new moon at noon. So far so good. But… the antipodes (midnight, new moon) are experiencing a (pretty high) high tide too! WTF?
The ones with low tides at this moment are those “at the sides” (dawn & dusk, so to speak).
The thing is that the tidal “forces” (and this is what’s influencing a pendulum too) are a differencial between gravitation (Sun’s, Moon’s) and centrifugal (that of the orbit around the Sun and that of the orbit around Earth’s and Moon’s common center of gravity).
Yeah “mumble mumble common” is also valid for Sun–Earh.
And then there’s Coriolis…
Wouldn’t you want to stand at the lowest elevation possible, to be closer to the center of the earth? I’m pretty sure that when you stand on top of a mountain, you actually weigh LESS. That’s because the earth’s mass is not evenly distributed, so being on top of a mountain is more or less the same as being in an airplane. It’s possible you could even fiend some area on the equator that is located above and unusually dense section of the planet; that would probably be the spot to go for highest gravity, regardless of elevation. There are maps of such gravitational anomalies, created using satellites.
Is it a matter of the increased distance, being on one side of the Earth or the other? I’d expect it’s more to do with the direction. On one side, the Sun’s pulling up, towards the sky. The other side, it’s pulling down toward the ground. So it’s not the distance across the Earth that matters, it’s the gravitational pull of the entire Sun.
I had an ‘aha’ moment at the Monterrey Aquarium a long time ago. They had a chart recorder showing the heights of the tide over several months’ time. You could see the for MOST of the month there were two tides per day, but their phase relationship shifted over the month, getting closer and closer together until they overlapped and made an extra-high tide. They then diverged from there. The full cycle was about 28 days, so while one of the tides was happening 28 times, the other was only 27. Or it may have been 29 and 28 respectively – that was a long time ago. My guess was (and is, since nobody has corrected me on this (yet)), that one of these tides is predominantly due to the Lunar pull, while the other was due to Solar pull.
I further guess that the fact that both of these tides are about the same amplitude is similar to why both the Sun and Moon have nearly equal apparent diameters as viewed from the surface of Earth – sure the Sun is much farther away, but its much greater mass makes up for it.
https://en.m.wikipedia.org/wiki/King_tide
[Bob] Thanks, I think. Since all you did was link an article, I can’t tell if you’re trying to set me straight or confirm my guesses. The article seems to confirm.
The reason I brought this up in the first place, which I probably should’ve stated, was that I remember being taught in school that the tides were caused by the moon alone, and that the two-tides-a-day thing was caused by lunar gravitational force alone that formed bulges on both sides of Earth, by some logic that I couldn’t really follow. The explanation that went along with this didn’t sit well with me, since it didn’t explain why there were was a predictable cycle of higher and lower tides throughout the month.
usually a RETROTECHTACULAR is a video showing something by the government so where is the video?
> Usually
> Usually
> Usually
(PDF) Retrotechtacular!
Sorry to mislead. But a video of a pendulum clock doing its thing…. would actually probably be neat in this case.
No links in the main page now? What are you trying?
No.
According to the Wikipedia article on the Shortt clock, the 1 second/year measurement was incorrect, in that it didn’t take into account the tidal forces. A more modern measurement (1984) came to 1 second in 12 years.
Correction: the earlier measurement’s inaccuracy had nothing to do with tidal forces, but was due to the fact that there wasn’t anything more accurate to measure it against, other than the Earth’s rotation. The 1984 measurement was against a collection of Cesium beam clocks.
Last week, I visited the Royal Observatory at Greenwich (in London, UK) to see the Burgess ‘B’ clock. This is a modern clock which has now been certified, after lengthy testing, to hold an accuracy of better than 1 second in 100 days – in free air – (in other words, unlike the Shortt clock, it does not operate in a vacuum, so it is exposed to normal atmospheric conditions). That is better than 0.1PPM accuracy. Checkout http://leapsecond.com/pend/clockb/ and http://www.frodsham.com/burgess-regulator/
The Shortt clock was made for observatories which required an ultimate time standard, in the days before atomic clocks. There were others, like the Riefler and the Fedchenko, but, like the Shortt, their pendulums swung in a vacuum. The Burgess B is a fine clock to look at, whereas the others are not designed to appeal to the eye, as they were usually kept in a deep basement where the environment could be controlled. They were master clocks, so the slave would be nearer the humans standing at their telescopes or wherever. To a mechanical afficionado, they are, of course, things of beauty.
The Royal Observatory has examples of them all, as well as many others. Worth a visit if you like clocks.
I have been to Greenwich too, fascinating stuff. The work that Harrison, Shortt and everyone else did on timekeeping, long before the age of semiconductors was truly incredible. We stand on the shoulders of giants, and often don’t even realise it.
The linked article is now behind a NAWCC paywall, and a clumsy one at that, because you can’t buy just the article. A shame, because I had read it years ago, and wanted to see the tidal data again. Does anyone have a copy to share?