If you have more than a few bank cards, door-entry keycodes, or other small numeric passwords to remember, it eventually gets to be a hassle. The worst, for me, is a bank card for a business account that I use once in a blue moon. I probably used it eight times in five years, and then they gave me a new card with a new PIN. Sigh.
How would a normal person cope with a proliferation of PINs? They’d write down the numbers on a piece of paper and keep it in their wallet. We all know how that ends, right? A lost wallet and multiple empty bank accounts. How would a hacker handle it? Write each number down on the card itself, but encrypted, naturally, with the only unbreakable encryption scheme there is out there: the one-time pad (OTP).
The OTP is an odd duck among encryption methods. They’re meant to be decrypted in your head, but as long as the secret key remains safe, they’re rock solid. If you’ve ever tried to code up the s-boxes and all that adding, shifting, and mixing that goes on with a normal encryption method, OTPs are refreshingly simple. The tradeoff is a “long” key, but an OTP is absolutely perfect for encrypting your PINs.
The first part of this article appears to be the friendly “life-hack” pablum that you’ll get elsewhere, but don’t despair, it’s also a back-door introduction to the OTP. The second half dives into the one-time pad with some deep crypto intuition, some friendly math, and hopefully a convincing argument that writing down your encrypted PINs is the right thing to do. Along the way, I list the three things you can do wrong when implementing an OTP. (And none of them will shock you!) But in the end, my PIN encryption solution will break one of the three, and remain nonetheless sound. Curious yet? Read on.
The PIN Solution
So first the solution to the bank card problem: write your PIN encrypted with a secret that only you know. Instead of needing to remember a four-digit number for each new card, you’ll just need one four-digit number forever. The key is to choose an encryption scheme that’s easy enough to undo so that you won’t look too strange when asked to type the PIN in at the bank teller’s window. This is the classic use of the OTP — an encryption that you can undo in your head.
First, randomly select a secret four-digit number. Then, subtract that number from your PIN and write the result on your card. To get your PIN, when standing in front of the bank teller, simply look down at the card and add the secret number back. The teller will think that you’ve written your PIN on the card. Feel free to feel smug, because you’ve used an unbreakable encryption scheme.
Instead of normal addition and subtraction, with the carrying and borrowing across digits, you will want to use modulo-10 math — adding or subtracting ten from the result any time it gets outside the range 0-9. We’ll talk about why below, but for now, here’s a working example.
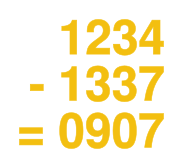Suppose the PIN is 1234 — it has to happen so someone, right? — and my random secret number is 1337, naturally. Let’s encrypt. Subtracting 1 from 1 gives a zero, so I write that down. Subtracting 3 from 2 gives -1, which is where the modulo-10 arithmetic comes in. In this case, -1 turns into 9 by adding ten. 3 – 3 = 0, and 4 – 7 = 7, mod-10. My card now has 0907 written on it.
Now let’s decrypt. Looking down at the card, I see a 0 and add 1. 9 + 3 = 12, however, so we’ll need to subtract ten to get 2. (That’s the reason to choose addition for the decryption stage, it’s easy to just drop any leading 1s.) 0 + 3 = 3 and 7 + 7 = 14 -> 4<. I type in 1234, and the money is mine!
Once you get the hang of adding your secret number to any other number, digit-wise mod-10, you’ll be surprised how quickly it will work. Try it out and see if you get good at it within ten minutes.
One-Time Pads
A one-time pad is both the simplest symmetric encryption scheme and also completely unbreakable. It has three crucial features, two of which were demonstrated above, and getting any of them wrong can be catastrophic.
The most important feature of an OTP is that the password needs to be random, and the same length as the text that it encrypts — hence the four-digit secret for the PIN. In an OTP, everything revolves around the secret, which is also its Achilles’ heel. For a four-digit number, keeping a four-digit secret is no problem. But imagine that you want to send gigabytes of encrypted photos of your vacation to a friend. That’s a lot of key material to keep on-hand and secret.
Third, and maybe this is a corollary of the first, you shouldn’t re-use the secret in a one-time pad. You’d think that this was obvious, since it’s even in the name of the encryption method, but it’s hard to do in practice. And in fact, my PIN-encryption scheme breaks this rule by using the same secret across multiple keys. We’ll get into that soon.
Messing up the Perfect Encryption
Why is a OTP unbreakable? Breaking most encryption schemes often boils down to probability and statistics. For instance, if you encrypt a text with the Caesar cipher above, each letter in the plaintext is mapped to another single letter every time it occurs in the ciphertext. If you know that the original text is in English, where the most commonly used letter is “e”, it’s a good bet that if “q” is the most common letter in the ciphertext, it stands for “e”. That is, we find statistical similarities between the plaintext and the ciphertext, and use them to make a bridge between the two.
Using a secret key that is as long as the plaintext, and randomly chosen, breaks any statistical relationship with the ciphertext. Given a specific ciphertext written down on my card, every PIN from 0000 to 9999 is possible, and if the key was chosen randomly, is equally likely. There is no information about the plaintext in the ciphertext — that’s essentially Claude Shannon’s proof (absolutely classic PDF) in a nutshell. And that’s why an OTP is unbreakable.
With that in mind, you can screw up an OTP implementation by using a short or non-random password. Imagine using 1 as your password and repeating it as necessary; our ciphertext would read 2345, and the PIN would be guessed on the second try. You also want to use a random password; picking 0000 because it makes the math easy is the only thing worse than the above. (Although, strictly speaking, I’d re-roll if I got 0000, 1111, 9999, 1234, 4321, or similar.) Anyway, don’t use your birthday. Old phone numbers of childhood friends might be acceptable.
The role of modulo arithmetic is a little more subtle. Whatever function is used, the set of possible characters in the plaintext has to map one-to-one with the ciphertext. Why? Imagine that you used simple addition instead of mod-10 addition. To get the last digit of our PIN ciphertext, we used 4 – 7 = -3 -> 7 and decrypted with 7 + 7 = 14 -> 4. If we wrote down -3 instead, an attacker would know that our last digit couldn’t be greater than 6 because adding 9, the maximum value, gives only 6. We’ve leaked information by having a larger set in the ciphertext than in the plaintext.
And that leaves the last way to mess up: re-using the “one-time” pad. Obvious, right? Wrong.
On one hand, reuse is a definite liability. Re-using a password in a very similar encryption scheme broke “Tunny”, an important code during WWII. A 4,000 character encrypted message was sent but not received correctly. The sender re-sent the message, with the same secret but made small changes in the text, using different abbreviations and so on. This gave the Allies enough to break Tunny and reverse engineer the machine that encrypted it. Game over.
Here’s the math that made the Tunny decrypt work, and should convince you to almost never reuse a key. If we encode the messages A and B with the secret key C, and someone overhears both, they can just mod them together to get (A mod C) mod (B mod C) = (A mod B) mod C mod C = A mod B, where mod is the bitwise or number-wise modulo operator that we’re now used to. Since taking the binary modulo is its own reverse, the result is something that’s related to both plaintexts, and independent of the secret key.
From here, comparing smart guesses for A and B and comparing them with the A mod B result can break the code. So if you’re pretty sure that “attack” appears in both texts (crypto types always encrypt “attack at dawn”), then you can try modding “attack” together in different positions until you get a match with A mod B.
A Surprise Ending
But here’s the final twist! We can get away with reusing the secret key across all of our bank cards, even despite the above math. Why? Because the PINs themselves are random. In contrast to the natural-language messages sent during wartime, A mod B is just as random as A mod C if both A and B are random PINs.
So this is how a hacker remembers PINs: by learning a lot about the one-time pad, how to break it, and how it’s nonetheless useful if the message it needs to protect is short. And how, for particular messages, you can even break the rules.
Wow, now this is a cool post. Great explanation; I can actually see myself using this. OTPs have always fascinated me, but their limitations always made them unusable for my own circumstances. Finally a valid use case!
This breaks if one of your cards has been caught in a tampered ATM with a video recorder – the video sees the written pin, and the entered pin. Now they can extract your “secret” and now your other cards are all compromised. This is exactly why it’s meant to be a “one” time pad. It’s not much better than simply changing the pin on all your cards to being the same.
No, it won’t work that way. If a hacker have compromised an ATM, he will not even need to record your card, ATM already recorded all data he will need: the magstripe data and your PIN. Anything written in the card isn’t needed.
Even if he recorded the PIN and the key, he would need to correlate the key to you, and to all cards you have. He would use an ATM with a camera to do that, right? And we are back to the previous step: the hacker will have the magstripe data, the PIN, and will not need anything else.
For that one card. Having the image of your written pin and the pin entered to the ATM he can then compromise any other cards that use that common OTP.
The point is, if he has your real PIN, and sees the number you’ve written on your card, a simple subtraction then gives your secret number.
With the secret number, he just needs to add the numbers you’ve written on each of your other cards, and he has the PIN for every one of them. Hence why you shouldn’t re-use keys, in this case. And the same reason in general for passwords etc.
Personally I remember my PIN using the letters on the keys, and remember it as something alphabetic. A word or part of word, or abbreviation or name.
The most common way to compromise an ATM is with a skimmer device, not a direct ATM software hack.
The skimmer device probably has a camera to capture the PIN and/or the verification code on the back of the card (which I don’t think is recorded on the mag stripe, but I’m not 100% sure).
But it’s exceedingly unlikely they’ll bother to reverse-engineer your PIN obfuscation scheme in any case – there’s no benefit to them unless they know your other card details.
True. A skimmer would want the numbers that he/she can use over the phone / on the internet. In that case the skimmer only needs the number, name and verification code. Probably all viewable from the back side with a decent camera – no need to even see the front with many cards (the imprint of the front name/number goes all the way through).
They don’t need your PIN, which is only of use with physical access. When did your card last get ‘swallowed’ – you’d be pretty sus if it did!
Plus, if they have a skimmer on an active ATM, why would they bother doing all that work for your other accounts, when they have 50 other cards, with PINs, without any additional effort? They will drain your first account, and the rest will be drained next time you use them at a different ATM with a skimmer.
“It’s not much better than simply changing the pin on all your cards to being the same.”
Thanks for this comment I was wondering here…. ok not so secure but using same pin an all cards was looking like not a so bad solution … (it is in theory but piratically… —> your conclusion)
True, but a bit more complex than that. This attack breaks everything only if:
1.) A photographic record of your written key is available and usable.
2.) The bad guys are looking for the article’s type of key and understand what they have when they see it.
3.) The bad guys have access to all your other cards/accounts and are interested in cracking all your PINs rather than some broader money harvesting method.
The first of these fails easily – writing the number along the top of the card ensures that the reader’s carrier rails generally obscure anything written there, as will the hand that puts it into the machine (we won’t get into the low resolution cameras usually used for this). You can argue the reductio ad infinitum case of putting a linear scanner in the rails or similar, but I’m not going to worry about it. Also I’d (almost) be happy to give “them” the key directly given how awful my handwriting is – good luck, guys. Finally – you can write numbers down as text. Given execrable cursive handwriting it’s not encrypted, but it’s certainly obscure…particularly if it’s something known only to you (eg. “Julie’s birthday”).
#2 and #3 fail based more on human nature than any technical fillip. Bad guys are looking for quick, easy money, and often aren’t interested in Shannon’s work in order to pick up a few hundred dollars from an ATM (or several). If they have access to a broad range of cards then you have the case of someone who’s paid for (or harvested themselves) a huge number of cards’ data and then spend the time decoding yours instead of doing something faster, bigger and more profitable (like mortgage fraud /s).
These aren’t always the case, of course – criminals work themselves pretty hard for easy money – but if only your accounts are cracked using observation in spite of this method it’s a pretty good (but imperfect) sign that you’re getting special scrutiny.
you could remedy #1 by just using 4 digits that are already written on the card somewhere instead of writing something additionally on it. most card have tons of numbers on them not only your account number but also 24h helpline phone number, card id ,sometimes even manufacturing stuff…
Some people already do this. Or so I hear…
Thanks for this. Actually considering the threats you face and what it’d take for them to be exploited is, imo, what separates actual security consideration from armchair wankery.
If someone is able to get your cypherpins AND all the cards, you have bigger problems. Like the fact that a guy is either following you, or has just mugged you and can get the real pins straight from the horses mouth via the old withdraw-money-or-I-kill-you.
Except the cameras on these compromised ATMs usually point at the number pad in order to get your pin. I haven’t seen one that records the card.
@mmOzct You’re right! They have to have the other card (or a picture of the number on the back) of course, but still.
That’s the problem with one secret / password instead of many. If they can find the one, the whole game is up.
You only need to secure your pin if someone is going to get a hold of your cards anyway. I was imagining a scenario where someone with access to records from a compromised ATM pickpockets your wallet. They have all your physical cards, and they have the two pieces of information required from the video which would allow them to discover your PIN on all the cards.
This is all a pretty low-probability situation anyway. And it’s not that hard to remember your PINs.
Alternative solution, which I think is better that writing stuff on the card, store them on an (offline, password protected) password manager on your phone, if you can’t remember your PIN check your phone before you get to the card reader.
This is the farthest thing from a one time pad you can get! The only important/secure feature of a OTP is that it is used precisely once. Therefore, even if one cipher/plain text pair is cracked the rest remain just as unbreakable as before. With this scheme once one is cracked they are all cracked! Bad cipher, no cookie!
This system is better than nothing, but it is NOT a one time pad and does not provide the level of security associated with such.
This, and every comment like it is partly true. It’s a OTP until it’s reused — so for like the top 90% of the article. You could remember different key material for each card (or as some suggest, use a number already on the card), and then you’ve got a solid OTP.
What I do — and I really do this — is a cheat. As I mentioned in the article, the multi-card PIN method _is_ breaking the rules. But because the PINs are random, it prevents the XORed ciphertext attack from working, which is the case I care about — someone finding my lost wallet and heading off to the bank.
As you mention, it doesn’t work if someone can figure out the single secret. That’s because there’s a single secret. If someone can get it — observing me type, for instance, and correlating it with the number — I’m hosed. If they can then manage to steal my wallet, I’m double-hosed.
But that’s not the situation I’m worried about. People who could steal my wallet after filming me using an ATM could probably also just mug me straight up. Those guys get a free pass at my bank accounts anyway.
That said, I do like the suggestions to use some numbers elsewhere on the card. Very clever, commenteers.
No, it actually is an OTP. The way it is described it is actually a polyalphabetic substitution, or Vigenère cipher. However, because of the way it is implemented it can technically be seen as a repeated encryption of the same four digits over and over again with a bank supplied random key. There is no characteristic of the cipherstream which can be used to gain information on the rest, assuming PIN generation is truly random. It can only be cracked by trying all possible combinations of the first 4 digits.
You are correct in saying that once the first four digits are guessed correctly or otherwise compromised the whole thing is compromised, but from an OTP perspective, that is because the “Plaintext” in this case is trivial, not because of a crypto vulnerability that would result in a crack.
I write hints on the card to remind me. For example, if the first two digits are 72, I might write a reference to something in my life that I remember happened in 1972, like the name of my teacher in 6th grade. If the next two digits are 11, I might use the word “stilts” (two ones look like a pair of stilts).
I don’t have a problem remembering my PINs.
But I do write down four incorrect numbers on all of the cards to mess with any possible thief.
+1
Great Idea, I think I’ll try that.
I wish you’d be allowed/able to designate “tripwire” PINs for such cards.
If someone is attempting a sequential or reverse sequential attack of the PIN, the card account would immediately lock up, and notify the card company. These tripwires could be anywhere above and below the PIN, not just immediately adjacent.
If you’re ever in danger (forced to make a withdrawal at gunpoint, ect.) you can enter your pin backwards. It will work but trigger a silent alarm.
I did not know that!
But I have not bothered using a PIN (or ATM) for about 25 years.
I guess I’d rather take a bullet than let some scum take my money.
I’m pretty sure that is an urban legend. Certainly not going to test it myself…
What if your pin is 1221? :P
http://lmgtfy.com/?s=b&q=snopes+pin+backward+police
…>.<
If the card has the PIN checksum, then you can find the 4-digit PINs that hash to it. You’ll typically get 40 or so possible 4-digit PINs. Run those against standard PIN ranking lists, or target’s address, phone numbers, birth date etc. and you might get lucky.
at 4 digits with only numbers that’s only 10k combination any computer can brutforce that in max a few minutes such a card would be inherently insecure. that’s why as far as i know the hash is never on the card.
Ok, uh… one of the main things wrong with security is all the bad advice out there. Now, this isn’t too bad for a low security method that is unlikely to be broken (generally because nobody would bother), but he’s completely screwed the terminology. What he’s using is a key. A OTP has a completely different meaning… one which he kinda acknowledged when he said maybe you shouldn’t use it more than once. (Duh?)
A OTP is a perfectly random sequence of numbers… imagine a spy using a scratch pad filled with numbers. You use each bit on the page exactly once, one bit for every bit you’re encoding, and scratch them out… never to be used again. Someone else has a copy of your scratch pad’s pages, and they do the reverse (simple XOR works just fine). Nobody is EVER cracking it, unless they get access to the source pads. There’s nothing to crack… literally no sequence of key bits has any relation to any other, and the complete lack of reuse means even solving some of the key (by somehow knowing what was encoded and where it aligned in the data stream) doesn’t help you with any of the rest.
Let me preemptively clarify why fixing bad terminology matters. If someone reads this, and later reads that OTPs are unbreakable, they might quite reasonably confuse the two and think this is awesome security. It’s not… it’s maybe good enough for a normal person who is at low risk of being targeted.
Ok, example time. Say you’re a person with secrets I want to know. I watch you, and see you looking at these numbers written on cards and things, and obviously thinking in your head before entering a PIN. It’s obviously a simple cipher. I break into your house when I have plenty of time to look around… and find your safe with a PIN lock, and a gun box with a physical number spinner lock. Both have 4 digits written on them. I spend a few hours going through all the combinations on your gun box until it opens (it’s not that hard, really). I now know one of your decoded PINs. I spend maybe 30 minutes (max, probably 5) with your decoded pin and the PIN safe before I find the cipher that works and your safe is open. I then conspire to “borrow” your wallet by bumping into you to take it. While borrowed, I write down the numbers on everything there and what they’re for. I’ve now access to all those accounts.
Any combination lock worth a damn will have an exponential back-off time after a few wrong PIN attempts to thwart brute-force attacks.
I’m yet to see a purely mechanical lock (as described for the gun box) with an exponential retry timer in it.
Then it’s not worth a damn.
I’m assuming you already have a high level of confidence in your skills as well as the amount of money you’re going to steal because this seems like an awful lot of work to go through when any self respecting criminal would move on and look for an easier target.
4-digit PINs are still a thing? I have had a 6 digit pin for my bank card for at least 15 to 20 years now… and my credit card has a 6 digit pin too, but i never use that pin anyways, so i completely forgot that number a looong time ago.
+1
Kindly explain this to my bank, will you?
Still standard where I am in the USA.
Still standard in the entire planet you mean.
We don’t even have pins on our Credit cards in the US and everyone is somewhat begrudging that we “have to use the new chip” technology…
I don’t like the chips because they are slower, and because you put your card in and let it go you are more likely to forget it.
I also had a chip fail, it was frustrating, that the swipe could’t at least function as a backup.
I like the idea quite a bit. I’ve often thought of getting or building a hardware password/pin keeper (think mooltipass), but always thought those were too cumbersome and were just another thing to have to carry around.
I have some hope that NFC will wind up being an authentication medium within my lifetime. That’s not to say that we’ll all have *one* NFC identity or anything as silly as that, but that NFC could be used to allow public key based authentication and allow the NFC device to protect the private keys however the owner of it chooses (PIN, Touch ID, whatever).
Android/Apply payment systems basically do that.
Exactly. What’s missing is that Apple has locked the actual NFC functionality up to be ApplePay exclusive. I don’t see why the NFC radio and the combination of TouchID and the Secure Element have to be strongly linked. I don’t see a reason why your phone couldn’t, for example, have a Clipper Card (Bay Area multi-agency transit payment card) app that authenticates with TouchID and then uses the NFC radio to pay your fare. Heck, that functionality on the watch would be unbelievably awesome.
Woe to any that have a rooted phone.
Apple’s secure enclave architecture seems to have done a good job. The touch ID sensor is linked directly to the secure enclave. I posit that just about the only avenue of attack is to trick the user into touch-authing to get them to authorize a fraudulent purchase.
Not to say that such a thing would be *good*, but it’s not nearly as bad as being able to just rifle off purchases or cash transfers in the background without the user knowing.
And the NFC radio itself isn’t part of the trust system at all (you could do ApplePay with megaphones across the parking lot and it would still be secure). That’s what makes Apple’s decision to lock apps out of NFC so puzzling.
Rather than remembering an OTP number which is the same across all cards, why not use a pattern of digits from the card? For example, first four digits, first digit of each group or any other pattern.
That reduces the memory load, and wouldn’t be straightforward to break for another card even if someone sees your written number and observes your PIN.
That is a bad idea because all of the information needed to decode the PIN is on the card it’s self.
But maybe a mod-10 addition of the secret, 4 digits of the card number, and the number you’ve chosen to write on the card.
This adds a tiny amount of extra work to decode the PIN and it makes it like twice as secure; an attacker would need to have access to at least *two* raw PINs and the cards they belong to in order to figure out the encoding scheme.
Um. I don’t care if the data you’re encrypting is random, if you use the same key for multiple data, it’s NOT a one time pad. By definition.
I have used a similar but likely less-secure method of obfuscation for my PINs, but I made one small change that I think might help and is applicable to any such scheme. If the encrypted PIN is a permutation of the original, I slightly alter it in a simple way that is easy to remember. For example, if my PIN is 3578 and it encrypted to 5837, I’d write down 58381, with the final 1 reminding me to subtract 1 from the previous digit before decrypting. My theory is that if anyone got their hands on my encrypted PIN, they might try all permutations of those digits first, so the encrypted number shouldn’t be a permutation of the original.
Speaking of One Time Pads (even if it is used wrongly in this case).
The HackADay Store still lists a OTP for sale.
https://store.hackaday.com/products/1407981609
I don’t know if it’s just me, but I really don’t have a problem memorising random numbers like this. I’ll have it on a peice of paper for maybe a week, and then it’s in my head.
I still recall my exam numbers from 2001 or so. Also friends phone numbers, and such like that.
d6nw5v1x2pc7st9m.
Wow, I can remember an ex-employees wifi key too, much useful ;)
Memory is strange. I can remember my childhood phone numbers, but not ones I’ve had more recently. And my ability to retain numbers has definitely declined with age (I’m over 50). And it’s not just numbers. I’ve been singing choral music my whole life and I can recall my part in pieces I haven’t sung since college. But pieces I’ve learned more recently tend to fade. I’ve wondered if this isn’t simply that when younger, my brain wasn’t as full and thus each new memory was a greater percentage of the whole. Or maybe my brain finally figured out that keeping the tenor part to some random song in my memory wasn’t really worth it.
No, it means you are toast.
Use a set of phrases that mean something to you. I use this one (not really, but you get the idea). For PIN 3161323: See as far as can be seen. C =3, a = 1, F = 6, 1 3 2 3. Mirror the numbers if you want to get more clever. It’s in your head, so nobody can decipher it. Change it up to a different phrase if needed later on (PIN change requirement). make the phrase memorable that suits the venue. Use a foreign language. Sport metaphors. Whatever works for you. I have not forgotten any important numbers in decades.
.
Yeah, ok, good discussion, good solutions, but since you guys seem to aim for something unbreakable, I’m afraid you all fail. As a criminal, I’d just tie you to a chair, shoot one of your knee caps, and then point the gun at your balls. And hey presto, I broke the security you spent weeks devising.
If you are that concerned that the guy/gal that nicks your card also has a PhD in cryptography and is determined to steal from your bank account when he/she could just switch to one of the other low hanging 100 nicked cards, can I suggest living in a cave and paying your goods in bear skins?
None of my passwords are particularly hard to break, yet I got hacked only once, and that was my Yahoo account. Ahah, I hear you, serves you right for not having long complex passwords easy to break! They didn’t, they just hacked into the server and leaked the users database, remember? The guy with a 64 random characters password got hacked just as easily as me, except it’s always been easier for me to log in.
Also, at least I don’t have a Farcebook/Linkedin/etc account where I spill the beans about security questions such as my mum’s maiden name or my first school. Because if you do, then it doesn’t matter how far fetched your password is: whether your password is 1234 or GF6@57?H$kjg, you’re prone to password reset all the same.
If a guy holds a gun to your balls, you’d give him the pin wether it’s encrypted or not. so… it’s not really a valid argument.
So the take away here is to let only women remember your passwords? If the subject doesn’t have balls, your method fails.
This is almost exactly what I do.
I have my “Magic Number”. (the street address of a girl I use to date)
Then add it to the expiration date on the card, and boom, there’s my PIN.
If it goes over 9999, I just use the last four digits.
In the case of no expiration date, I use the last four digits of the card number.
Every few years, we get new cards, and then it’s time to change my PIN.
So far, no two cards have had the same PIN.
“HOW A HACKER REMEMBERS A PIN”
Hackers don’t simply remember a PIN, they hack it.
Lifehacker is more accurat
I had a job where we needed several locks for our kit. One colleague used combination locks and engraved his encoded combination on them all. It made a real impression on me. He wasn’t a hacker.
I’m considering putting tape over my card’s numbers, because with the new chip crap anyone nearby can see the top of the card for over ten seconds.
Real secure. :/
That chip crap makes (or will eventually make) the fact that they can see the numbers on the front moot.
Unless you purchase online, or under $5 at the register.
I boldly predict that online purchases will eventually wind up having strong authentication one way or another. And Europeans have been doing small value “offline auth” purchases for a long time now with chips.
In Australia, the limit is $100. Wave the card over the reader, it beeps, and the goods are yours. Absolutely NO QUESTIONS asked by anyone! Get some groceries, fill up your car, buy some shoes… one can ratchet up over a grand before most people even realise their wallet is missing!
And consumers in Australia are lapping it up!
A small drill bit through the card in the right spot to sever the antenna coil works well.
Heh heh, one tiny smack with the hammer and I disabled the “tap” capability. Stupid chips in everything; RFID isn’t secure.
$100, Wow! I’m truly surprised at that.
My old wallet did it for me. Where the cards stuck out of the top of the slots a small crack would form in time and break the coils.
You can think of the one time pad as reducing the sample size to one adbots method of obliterating statistically significant relationships between plaintext and cyphertext. This works, bit it is a corner case that is of limited practicality (although PINs are a situation in which it may actually be useful).
I just use a mnemonic device. For each digit I choose a word that has the same first 1-2 letters and then I use them as a sentence that ends up stuck in my memory. For example 6689 can be encoded as “sitting still eating nuns” in English. My native tongue, Polish, is more flexible when it comes to grammatical structure…
There is an urban legend here about some man who used ATM outside his bank. One day he came in and started screaming at poor clerk. Finally a manager intervened and asked, what seems to be the problem. It turned out that guy had written PIN on the wall of the building, and few days earlier bank repainted it…
I wrote down all my master passwords in a “word find puzzle* with 10 actual words and a description to find 10 fruit names. Obfuscation is highly underrated. I also use certain chess move sets with my keyboard as the board to visual remember it. Very easy for me, but to a pc a keyboard layout is arbitrary.
I’m using this approach in my password manager. I call it “sweating”, since it’s basically a salt that is provided and stored by a human.
Well now I will have to change the way I do it. I have been using this exact method for the last 10 years or do…
About 15 years ago I made all the PINs for all my cards the same. One number to remember, never been a problem. If it gets compromised I’ll just get new cards and change them all to a different number. Why make things complicated? The number one way of PINs being stolen is rigged ATMs, at that point it makes no difference how amazing your PIN choosing system is.
‘Suppose the PIN is 1234 — it has to happen so someone, right?’
It happened to me, in 1993.
A decade ago my security code on the back of one of my bank cards was 123.
That’s amazing. I have the same combination on my luggage!
My bank can issue (for a small fee) a small battery powered card reader that you can use to set up a one-time PIN so I virtually never use the same PIN twice. Good luck ATM hackers!
If you’re going to write the pin on the back of your card, at least write it backwards.
Most atms are programmed to act normally but when it dispenses the money, it only comes out half way and locks down on it. Meanwhile it automatically alerts the athorities and records full video instead of time lapse.
This way if someone takes your card and tries to use it at an ATM, they would be caught on camera.
I have tried typing my PIN backwards and just got the ‘Wrong PIN’ message. Also I know people whose PINs are palindromes, such as 1661. So this won’t work everywhere.
My grandmother had it written down in a special code in the address book. Say that the bank pin is 1234 then in the address book she had (among all other addresses)
Jane at the bank:555-1000 x1234
555 eh, sure that’ll fool everybody.
And interestingly most women hide their pincodes in inconspicuous looking text I noticed. So I guess the criminals of this world are probably aware of that too. Although the pickpockets and robbers probably won’t bother going clever and will not go through the effort to look for it.
Also most all cases of stolen cards is skimming and watching/capturing you entering the number, making hiding it or coding it on your person rather pointless I would say.
The phone number she used was a real bank phone number
I agree with your view on skimming attacks. I would suppose pickpockets will go for the low hanging fruit like anybody trying to make a buck; why glean through wallet contents when their time would likely be better spent moving on to the next wallet. FYI/reminiscing: In the 1990’s in Vancouver, BC I recall offshore businessmen being referred to as armoured cars because of the large amounts of cash they carried.
I think this proposed security method is most effective against the people in your life. Most instances of card theft/fraud among people I know has been from people they know(and all substance abusers as it happens). If there is a junkie in your life (and you may not know it) this will help.
If this method is used by 100 people chances are 75 of them will use the secret code 1234…
That’s how people are. And THAT is the flaw. And is actually using statistics as a hack I might add.
Sadly, that is most likely true. 1234 or 1111 or the expiration date or their birthdate. Tell them to use better passwords and get told that you’re a ‘tinfoill hatter’…
Well, maybe so, but I doubt I’ll have to ask the bank to lock my accounts anytime soon.
As for mathematicians it will be 3141. Elec eng : 1414. Physicists … 6022, etc etc.
A couple of decades ago my secret number was 1684 form the old Pic16c84.
… and a “hacker” 6502?
Except that because you’re using modulo addition, encrypting the pin with the secret is mathematically the same as encrypting the secret with the pin. And you’re using the same secret for each card, so it’s really not a one-time pad at all and as soon as anyone gets a PIN for any card they have your secret.
I just add the end numbers of my CVV number on the reverse of my card and use the unit if >10 and add that to my CVV number eg 456 becomes 4561 as my PIN. Not foolproof but no one would naturally guess it. Never need to memorise a PIN anymore. Do it this way for over a decade ????
I’m surprised BCD and XOR don’t get a mention here… encode the “pin” as BCD… then XOR it with a secret 16-bit key. Not difficult to do in your head either.
You can obfuscate before encryption, using a second number and just adding our subtraction before applying the one time pad. Much like using dual ciphers, you increase the n-space difficulty by instead of writing the encrypted pin on the card, write the encrypted operand instead making the length dissimilar to your pin.
You can also use a smart pass generator – so that you do not need to remember your passwords. Just use it the smart way. What it does is encrypting one pass you remember into many pass for many systems/users. It’s simmilar to pass manager, the difference is – your passwords are not stored anywhere permanently. Got it ? :)
In that scenario, it’s extremely weak.
1. You try to use your first card, they see the 4 digits on the back
2. They refuse the transaction. 99% of the time, you’ll use another card with another 4 digits on the back since you are a *honest* guy starting to feel disturbed about a bad bank credit and you want to prove you are solvable.
3. We mod both number: presto they have your secret code, and all your PIN.