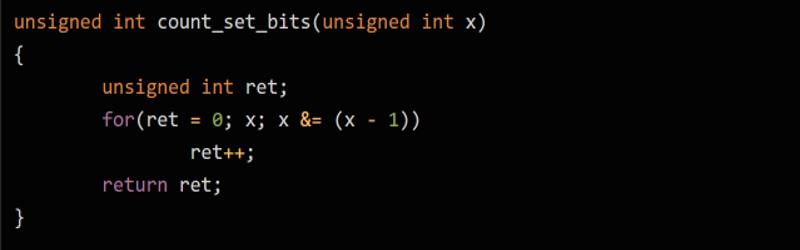
If you like nitpicking around C code and generated assembly language — and we’ll admit that we do — you shouldn’t miss [Scaramanga’s] analysis of what’s known as Kernighan’s trick. If you haven’t heard of the trick, it’s a pretty efficient way of counting bits.
Like the Wheatstone bridge and a lot of other things, the Kernighan trick is misnamed. Brian Kernighan made it famous, but it was actually first published in 1960 and again in 1964 before he wrote about it in 1988. The naive way to count bits would be to scan through each bit position noting how many one bits you encounter, but the problem is, that takes a loop for each bit. A 64-bit word, then, takes 64 loops no matter what it contains. You can do slightly better by removing each bit you find and stopping when the word goes to zero, but that still could take 64 cycles if the last bit you test is set.
Using the trick, you make the observation that X & (X-1) will always clear the least significant bit of a word. Try a few examples:
X X-1 X&(X-1) 0001 0000 0000 0010 0001 0000 0011 0010 0010 1010 1001 1000 1100 1011 1000 1111 1110 1110
You can probably see where this is going. By computing X&(X-1) you clear a bit on each loop iteration and you only have to go through the number of bits that are actually set.
This kind of thing is a common enough type of interview question although as [Scaramanga] points out, compilers will probably optimize this to use specific CPU operations and get even better performance. The POPCNT instruction on the x86 architecture, for example, will do it all in one instruction. He also has a detailed explanation of exactly why this works the way it does.
Of course, most software doesn’t need to run so fast that it is worth using obscure tricks. But sometimes it makes sense. It is also a nice test of logic and problem solving in an interview situation.
If you like this sort of thing, be sure to check out [Sean Anderson’s] extensive list of bit hacks. It shows several different ways to count bits and do other common and uncommon tasks with different tradeoffs. For example, you could dedicate a 256-entry lookup table and do the whole thing with one loop per byte with great speed but bad memory utilization. Always a trade-off.
There are lots of ways to play with bits, especially in C. Or you can use tools to chop things up if you just want to analyze them.















“The POPCNT instruction on the x86 architecture, for example, will do it all in one instruction.”
Obliterating the need for the “trick”.
“Of course, most software doesn’t need to run so fast that it is worth using obscure tricks. But sometimes it makes sense. It is also a nice test of logic and problem solving in an interview situation.”
Playing a game of Exapunks such tricks might come in handy.
You could pre-compute the bit counts for 0-255 and store it in an array. So look up the bit count of number n by using it as an index to the array containing the bit count. If you need to handle larger word size, just add up the count of each byte sequentially.
It should be pretty fast compared to a loop and the 256 entries array doesn’t take much space.
Only if you can keep the whole table in L1 because the first cache miss will be slower than the whole Kernighan iterative process.
Be careful: optimising for number of instructions executed is NOT the same as optimising for speed.
A list of 256 values, each one byte large would only need 256B of space in L1.
Most modern CPUs have tens of KB of L1, so a 256 byte trade for on average of about 4 times the speed compared to the Kernighan trick might be worthwhile.
Though, one could run into other bottlenecks along the way.
But how does one insure that the table STAYS in L1? Wheather there is sufficient space is not the relevant question…
That is truly the more important question.
If one could lock things into L1, then that would be one solution to the problem.
Some processors have scratchpad memory that also could be used to lock data very close to the core, but if that applies to L1 is a different question and varies from architecture to architecture. (some architectures doesn’t have scratchpad memory to begin with….)
Though, at the very same time, one will access those 256 bytes like a maniac while doing the bit counting, so the caching system should not have too hard of a time figuring out that it might be good to have around.
Popcnt instruction on x86 can do 4 bytes per clock cycle. No lookup table can beat that. L1 is 4 cycles away, plus you need to do an add to get the location in the table first.
Arm has a similar instruction as part of NEON. RiscV has one too. Some DSP processors also have dedicated bit counting instructions
There are lots of microcontrollers that doesn’t have L1 that would get the benefit of trading a table lookup over a tight loop. Microcontrollers out number processors.
Note: Ostracus mentioned that POPCNT or similar instructions would eliminate the need for the algorithm for the x86 or other more advanced processors.
Even if the memory access causes a cache miss in a more *advanced processor* on the first access, chances are that the other execution units (even in the same core) could be doing something else that are not dependent on the result.
Also subsequent lookup for a word or long word would be in the cache.
I benchmarked four different algorithms.
First place for 32 bit integers with a small margin is this one. The builtin single instruction is second and trades places for first place with the 64-bit version.
Pretty fast, and and beats the “promoted” algorithm by a big margin is:
x = (x & 0xaaaaaaaa) >> 1 + (x & 0x55555555);
x = (x & 0xccccccccc) >> 2 + (x & 0x33333333);
x = (x & 0xf0f0f0f0f0) >> 4 + (x & 0x0f0f0f0f);
x = (x & 0xff00ff00) >> 8 + (x & 0x00ff00ff);
x = (x & 0xffff0000) >> 16 + (x & 0x0000ffff);
return x
In the first line we use the 32-bit word to hold 16 two-bit variables at once. Each holds the number of ones in the original word in the same two bit positions. Then we use the 32-bit word to hold 8 4-bit(only 3 bits used) variables. And so on.
“this one” in the first line of my comment is the one this comment replies to: table of 256 entries.
Yes, old school “hacking”. And only a few instructions on many CPU’s, like ARM which has barrel shifting in all instructions. Lots more in Henry Warren, Jr’s book, which is rather dry unless you really like this!
I think this is more useful for testing if a positive number is a power of two or not.
I came up with this on the spot in a CS interview 3 months out of undergrad. I’m always annoyed when obvious things get some random dude’s name attached to them like they did something special.
This is the difference between x science and x engineering. In computer science you learn each clever algorithm by name and memorize it, in computer engineering you are taught the tools and figure everything out on your own. Different learning styles that have different merits
Did you prove it was true for all cases?
“some random dude”!?!?!?!?!?
Turn that music down and get off’n my damn lawn!! >:-(
standing on the shoulders of giants and not even knowing them as more than random dudes, quite sad.
So co-writing C and Unix isn’t special, but you knowing of C somehow is special?
Sounds like you might owe “random dude” for your first job out of undergrad :P
Except, our “random dude” did make a statement in regards to their involvement in the creation of C, saying simple “it’s entirely Dennis Ritchie’s work” – Brian Kernighan
Coding is not a job that requires rote memorization like some tax law accountant. Leave that to historians or sport trivial that one needs to remember the names of players or their scores.
Funny that they expect you to solve a famous problem/proof in an interview or an exam with only 10 minutes when the original person who have more training might have spent a few weeks/months/years solving.
Thankfully what they are after is not the name of the person that solves it but rather the *thinking/problem solving process*.
+1 – I suppose everyone has heard of Newtonian Physics
If only someone wrote a benchmark to test what compilers do with bitcounting….
bitarrays.cpp
https://gitlab.com/chriscox/CppPerformanceBenchmarks
Don’t forget doing multiple additions or comparisongs with a single addition operation: https://devblogs.microsoft.com/oldnewthing/20190301-00/?p=101076
I recommend the book Hacker’s Delight. https://www.hackersdelight.org/
I found the trick sentence is slightly confusing, after working though it I think the word **set** is missing.
“Using the trick, you make the observation that X & (X-1) will always clear the least significant **set** bit of a word.”
The confusion related to the least significant bit is always bit 0, where as the least significant **set** bit may not be bit 0.
Thank you!
Beware that the time the algorithm takes to run will be dependent on the data. That can cause a side channel data leak.
hmm… as a non native english speaking person, I always thought that “least significant bit” reffered to the bit with “position” 0. But the text seem to imply that “least significant bit” means the bit with the “lowest position” that is set (is a 1). Do i understand that correctly?
“Least significant bit” indeed does refer to the bit at “position 0”. A more clear way to have phrased it in the article would have been “least significant set bit” or “least significant non-zero bit”.
Would it have killed the writer to explain what the “&” operator does?
No, but in the context of the article it is assumed to be the “AND” operator. When writing, the author will usually have a target audience in mind and assume some things to be understood.
You can learn about operators here:
https://en.wikipedia.org/wiki/Operators_in_C_and_C%2B%2B
Further, the truth table for AND is a follows:
1 AND 1 = 1
1 AND 0 = 0
0 AND 1 = 0
0 AND 0 = 0
If this piques your interest you can venture into sentential logic – which is highly extrapolated, but always holds true in programming language (regardless of the symbols), and in real life.
Have fun :)
https://en.wikipedia.org/wiki/Truth_table
Col. Jessup: “You can’t handle the truth”-table.
https://en.wikipedia.org/wiki/Propositional_calculus
Furthermore, since I haven’t seen an XKCD in the comments recently:
https://xkcd.com/704/
If you study enough you’ll eventually see the humor.
Groovy, so, say there are 8 switches on an 8-bit port, and we are looking to see which active switch has the highest priority… wire them such that the highest-priority is at bit 0, lowest at bit 7. Now, locating the highest-priority active bit is accomplished in the same number of executed-instructions, regardless of position.
(X-(X&(X-1)))… may be useful in e.g. interrupt-processing, where cycle-counts matter.
“Kernighan’s method”? The method was proposed by Wegner P. in 1960 paper “A technique for counting ones in a binary computer”. As stated in [1] “The downside of the Wegner approach for modern processors is that the unpredictable loop termination adds a mispredicted branch penalty of at least 10 cycles, which for short loops can be more expensive than the operations performed by the loop.”
A useful comparison of known pop count methods can also be found in [2]
[1] https://arxiv.org/pdf/1611.07612.pdf
[2] https://homes.cs.washington.edu/~cdel/papers/spost106s1-paper.pdf
What they miss are the great engineers who freeze doing time-pressure interview quizzes.
I’m really surprised nobody mentioned this, but POPCOUNT is commonly known as the “canonical NSA instruction”. It is rumored that in the 80s, the NSA told Cray it wouldn’t purchase a supercomputer which didn’t do POPCOUNT. When I worked at SGI, which owned Cray, I head this internally on multiple occasions.
So assuming this is true, why? Why is this so
It’s noted that lots of old military ciphers where LFSR based, and doing an AND to mask the taps and a POPCOUNT to determine the number of 1 bits in the result would be an efficient way to implement it the feedback. I’ve been told by people from various 5EYES agencies that 70s ciphers often had 24 or even 32 bit keysizes, so it could be they were simply brute forcing and this would have significantly sped up an implementation.
The other is to measure hamming distance.
If anyone has a better idea, or anything beyond hearsay, I’d love to know.