When it comes to architectural features, there are probably not many as quintessentially memorable as arches. From the simplicity of the curved structure to the seemingly impossible task of a supposedly collapsable shape supporting so much weight in mid-air, they’ve naturally fascinated architects for generations.
For civil engineers, learning to calculate the forces acting on an arch, the material strength and properties, and the weight distribution across several arches may be familiar, but for anyone with only a basic physics and CAD background, it’s easy to take arches for granted. After all, they grace the Roman aqueducts, the Great Wall of China, and are even present in nature at Arches National Park. We see them in cathedrals, mosques, gateways, and even memorialized in the case of the St. Louis Gateway Arch. Even the circular construction of watch towers and wells, as well as our own rib cages, are due to the properties of arches.
But what really goes into constructing a strong arch?
Basic Concepts
Arches share many key concepts with chains. For one, the weight of the arch does not contribute to its shape, but the distance between its ends does. Every shape formed within an arch of a certain length (measured by its circumference) is known as a catenary, with similarities to parabola.
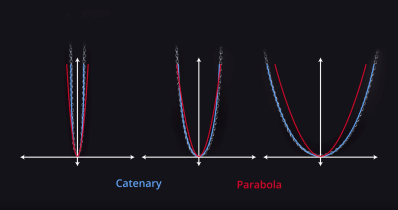
While arches do end up being durable and long-lasting structures, when they are not shaped appropriately for the loads they are meant to carry, they can collapse. Given the similarities between arches and chains, the angles needed to carry loads in the chain (a tension system) can be mirrored in the angles needed for an arch to carry the same loads.

The Basilica of the Sagrada Familia in Barcelona uses the same techniques for its magnificent arches. Architect Antoni Gaudí initially built an upside-down model of the basilica, adding weights proportional to the roofs and other features he intended on adding to the structure. The resulting profile was the exact shape necessary for his arches to support the weight of the rest of the basilica.
For bridges, since there are not heavy static forces, so long as the arch has sufficient weight of its own, it does not need to take into account the position of its loads. This is due to the fact that similar to adding weights to a heavy or light chain, the heavier the arch, the less it transforms from the application of loads.
Modifying Arches
One interesting quandary for most people is figuring out which arches are able to support their own weight. University of Waterloo professor Wayne Brodland explains in his course on engineering models that as long as an arch is a mirror image of a chain of the same length hung from the same end points, then its shape is valid and can stand under its own weight.
This accounts for heavier semicircular arches, lighter arches with wider endpoints, and taller arches with closer endpoints and is known as the chain test. The test requires that a chain be able to fit within the arch when it is mirrored upside down. This also explains why thicker arches are able to adopt shapes that thinner arches cannot.
Another option is to adapt the shape of the chain to the shape of the arch. Since this requires outward forcing pulling on the chain, reversing these forces to push inwards on the arch allows it to hold up its shape.

Arch Supports
Rather than simply modifying the end points, however, the horizontal forces can also be provided by the stuff that surrounds the arch. Often, this takes the form of bricks and concrete around bridge.

In the case of the Hoover Dam, the shape of the structure holding back the water in the dam is shaped as an arch on its side, with the load against the top of the arch. In this example, it’s clear that the shape of the arch can be mirrored in the shape of a chain.

[Thanks to Chris Lam for the tip!]














A pedantic point: The upside down chain model by Gaudi shown in the article was for https://en.wikipedia.org/wiki/Col%C3%B2nia_G%C3%BCell not Sagrada Familia.
the shape of the hoover dam is an arch. It is not a catenary. The hydrostatic pressure is uniform for a given depth (plan section) and is normal to the surface of the dam. The catenary (from latin: catenaria, “chain”) is assumed when the external force at each point of the structure (such as that provided by gravity) is in the same direction. This generally means that at only one point in the section will it be normal to the section. The dam structure in this case is an arched gravity dam, so both the sheer mass of the structure and the load transfer to the walls of the canyon are important. In a pure arched dam of negligible thickness and insignificant height, the shape of a plan section would be a segment of a circle.
One of the major contributions of Brunel was proving analytically that a semi elliptical arch can also work.
https://en.m.wikipedia.org/wiki/Maidenhead_Railway_Bridge
http://www.engineering-timelines.com/scripts/engineeringItem.asp?id=441
No mention of the DaVinci bridge, which made Popular Mechanics last week:
https://www.popularmechanics.com/technology/infrastructure/a29426711/da-vinci-bridge/
“While not all arches are built from bricks, all arches do exhibit tension between points of contact of their construction material, forming a compression system of connectors pushing against each other. This works to a builder’s advantage, as the friction between materials coupled with this tension allows the materials to stay in place.” – you mean “do exhibit compression” and “coupled with this compression” right?
An arch is not a specific shape; it is a structure spanning some distance, that carries the vertical loads primarily as internal compression due to its shape and the way it is supported. That is all. The shape may be catenary, half-circle, semi-elliptical, korbbogen, you name it, but these are all arches. Some of these are optimal (compression only) for a certain kind of loading: catenary for pure vertical loads, circular for hydrostatic pressures and so on. You can build a really slender structure if the main component of your load corresponds the chosen shape. That is why steel arch bridges are often chosen in the 100-300 meter span range.
However, if the load deviates from the optimal – say only half side of the arch is loaded – the performance of the structure is abysmal, as the external loads can only be balanced by internal bending action, for that a slander structure is not well suited.
https://www.youtube.com/watch?v=JlL6ZHChhQE
Just think of how much better McDonald’s is going with arches.
What’s odd is nobody in the western hemisphere developed the arch, or concrete. For unknown reasons the only ancient examples of wheels that have been found on this side of the planet were on some children’s pull toys. Llama on wheels!
It’s not that nobody had the stone working skills to make an arch work, there are plenty of examples of very finely fitted stonework in Mexico and farther south. It’s simply that nobody thought of the concept, so openings in stone walls were limited in width to the longest rock they could carve into a block, without it breaking under the weight of the wall above.
There are several reasons. One major one is that agriculture was practiced on terraced or stepped land in the jungle and hills, which meant that things like wheelbarrows weren’t of much help because you had to get them up and down and across streams and ravines – carrying stuff on your back was easier.
The invention of the wheel for transportation purposes occurred around the fertile crescent area because you had a big oasis surrounded by deserts – trade happened over long distances along relatively flat areas where you could ride chariots and pull carts. In the Americas, the Aztecs, Olmeks etc. used runners over mountain paths and built their cities on artificial islands to gain better access to the waterways.
Another thing for the Aztecs in particular is that they built their stoneworks around areas prone to sinkholes and earthquakes – the ground was soft, so when they built something they just piled a ton of stones and rubble as a foundation until it stops sinking. When they built new temples and monuments, they built them on top of the old ones with proven foundations. The buildings are pyramidal in structure because the ground won’t support lateral forces – trying to construct a large arc would result in the arc splitting as the soil moves around it.
They probably knew how to make an arc, but found no use for it.
And the important pre-requisite for pulling loads with a wheeled cart: tame draft animals. The same difference actually happened in Africa, which also didn’t develop the wheel until much later.
Middle east had horses, oxen, cows… basically large domesticated animals that were tame enough and strong enough to be harnessed for pulling carts.
> They probably knew how to make an arc, but found no use for it.
Yeah probably. They probably knew how to master nuclear fusion as well, too bad they had no use for it.
We know the Moebius strip – why aren’t there any buildings shaped like that? Will historians say we didn’t know it because we didn’t build any structures with the shape?
You only use it if it gives you some advantage.
How is the arch not an advantage? Quansent hut tech was used in missile bases and tunnel etc.