The human mind is a path-planning wizard. Think back to pre-lockdown days when we all ran multiple errands back to back across town. There was always a mental dance in the back of your head to make sense of how you planned the day. It might go something like “first to the bank, then to drop off the dry-cleaning. Since the post office is on the way to the grocery store, I’ll pop by and send that box that’s been sitting in the trunk for a week.”
This sort of mental gymnastics doesn’t come naturally to machines — it’s actually a famous problem in computer science known as the traveling salesman problem. While it is classified in the industry as an NP-hard problem in combinatorial optimization, a more succinct and understandable definition would be: given a list of destinations, what’s the best round-trip route that visits every location?
This summer brought news that the 44-year old record for solving the problem has been broken. Let’s take a look at why this is a hard problem, and how the research team from the University of Washington took a different approach to achieve the speed up.
The Science of Getting From Here to There
The traveling salesman problem (or TSP for short) has been one of the most studied problems in computer science. It was first considered all the way back in the 1800s by mathematicians W.R Hamilton and Thomas Kirkman. Despite what you might think, it actually has applications outside the GPS navigation system on your smartphone. What can be modeled as a TSP includes everything from the layout of ASICs, the school bus route plans, the order of drilling holes for PCBs, to DNA sequencing. The “distance” between points could mean physical distance or similarity between genes.
 In the 1930s, Karl Menger an Austrian-born mathematician who was a visting professor at Harvard and Rice at about the same time, considered the brute force solution that simply considers every possible route. That’s approach becomes dauntingly difficult quickly as just 15 different locations yield 1,307,674,368,000 different routes to compute (that’s 15 factorial). As you can imagine, scaling to hundreds or thousands of different destinations quickly becomes uncomputable. Right around 60 different destinations yields around the same number of possible routes as the number of estimated particles in the universe. And so a classic computing challenge was born.
In the 1930s, Karl Menger an Austrian-born mathematician who was a visting professor at Harvard and Rice at about the same time, considered the brute force solution that simply considers every possible route. That’s approach becomes dauntingly difficult quickly as just 15 different locations yield 1,307,674,368,000 different routes to compute (that’s 15 factorial). As you can imagine, scaling to hundreds or thousands of different destinations quickly becomes uncomputable. Right around 60 different destinations yields around the same number of possible routes as the number of estimated particles in the universe. And so a classic computing challenge was born.
There are several different versions of the TSP such as metric, euclidean, asymmetric, and more domain-specific constraints such as adding a cost to traveling different routes in addition to the distances themselves. This leads to a distinction between the generic and non-generic TSP.
Our Unique Talents
Strangely enough, humans are actually quite good at solving the euclidean version of the problem. Humans can arrive at a near-perfect solution in close to linear time even in cases with more than 120 destinations. The ease at which we can accomplish this feat has fascinated several cognitive psychologists and prompted dozens of studies and papers on the subject. In fact, this same ability has been shown in pigeons and shape-shifting bacteria.
The current hypothesis is that humans have several heuristics or shortcuts that make them very good at satisficing — a term coined by Herbert A. Simon that simply means arriving at a decision that is “good enough”. Most of what computers do is calculating a specific and verifiable answer. It is correct or incorrect with no room in between. It is much easier to arrive at the perfection solution than it is to define what is good enough given the current context.
The Approximate Solutions
In this vein, computer scientists over the past half-century have been refining and applying new techniques and approximations that computers can use to sort of guess their way to a better solution. Techniques such as dynamic programming were able to get the number of routes to calculate down to n22n or 7,372,800 possible routes for 15 destinations, a far cry less than one trillion. Branch and bound algorithms are able to get that even lower but so far, it hasn’t been proven that there exists a perfect algorithm that evaluates less than 2n routes.
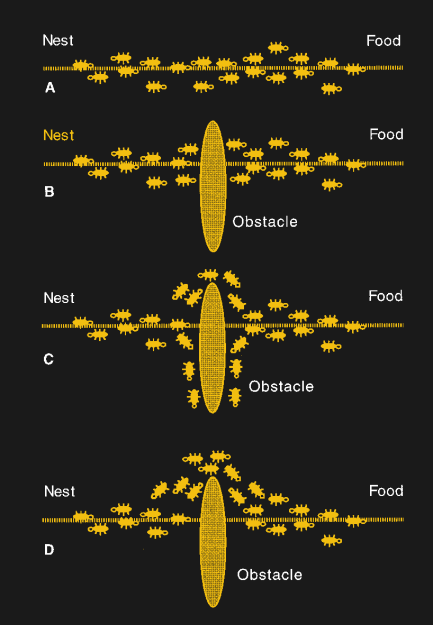
This is still largely unreasonable for larger data sets and so approximate solutions needed to be solved for rather than perfect ones. Heuristics such as Nearest Neighbor, which simply goes to the nearest destination that hasn’t been visited, randomized searching using Markov chains, and even simulating ant colonies are all solutions that are used to produce approximate solutions. However, even the best of these algorithms are only able to guarantee that their solution will be at most 50% longer than the perfect solution.
A Razor Thin Improvement is Worth More than Face Value
While we’ve seen hardware being thrown at the TSP in both custom accelerators as well as the sheer number of cores working on the problem, there haven’t been any algorithms able to break that 50% number. Until the recent preprint paper published by Anna Karlin, Nathan Klein, and Shayan Gharan about a new technique that offers a slight improvement for the metric version of the TSP. The improvement just shaves 10-34 off that 50% number. That may not seem very much and you can argue that it is so tiny that it doesn’t matter on all but the largest data sets.
However, the key is that it was mathematically demonstrated that improvement was and is possible. The record of the past 44 years has been broken and the authors of the paper hope that it will inspire others. A similar breakthrough happened in 2011 when the graphical case of the TSP saw a small improvement. That small refinement inspired other researchers who developed redesigned algorithms. What started as a simple augmentation eventually lead to breaking the barrier of 50% all the way down to 40% for the graphical case.
The takeaway here is that problems can be solved. Even problems that seem like you’ve hit a limit that can’t be solved. It’s nice to find that 44-year-old problems still get some attention, pulling the state of the art along with them as new eyes find unexpected approaches.
















Heck, I’m still waiting for the general feedforward solution to the 3-body problem. In my case, I don’t care where Jupiter will be in 100 years to within a foot.
But I care greatly about being able to efficiently model the behavior of individual molecules in a fluid.
More specifically, the ions in a plasma with such and such a field and gradient applied.
The existing math doesn’t get you there (similar set of problems) and here, we have “gravity” with both polarities and different values of g (charge/mass ratio).
Accelerating plasma more or less coherently (laminar-like flow) would give us electrostatically driven fusion with gain, just to toss out some goal-orientation. It’s kind of my hobby. By not wasting energy putting it into spurious degrees of freedom (like just heating things up and hoping some collisions are head on) – you do far better – other losses are also far lower.
And yes, I’ve talked to the vendors who make various kinds of physics simulation software (it’s not cheap but…), and they’ve all basically said “keep your money” – it’s a “heat death of the universe” class problem to do it by the usual perturbation and math errors would kill you anyway during iterating – just like with telling me where Jupiter is going to be by the same methods.
Cut and try experiments show there’s possibilities, but the number of things to try – even with the best simulator – reality itself at least runs in real time and it’s really accurate – is so high it’s ridiculous. Takes awhile to build each setup.
Math used to be the queen of sciences. It’s not so much anymore. It’s not that it’s broken, exactly – if you give me a material and I know some things about the molecules it’s made of (and any internal structure for meta materials) I can use existing math to tell you pretty much everything interesting about that material.
But there is NOTHING that lets me put in “I need these properties within some tolerance ranges” and have it tell me “here’s how to make that out of what there is on the periodic table” – for just one example – we have feedback but no feedforward for a whole lot of existing science math.
But it’s been mathematically proven that the n-body problem for n>=3 doesn’t admit a analytical solution, while the TSP is an NP-hard problem for which we’re still not sure if a P-time solution exists (which depends on P=NP, which is most likely not true).
Of course the obvious reply must include something to the effect that eventually computational resources will catch up to the problem. I vaguely understand the concept of quantum computers so perhaps that will be an applicable resource toward solving this “puzzle” (in only 64KB of memory).
Traveling Salesman Problem has been been studied to death many times over. I remember my professor giving a PCB manufacturing example of this to minimize the CNC travel distance between drilling holes for components. Thinking back on that, formulating the problems still remains the domain of people. Also, don’t forget that with creativity you can turn the problem upside down and come with a solution that eliminates the problem altogether like switching from through hole to surface mount components.
Speaking of magpies,
don’t corvids have really good brains for solving such problems as TSP?
In a previous life I was a fedex courier, and the traveling salesman problem was solved thrice daily (before 10:30, the rest of the delivieries, pickups) and had to include things like bonus efficiencies for normal flows of traffic, extra time allowing for bridge lifts, extra stops, semi-permeable barriers, and time for customer connections at each stop. Also, distance mattered less than time.
Perhaps what makes this impossible for computers and a piece of cake for humans is the context we bring to it. So many things outside of the problem inform the solution, and then when we are asked to perform the traveling salesman problem itself, we engage the art and fluid dynamics side of the thing instead of pure distance calculations, but then restrict our formulas to the least useful dataset.
It is inspirational to make progress on the TSP. Perhaps there is some inspired thinker who can reliably knock off more than a whole percent based on the application of solutions from another discipline. Go math!
[B2]
You sank my Battleship!
In that case you will know that it pays to plan the route so that you have to take the least number of left turns…
The reason is remarkably simple: We drive on the right side of the road, so taking a right turn you onbly have to get one space to enter trafic from the left, while turning left you need to have room on both lanes, which costs more time…
I have a recollection of a problem similar to the TSP that I had to solve in the
begining of my professional career that was the following:
Given a list of targets in the sky (stars) which you had to observe one by one
during the night; what would be the best order of the observations to guarantee
that each one was observed the closest possible to meridian crossing (to minimize
atmospheric refraction effects). The targets were spread along the whole celestial
sphere. Remember, the targets move with respect to the meridian along the night,
as Earth rotates, and you have to spend a period of time (tens of minutes)
observing each target.
I solved it with the same approach somebody mentioned for the PCB routing problem:
to create a figure-of-merit (in my case shortest distance to meridian) and try, via
a simulated annealing optimization method the “best” route among the targets. Of
course, it was a dynamical solution, in the sense that you had to update the best
route every 30 or so minutes. It worked quite well compared with the results obtained
by observers that used only guts to select which the next target to be visited.
Are you referring to the Messier Marathon?
I think there is an error in the link to the shape-shifting “bacteria.”
The organism mentioned in that article is Physarum polycephalum (a slime mold, which is a protist, which are eukaryotic – have a nuclear membrane).
Whereas bacteria are prokariots, having no nuclear membrane.
“the number of estimated particles” What’s the difference between an estimated particle and a normal one?
In theory, they are on average 1:1
Interesting reading into again. Been a decade and almost two. https://en.wikipedia.org/wiki/Travelling_salesman_problem
I recall learning about Dijkstra’s algorithm at the same time.
https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm
Reminds me of the time where for a school project we were trying to brute force the solution on a GPU.
TSP brute force can easily be done since calculation each possible solution can be done independently on a GPU core.
The more (GPU) cores, the more routes can be brute forced per iteration.
In the end any decent algorithm will easily outperform any brute force approach because it drastically reduces the total number of paths it needs to consider. Thumbs up for those people who bring the impossible one step closer.