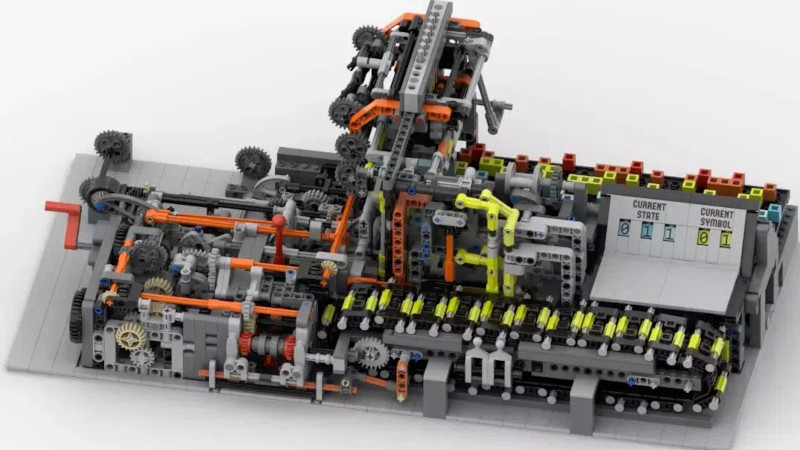
The British mathematician and pioneer of computing Alan Turing published a paper in 1936 which described a Universal Machine, a theoretical model of a computer processor that would later become known as a Turing Machine. Practical computers don’t quite follow the design of a Turing Machine, but if we are prepared to sacrifice its need for an infinitely long paper tape it’s quite possible to build one. This is what [The Bananaman] has done using LEGO as a medium, and if you’d like one for yourself you can even vote for it on the LEGO ideas website.
There’s a video for the project which we’ve placed below, and it goes into quite some detail on the various mechanisms required. Indeed for someone used to physical machinery it’s a better explanation through seeing the various parts than many paper explanations. Not for the first time we’re bowled over by what is possible through the use of the LEGO precision mouldings, this is a machine which would have been difficult and expensive to build in the 1930s by individually machining all its parts.
With just shy of six thousand supporters and a hefty 763 days left at time of writing, there’s plenty of time for it to garner support. But if you want one don’t delay, boost the project by voting for it early.
Thanks [Furby73] for the tip!
“but if we are prepared to sacrifice its need for an infinitely long paper tape it’s quite possible to build”
Common misconception. There was never any such requirement.
A Turing Machine can emulate any other computing machine, but requires the resources to do so, and without knowing what those resources are, the math works out that only “infinite tape” is enough to guarantee this statement.
Your desk PC has the same “requirement”, it can emulate any other system if it has enough resources. Without knowing how much resources, you can only keep this promise if you provide infinite ram and storage and time to run.
Yet we still find many good uses for computers with far less than infinite ram, storage, and time to run programs.
Really it’s more like “unlimited tape” than “infinite tape”. And there’s a whole field of complexity theory about exactly how much tape you actually need for this or that task. So in some cases you can put a hard limit on the tape length.
But the formalism does mean that no actual physically realized system can ever be Turing complete, since the definition of that does in fact require unlimited tape, and tape is in fact always limited.
Pretty cool, but it looks like there are a ton of places where the position of things on an axle are tweaked to make things really hard to reproduce.
Absolutely brilliant! Bravo! [Ah, if only Boole and Lovelace had low-friction Legos…]