It should probably come as no surprise to anyone that the images which we look at every day – whether printed or on a display – are simply illusions. That cat picture isn’t actually a cat, but rather a collection of dots that when looked at from far enough away tricks our brain into thinking that we are indeed looking at a two-dimensional cat and happily fills in the blanks. These dots can use the full CMYK color model for prints, RGB(A) for digital images or a limited color space including greyscale.
Perhaps more interesting is the use of dithering to further trick the mind into seeing things that aren’t truly there by adding noise. Simply put, dithering is the process of adding noise to reduce quantization error, which in images shows up as artefacts like color banding. Within the field of digital audio dithering is also used, for similar reasons. Part of the process of going from an analog signal to a digital one involves throwing away data that falls outside the sampling rate and quantization depth.
By adding dithering noise these quantization errors are smoothed out, with the final effect depending on the dithering algorithm used.
The Digital Era
For most of history, humanity’s methods of visual-auditory recording and reproduction were analog, starting with methods like drawing and painting. Until fairly recently reproducing music required you to assemble skilled artists, until the arrival of analog recording and playback technologies. Then suddenly, with the rise of computer technology in the second half of the 20th century we gained the ability to not only perform analog-to-digital conversion, but also store the resulting digital format in a way that promised near-perfect reproduction.
Digital optical discs and tapes found themselves competing with analog formats like the compact cassette and vinyl records. While video and photos remained analog for a long time in the form of VHS tapes and film, eventually these all gave way to the fully digital world of digital cameras, JPEGs, PNGs, DVDs and MPEG. Despite the theoretical pixel- and note-perfect reproduction of digital formats, considerations like sampling speed (Nyquist frequency) and the aforementioned quantization errors mean a range of new headaches to address.
That said, the first use of dithering was actually in the 19th century, when newspapers and other printed media were looking to print phots without the hassle of having a woodcut or engraving made. This led to the invention of halftone printing.
Polka Dots
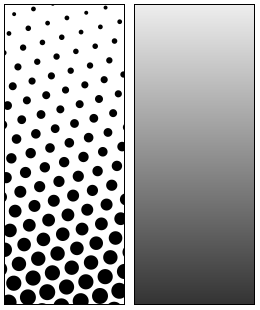
With early printing methods, illustrations were limited to an all-or-nothing approach with their ink coverage. This obviously meant serious limitations when it came to more detailed illustrations and photographs, until the arrival of the halftone printing method. First patented in 1852 by William Fox Talbot, his approach used a special screen to break down an image into discrete points on a photographic plate. After developing this into a printing plate, these plates would then print this pattern of differently sized points.
Although the exact halftone printing methods were refined over the following decades, the basic principle remains the same to this day: by varying the size of the dot and the surrounding empty (white) space, the perceived brightness changes. When this method got extended to color prints with the CMYK color model, the resulting printing of these three colors as adjoining dots allowed for full-color photographs to be printed in newspapers and magazines despite having only so few ink colors available.
While it’s also possible to do CMYK printing with blending of the inks, as in e.g. inkjet printers, this comes with some disadvantages especially when printing on thin, low-quality paper, such as that used for newspapers, as the ink saturation can cause the paper to rip and distort. This makes CMYK and monochrome dithering still a popular technique for newspapers and similar low-fidelity applications.
Color Palettes
In an ideal world, every image would have an unlimited color depth. Unfortunately we sometimes have to adapt to a narrower color space, such as when converting to the Graphics Interchange Format (GIF), which is limited to 8 bits per pixel. This 1987-era and still very popular format thus provides an astounding 256 possible colors -albeit from a full 24-bit color space – which poses a bit of a challenge when using a 24-bit PNG or similar format as the source. Simply reducing the bit depth causes horrible color banding, which means that we should use dithering to ease these sharp transitions, like the very common Floyd-Steinberg dithering algorithm:

The Floyd-Steinberg dithering algorithm was created in 1976 by Robert W. Floyd and Louis Steinberg. Its approach to dithering is based on error diffusion, meaning that it takes the quantization error that causes the sharp banding and distributes it across neighboring pixels. This way transitions are less abrupt, even if it means that there is noticeable image degradation (i.e. noise) compared to the original.
This algorithm is quite straightforward, working its way down the image one pixel at a time without affecting previously processed pixels. After obtaining the current pixel’s quantization error, this is distributed across the subsequent pixels following and below the current one, as in the below pseudo code:
for each y from top to bottom do
for each x from left to right do
oldpixel := pixels[x][y]
newpixel := find_closest_palette_color(oldpixel)
pixels[x][y] := newpixel
quant_error := oldpixel - newpixel
pixels[x + 1][y ] := pixels[x + 1][y ] + quant_error × 7 / 16
pixels[x - 1][y + 1] := pixels[x - 1][y + 1] + quant_error × 3 / 16
pixels[x ][y + 1] := pixels[x ][y + 1] + quant_error × 5 / 16
pixels[x + 1][y + 1] := pixels[x + 1][y + 1] + quant_error × 1 / 16
The implementation of the find_closest_palette_color() function is key here, with for a greyscale image a simple round(oldpixel / 255) sufficing, or trunc(oldpixel + 0.5) as suggested in this CS 559 course material from 2000 by the Universe of Wisconsin-Madison.
As basic as Floyd-Steinberg is, it’s still commonly used today due to the good results that it gives with fairly minimal effort. Which is not to say that there aren’t other dithering algorithms out there, with the Wikipedia entry on dithering helpfully pointing out a number of alternatives, both within the same error diffusion category as well as other categories like ordered dithering. In the case of ordered dithering there is a distinct crosshatch pattern that is both very recognizable and potentially off-putting.
Dithering is of course performed here to compensate for a lack of bit-depth, meaning that it will never look as good as the original image, but the less obnoxious the resulting artefacts are, the better.
Dithering With Audio
Although at first glance dithering with digital audio seems far removed from dithering the quantization error with images, the same principles apply here. When for example the original recording has to be downsampled to CD-quality (i.e. 16-bit) audio, we can either round or truncate the original samples to get the desired sample size, but we’d get distortion in either case. This distortion is highly noticeable by the human ear as the quantization errors create new frequencies and harmonics, this is quite noticeable in the 16- to 6-bit downsampling examples provided in the Wikipedia entry.
In the sample with dithering, there is clearly noise audible, but the original signal (a sine wave) now sounds pretty close to the original signal. This is done through the adding of random noise to each sample by randomly rounding up or down and counting on the average. Although random noise is clearly audible in the final result, it’s significantly better than the undithered version.
Random noise distribution is also possible with images, but more refined methods tend to give better results. For audio processing there are alternative noise distributions and noise shaping approaches.
Regardless of which dither method is being applied, it remains fascinating how the humble printing press and quantization errors have led to so many different ways to trick the human eye and ear into accepting lower fidelity content. As many of the technical limitations that existed during the time of their conception – such as expensive storage and low bandwidth – have now mostly vanished, it will be interesting to see how dithering usage evolves over the coming years and decades.
Featured image: “JJN Dithering” from [Tanner Helland]’s great dithering writeup.
















I wrote a simple browser-based dithering and pallet conversion tool in JS a while back that references a lot of the linked articles. Linked in name.
This was a good article!
it really is! I always wanted to know how you make dithered images. I always thought there has to be some magic algorithm that achieves this feat. I never thought it could be this simple :D
It’s funny, all the sound recording gear getting much higher sampling rate and bit depth over time. In college we were told, record for the medium you’re producing, which at the time was 16 and 24 bit, 16 for audio for music (CDs) and 24 but for film, while it’s essentially all just dynamic range there would be noise when you down sampled if you set it wrong at the start. It was doable but you’d have to reprocess it again cleaning up the noise in the quieter bits. I remember once spending an entire weekend on a couple of tracks for a project but I didn’t make that mistake again.
I’m wondering how good/bad AI deal with B/W dithered images… ?
That’s an interesting question!
ordered dithering, like the bayer 2×2, 4×4, 8×8 etc. produce very noticable artefacts, think of the gameboy camera/printer images. But the great thing about ordered dithering is that it very easy to compute since every pixel is only to be acessed/modified once during the conversion of the image without the need for extra memory or error buffers. So it may not look perfect, but it’s cheap, it’s fast and it’s always better than nothing. The funny thing is that we now associate ordered dithering with 1980’s technology and might even choose for this lesser algorithm in order to achieve a certain retro look.
Back in the days of GW-BASIC, “cross-loading” between different video modes wasn’t too uncommon.
If you BLOADed a previously BSAVEd 4-color 320×200 CGA image while video mode was set to mono 640×200 CGA mode, then the resulting picture would be dithered “in hardware”.
https://handwiki.org/wiki/BSAVE_(bitmap_format)
You only need to buffer a single row for most error diffusion methods, but yeah, it’s more expensive. On 1980s era gear, it is visibly slower.
I was expecting a reference back to this article on animated dithering which showed some amazing work to make it look right:
https://hackaday.com/2022/07/04/dithering-makes-everything-cooler-now-even-animated/
Interesting article, I love dithering! So much so that if anyone is interested in an implementation of these algorithms, I would like to share the work I did a couple of years ago 😊 you can find it here:
https://deeptronix.wordpress.com/2021/02/04/an-image-dithering-library/
Not spam, I promise. I thought I’d share it in case anyone is interested 🙃
An interesting article, made me think, thank you.
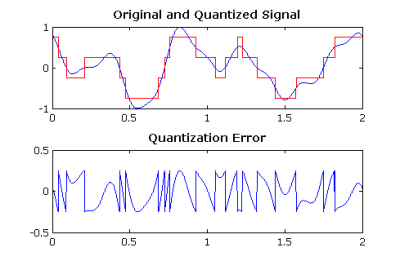
One question I have is about the plot of ‘a quantized signal and its error’. I don’t think this has been sample at the Nyquist freq, and also it seems to sampled at a non constant rate.
Does this explain the large amount of quantisation noise?
If you look at the (Matlab) source code for the image, sampling takes place at a 0.0001 [unit?] interval. (look at variable t) The highest frequency present in x has a period of 0.2 [unit?]. This shows that sampling is plenty fast enough and happening at a constant rate.
In this example, the 2-bit quantization (4 levels) is distorting the original signal quite severely. Hence the difficulty to recognize the original signal. FYI, the quantization error in the image is limited to +/- 0.25, which nicely corresponds to the theoretical +/- 0.5 LSB. (LSB is 2 / 2^2 = 0.5)
It’s worth bringing up manual dithering in art designated for print in this context. When artists wanted to achieve a specific style they needed to control the output by preprocessing using rather than screens, sheets of film with dots on them. These can be overlayed, rotated, cut with a knife or depleted with an eraser for a side variety of effects and shading. Notably this effect is still in use for Asian comics in print to the extent that the style is digitally simulated in software designed for the market (and Krita). It’s not just Asian of course, and most comics and art used in newsprint have used it at some point.
I think the link behind “Nyquist frequency” should point to a different page?
Everyone is saying what a good and interesting article this is, but I as a CS graduate with lots of dithering experience I expected to read about some new or hacked technique, because I’ve never heard of “quantization dithering”.
Every dithering article should include a link to the Libcaca study:
http://caca.zoy.org/study/index.html
It goes over basics, amazing halftoning dithering, > 20 error diffusion algorithms, model based dithering, grayscale and color dithering.
Very comprehensive, and easy to follow.
Years ago, I was watching a video that had been compressed (MPEG probably, for a satellite link). When actors stood before a blank wall, they cast shadows – with large visible “chunks”.
I assume the chunks were 16×16 (or larger) cells with minimal variation, that all got averaged to a single value by the compression algorithm.
I remember wondering if you could add a flag, telling adjacent cells to dither. Would that improve the final video? That processing cost?
Great article, thanks for sharing these insights! I’d like to add that while dithering is a powerful technique, its full potential really shines when combined with carefully calculated color palettes. In my own color reduction libraries, I’ve optimized the palette of an image but also considers how certain colors can be simulated by dithering between others.
If you’re interested, I’ve created a demo website of this approach here:
https://www.liquick.net/Webforms/ColorReduction