By the turn of the 19th century, most scientists were convinced that the natural world was composed of atoms. [Einstein’s] 1905 paper on Brownian motion, which links the behavior of tiny particles suspended in a liquid to the movement of atoms put the nail in the coffin of the anti-atom crowd. No one could actually see atoms, however. The typical size of a single atom ranges from 30 to 300 picometers. With the wavelength of visible light coming in at a whopping 400 – 700 nanometers, it is simply not possible to “see” an atom. Not possible with visible light, that is. It was the summer of 1982 when Gerd Binnig and Heinrich Rohrer, two researchers at IBM’s Zurich Research Laboratory, show to the world the first ever visual image of an atomic structure. They would be awarded the Nobel prize in physics for their invention in 1986.
The Scanning Tunneling Microscope
IBM’s Scanning Tunneling Microscope, or STM for short, uses an atomically sharp needle that passes over the surface of an (electrically conductive) object – the distance between the tip and object being just a few hundred picometers, or the diameter of a large atom.
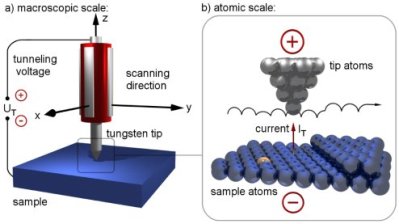
Quantum Tunneling
Quantum Mechanics is a strange world, indeed. Everyday things that we take for granted, things like cause-and-effect and elementary classical laws do not work in the world inside the atom. Particles popping in and out of existence are the norm here.

In fact, at the tiny scales we’re working at, particles can take on wave-like properties in a phenomenon known as complementarity, which was our topic last week. Electrons are particles. Sub atomic particles that is, which opens them up to this wave-particle duality property of nature. If we look at electrons as a particle, there is no way for them to move from the surface of our object to the needle. The resistance is too great for the small voltage to overcome. It’s what they call an energy barrier. But the electrons are obviously getting across the barrier. How? Well, if we take quantum mechanics seriously and look at the electron as a wave, it becomes possible to cross the barrier.
The Advent of Wave Mechanics
In 1926, a man by the name of [Erwin Schrödinger] published a paper describing an incredible leap forward in quantum mechanics. In fact, the label of “quantum mechanics” was not formed until after his famous paper.
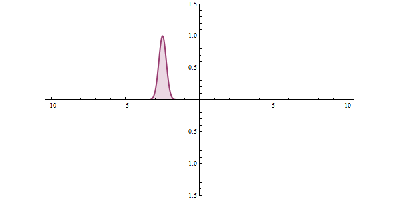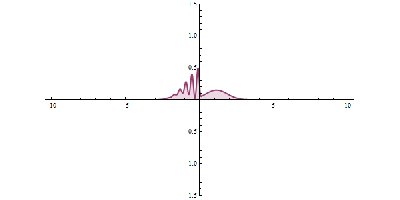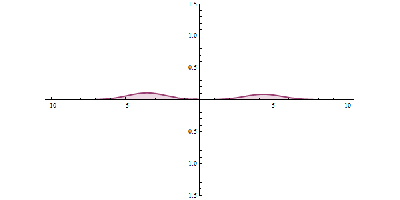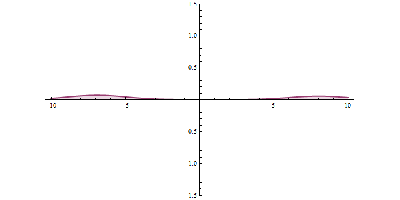
It was just called quantum theory beforehand. [Schrodinger] realized that [Heisenberg’s] Uncertainty Principle was linked to the wave-like behavior of particles. Even though the particle and wave nature of the electron were complementary, they were still related. [Schrodinger’s] wave mechanics uses the wave nature of the electron to predict its location within a certain percentage. The higher the amplitude, the higher the probability of finding a particle. Observing the electron results in the so-called “collapse of the wave function”, and it takes on the mutually exclusive properties of a particle or wave.
It’s difficult to express in words how important this discovery was. Wave mechanics to the quantum world is analogous to [Newton’s] laws of motion to the macro world. It gave scientists the ability to predict the probable location of an electron in the atom. Many will remember the s, p, d and f orbitals from high school chemistry class. These were developed via the quantum numbers – a result of [Schrodinger’s] wave mechanics.
Quantum Tunneling can now be explained by the very small amplitude of the electron wave that moves past the energy barrier. The presence of some of the wave on the other side of the barrier represents a probability of the electron appearing. Send enough electrons, and some will appear.
The Tunneling Transistor
Quantum tunneling is not a good thing when you’re trying to shrink transistors ever so smaller. Transistors need barriers. When electrons start tunneling through these barriers, you get problems. Big problems. In fact, quantum tunneling sets a fundamental limit on how small transistors can get. If any internal barriers get thinner than a nanometer, too much current will tunnel through when the transistor is off. It might be useful, however, to design a processor to use quantum mechanics to its advantage – a quantum computer. This will be the subject of the next article.
Articles in the Quantum Mechanics in your Processor series:
- Complementarity
- Tunneling and Transistors
Sources:
http://www.nanoscience.com/products/stm/technology-overview/tunneling/
http://www.azonano.com/article.aspx?ArticleID=1373
http://www-03.ibm.com/ibm/history/ibm100/us/en/icons/microscope/
Chemistry: Atoms First, by Burdge Julia. Chapter 3 ISBN-9781259208416

















Interesting article! :) would have loved it to be a little longer though, maybe something to keep in mind for next week, dont be afraid to go into great(er) detail!
I always wondered what kind of mechanics can can deliver such the accuracy of the scanning tunneling microscope. Which principle is used, I can’t believe that they are just mechanical parts?
You can get that accuracy with a piezo buzzer. They’re not hard to build, either.
http://hackaday.com/2015/01/13/cheap-diy-microscope-sees-individual-atoms/
The biggest problem in the hacker versions is getting a sharp enough probe tip. If you diagonally score a wire with side cutters and pull it apart you can sometimes get atomic sharpness at the point, but it wears out (oxidizes?) over time.
You can also etch wires to get sharp tips.
(A friend of mine is building one of these.)
The tunneling current flowing between the tip and sample increases exponentially as they are brought closer together. This is what gives the STM its amazing sensitivity.
Wire cutters usually produce pretty poor tips on tungsten, but they work OK on very flat samples sometimes. Etching tungsten oxidizes the surface so it’s not suitable for STM without cleaning (which requires a good vacuum system or concentrated HF). Pt/Ir wire should give much better results with wire cutters, and can be etched without leaving an oxide layer. It’s just expensive, but I’ll probably get some to try out.
Really interesting! I am afraid quantum theory is starting to make sense to me!
Long before quantum mechanics, eastern philosophers realized the world fundamentally could not be made of indivisible particles. If two particles were in contact, one side of one would be touching a side of the other. If something has a left side and a right side, it has 2 parts, and so is not indivisible.
Waves do not actually touch; they interfere, and a wave cannot exist without both “sides” of the wave.
The big question is what is what is the underlying medium of space on which waves propagate.
One interesting theory is space is a quantized superfluid.
http://einsteinsintuition.com/
“If something has a left side and a right side, it has 2 parts, and so is not indivisible.”
Seems a double logic flaw there.
1. The concept of “sides” is a human-scale attribute, it does not necessarily require any physical reality.
We have plenty of concepts that represent non-real things. Shadows, for example. A shadow is merely the absent of light. Having the concept does not prove shadows are in any way physical. Its simply a description for the lack of light in a area.
“left and right” similarly is a description of my own alignment relative to something else, it does not necessarily infer there is “two bits”
2. Merely the presence of two separately classifiable parts of something does not logically infer they can be separated.
Can you separate a valley from the hills either side?
Thanks
What about the “shadows” that were left on walls after little boy was dropped on Hiroshima?
Atoms could be “viewed” long before the invention of STM!
The first image of individual atoms was taken on Oct. 11 1955 by Erwin W. Müller and Kanwar Bahadur using field ion microscopy (FIM).
http://pubs.acs.org/cen/coverstory/83/8348atoms.html
Thanks for this nicoinn! I’ve never heard of FIM before. Looks neat.
Hey I work in the same department as that FIM by Erwin and Kanwar!
The STM, which can now be combined with an atomic force microscope (AFM), also invented by Binnig, are creating incredbly sharp images of molecules. Here are some examples from a recent paper in Nature Chemistry: https://flic.kr/s/aHskfF87Pk