According to this post on the official V8 Javascript blog, the pseudo-random number generator (PRNG) that V8 Javascript uses in Math.random() is horribly flawed and getting replaced with something a lot better. V8 is Google’s fast Javascript engine that they developed for Chrome, and it’s used in Node.js and basically everywhere. The fact that nobody has noticed something like this for the last six years is a little bit worrisome, but it’s been caught and fixed and it’s all going to be better soon.
In this article, I’ll take you on a trip through the math of randomness, through to pseudo-randomness, and then loop back around and cover the history of the bad PRNG and its replacements. If you’ve been waiting for an excuse to get into PRNGs, you can use this bizarre fail and its fix as your excuse.
But first, some words of wisdom:
Any one who considers arithmetical methods of producing random digits is, of course, in a state of sin. For, as has been pointed out several times, there is no such thing as a random number — there are only methods to produce random numbers, and a strict arithmetic procedure of course is not such a method.
John von Neumann
John von Neumann was a very smart man — that goes without saying. But in two sentences, he conveys something tremendously deep and tremendously important about random variables and their mathematical definition. Indeed, when you really understand these two sentences, you’ll understand more about randomness than most everyone you’ll meet.
Random Variables
The first thing you learn in an advanced probability course is the strange, but profoundly important, way that mathematicians think about randomness. And once you’ve got the concept, you’ll cringe a little bit every time you hear someone say the phrase “random number”. It’s not pedantic either. It’s fundamental.
Numbers aren’t random. Period. We all know what numbers are. We use them to count things, and we’ve extended them to uncountability and even irrationality, but the one thing that a number isn’t, is random. Seven is seven, and it’s the same seven that it was for Aristotle and will be for the rest of time. It’s this non-randomness that makes numbers useful for counting things, after all.
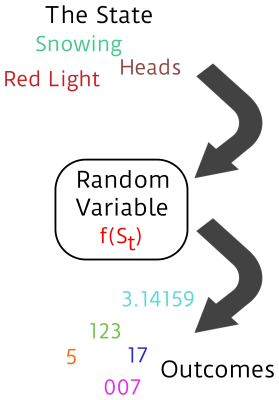 To get a concept of randomness into mathematics requires a function. And functions spit out numbers, but the numbers themselves aren’t random — they’re “outcomes” of a random process. The randomness enters the function on the input side. A mathematician says that a “random variable” is a function whose value depends on some state of the world as it evolves over time. If the relevant state of the world at time
To get a concept of randomness into mathematics requires a function. And functions spit out numbers, but the numbers themselves aren’t random — they’re “outcomes” of a random process. The randomness enters the function on the input side. A mathematician says that a “random variable” is a function whose value depends on some state of the world as it evolves over time. If the relevant state of the world at time t is St, then a random variable xt=f(St).
If the state of the world evolves unpredictably from now (time t) until tomorrow (time t+1), then the value of x tomorrow will be unpredictable. If you can say something about the probabilities of which states the world will be in, then you can also assign probabilities to future values of x.
If I’m rolling a die, for instance, I can be pretty sure about the respective probabilities of the relevant states of the world — which side is up — but I can’t say whether I’m going to roll a three or a four tomorrow until tomorrow comes. And then once it’s rolled, the outcome is a simple number, and four is four forevermore.
And this is where von Neumann comes in. “…there is no such thing as a random number — there are only methods to produce random numbers…” And if the method is known, if the means of getting from St to St+1 is mathematical and thus perfectly predictable at time t, there’s no way to make tomorrow’s outcome unpredictable. QED, slam-dunk.
PRNGs?
If you can write down how St evolves over time, then your function isn’t random, thus all of the computer-implemented PRNGs aren’t random either. (That’s the “pseudo-“.) Then what are they? What should they do, if they can’t produce randomness? Here’s a list of three criteria, where each one builds on the previous ones.
 The minimum thing you’d like a PRNG to do is output the whole set of possible values. If you’ve got an 8-bit PRNG, you want it to be able to take on every value from 0 to 255. Building on this, you want each possible outcome to pop out with equal frequency (for a uniform PRNG). And finally, you want the outcome of the next draw (
The minimum thing you’d like a PRNG to do is output the whole set of possible values. If you’ve got an 8-bit PRNG, you want it to be able to take on every value from 0 to 255. Building on this, you want each possible outcome to pop out with equal frequency (for a uniform PRNG). And finally, you want the outcome of the next draw (xt+1) to be unpredictable given that you’ve seen a whole bunch of previous draws.
A PRNG that covers all possible values is said to have “full period”, and one where all outcomes occur with equal frequency is “equi-distributed”. These criteria are fairly straightforward to work out in math or to test — just take a lot of values and see if there are too many of one or none of another. If a PRNG does’t cover all the values, it can’t really be evenly distributed. If it’s not evenly distributed, you’ll be able to have a limited kind of predictive ability; if five comes up too often, just predict five.
Predictability can be even more subtle, though, and there are a bunch of interesting statistical tests. Or course, “predictability” is a bit of a misnomer. We know how the state updates, so the word “predictability” only really makes sense if we pretend that we don’t already know St+1, and only focus on the history of the x values. We’re in von Neumann’s “state of sin” after all.
And Javascript
Which brings us to V8 Javascript’s Math.random(). For the last six years, the algorithm that’s been used has been pretty horrible. So think of our three criteria presented above and have a look at the following plot of its output. (Or look up at the banner again.) Which desired criteria fail?
If you said “full-period” you were right. There are holes where random numbers just don’t occur, although a conclusive test requires more than a plot. And if you said “equi-distribution” you were also right. Have a look at those dark bands. Those are numbers that occur more frequently than they should.
Finally, if you said “unpredictability” you were mostly right. The “good” news is that the bands are basically horizontal stripes, which means that even though some y-axis values are over-represented, they don’t seem to depend on the x-axis value. But because the y-axis values are unconditionally poorly distributed, you can predict in the regions with the dark bands, and your prediction will be better than chance.
So of three possible criterion to judge a PRNG, this one scores a zero, based on simply looking at a plot of some values. The code that generated the images is here. (Test your browser’s PRNG.)
To quantify the above observations, the official V8 Javascript post that I linked above notes that the coverage is only 232 values out of the possible 252 uniformly-distributed values that a 64-bit float can represent. This is a huge failure of the “full-period” criterion.

Additionally, there are short cycles that depend on the particular choice of the starting state. That is, for unlucky state choices, the period before the PRNG repeats is even shorter. Now 232 possible numbers seems like a lot, until you realize that you’re short of the available values by a factor of 220*. That is, you’re missing 99.999905% of the space. And the Birthday problem makes this shortfall a big deal.
Better tests of predictability in PRNGs will look at many higher dimensions, and test if the outcomes are dependent on each other at various lags and with varying amounts of previous output used to predict the next value. TestU01 is now the state-of-the-art in PRNG testing, and is easily downloadable so you can put your favorite PRNGs to the test if you’d like. Other, perennial favorites include the original Diehard battery of tests (get it?) and the improved Dieharder battery (will the puns stop?!). But this PRNG is so bad-looking on its face that there’s no need to beat the dead horse.
What Happened?
There’s a great writeup of the whole debacle in the blog of [Mike Malone], the CTO of Betable. His company used Math.random() in Node.js on their servers to assign per-session tokens to users. They thought they were fine, because the chances of a collision were vanishingly small if the PRNG was doing its job. They estimated that they’d have a one-in-six-billion chance of a collision in the next 300 years. (They’re wrong — they can’t get more values out of the PRNG than the full state cycle, which is 264. But they’re basically right in that we shouldn’t see a collision in our lifetimes.)
In fact, they had a collision in March on a system they rolled out in February. Oops! This lead [Mike] to do a very in-depth analysis of the flawed PRNG, which is worth a read. He also points out the prophetic comment from [Dean McNamee] on the code change that introduced the flawed PRNG:
I would have gone with Mersenne Twister since it is what everyone else uses (python, ruby, etc).
Indeed.
The story of the algorithm that got chosen, “MWC1616” is even stranger. It seems that [George Marsaglia], the author of the original Diehard tests above, and developer of the Mersenne Twister, posted up one version of this routine on Jan 12, 1999 and then an improved version on Jan. 20. People who read the thread to the end got the good one, and that includes Numerical Recipes and many others. Somehow, the poor folks implementing the PRNG for V8 Javascript just got the wrong one.
What’s Next?
But the bug was found and patched. In the end, V8 Javascript is going with an XorShift generator, which seems to be state-of-the-art and passes all of the statistical tests in all of the test suites we mentioned above. In addition, it’s extremely fast, requiring only a few bit-shift and XOR operations. It’s new, which is always a problem, but it tests extremely well.
XorShift128+ was also merged into Mozilla and Safari as well as Chrome. You should be getting better random numbers soon.
If you want to play around with these PRNGs, here’s the code for MWC1616 (no!):
uint32_t state0 = 1;
uint32_t state1 = 2;
uint32_t mwc1616() {
state0 = 18030 * (state0 & 0xffff) + (state0 << 16);
state1 = 30903 * (state1 & 0xffff) + (state1 << 16);
return state0 << 16 + (state1 & 0xffff);
}
and here’s the same for XorShift128+ (yay!):
uint64_t state0 = 1;
uint64_t state1 = 2;
uint64_t xorshift128plus() {
uint64_t s1 = state0;
uint64_t s0 = state1;
state0 = s0;
s1 ^= s1 << 23; s1 ^= s1 >> 17;
s1 ^= s0;
s1 ^= s0 >> 26;
state1 = s1;
}
And if all this pseudo-RNG stuff has got you craving for some real, honest-to-goodness, no-knowledge-of-the-state-update-function, randomness you’ve got a couple of good options: use radioactive decay or combine radio noise and quantum tunneling. Finally, if you’d like your randomness certified, check out the US National Institute of Standards and Technology’s Randomness Beacon.

















You might want to un-HTML escape those characters in the code, so the code displays correctly.
Thanks, the source code plugin for WordPress has a frustrating bug that causes this behavior from time to time. Should be fixed now.
uint64_t state0 = 1;
uint64_t state1 = 2;
uint64_t xorshift128plus() {
uint64_t s1 = state0;
uint64_t s0 = state1;
state0 = s0;
s1 ^= s1 <> 17;
s1 ^= s0;
s1 ^= s0 >> 26;
state1 = s1;
}
—
uint32_t state0 = 1;
uint32_t state1 = 2;
uint32_t mwc1616() {
state0 = 18030 * (state0 & 0xffff) + (state0 << 16);
state1 = 30903 * (state1 & 0xffff) + (state1 << 16);
return state0 << 16 + (state1 & 0xffff);
}
“coverage is only 2^32 values out of the possible 2^52 uniformly-distributed values”
“Now 2^32 possible numbers seems like a lot, until you realize that you’re missing 2^20”
2^52 – 2^32 != 2^20
Thanks for pointing this out. So (2^52)-(2^32) seems to leave 99% of the available values behind. I’ve updated the post to reflect this. Thanks.
It’s worse than that, Mike! It should have read “off by a factor of 2^20”.
Subtracting numbers like these is almost always misleading, and that’s not what I intended.
If you’re doing anything security related, you shouldn’t blindly trust the random generator that comes with your programming environment.
While I get what you’re saying, the vast majority of us are much, much better off trusting the PRNG that comes with a well known programming language than we are doing something silly like trying to improve on it. You can do some research, and use a function like the XorShift128+ listed above. But you’re still blindly trusting both that the algorithm is correct and that it was correctly implemented by whomever wrote the function for whatever language you happen to use. While there are a large number of people who have been bitten by trusting PRNG’s like the one included with Javascript detailed above, I’d wager that there is a substantially larger number of people who have been bitten by trying to improvise in a field where they have no expertise. Unless you’ve spent years of study to become an expert, you have to trust someone.
I don’t recommend improvising, either, but there are suitable, widely checked, algorithms on-line that come with reference implementations.
Doesn’t OpenSSL have features for this?
If you don’t trust that development team any more there’s always “/dev/random”
(better than squandering “/dev/urandom” finite entropy pool despite common misconceptions)
not sure what the internals are but node’s documentations say this is “cryptographically strong”: https://nodejs.org/api/crypto.html#crypto_crypto_randombytes_size_callback
`require(‘crypto’).randomBytes(256).toString(‘hex’)`
I think you have random/urandom swapped there.
@plato: read the details at the bottom of the page. Node.js’s crypto lib implements many algorithms, some good ones and some crap, presumably for historical purposes. There’s still plenty of ways to get things wrong. :)
https://xkcd.com/221/
Elliot Williams – “And if all this pseudo-RNG stuff has got you craving for some real, honest-to-goodness, no-knowledge-of-the-state-update-function, randomness you’ve got a couple of good options: use radioactive decay or combine radio noise and quantum tunneling. Finally, if you’d like your randomness certified, check out the US National Institute of Standards and Technology’s Randomness Beacon.”
What do you think about this brainstorm? http://oi67.tinypic.com/2qkqxjp.jpg
Of course the length of the RNG output is equal to how long it takes for the Earth to rotate your target out of view, that is if you don’t auto-compensate of course.
http://i2.wp.com/astrobob.areavoices.com/files/2011/09/Twinkling-stars.gif?resize=304%2C234
You’re suggesting using star flicker, which happens b/c the light is refracted by uneven changes in the Earth’s atmosphere. I’m not an astronomer, but…
1) I’d bet my bippie that it’s got a lot of low frequency correlation in it, b/c the wind only moves air around so fast. I wouldn’t expect that many random bits per second.
2) It’s unreliable. On still, clear nights, you get almost no twinkle and when it’s really cloudy you get even less.
Everyone should reinvent at least one wheel, but a reverse-biased diode junction’s noise is good to hundreds of kilohertz. You have to have pretty extreme random number needs for that not to suffice, and it’s like fifty cents in parts. Start there, then pull out the telescope.
I’m pretty sure there’s an arduino tutorial for that.
bazinga! :-)
Elliot Williams – I agree with you on the low frequency point. That did occur to me. That’s why I only said for Voice Scrambler and not for data encryption. It appears that you don’t need much high frequency randomness to confound a casual listener trying to de-scramble your voice. Of course a re-sequencer which mixes up your phrases in a predictable way would harden that (i.e WW2 SIGSALY scheme?).
Re #2 – yes that would be true if you were trying to do it LIVE. But if you were recording a few of them for later use just like how they did the phonograph records of mercury vapor lights for SIGSALY then you could wait for the best nights to do this. They are only going to be used as OTP’s later.
Yes I saw that reverse-biased diode idea from a Russian inventor somewhere, Yes it would be cheaper than a thrift-store telescope. I guess I have too many of them in my closet. Probably even have that diode too,
a minor nit re:
>a re-sequencer which mixes up your phrases in a predictable way would harden that (i.e WW2 SIGSALY scheme?)
SIGSALY didn’t mix up phrases – it was purely digital encryption of the PCM-encoded sound. As such, it needed a good source of randomness (i.e., as close to 1 bit of entropy per 1 bit of one-time pad as possible) or it would be susceptible to all of the problems any non-random one time pad would be susceptible to.
Jeff Marshall – Yes you’re right Jeff for SIGSALY I should not have said “phrases”. I guess I was thinking of “samples” of some sort. I might have been conflating this 2010 Israeli voice scrambler scheme: https://www.youtube.com/watch?v=U24Q6sTnlDo
BTW: Sorry if that came out negative. What I mean about the diode RNG is that you _really should try it out_. Like right now. It’ll only take an hour to whip one together, and it’ll be better for you than reading an hour’s worth of websites.
Too much hypothesizing and planning will make you go blind. Build something! (And test it.)
Elliot Williams – But I like reading your stuff! I am learning a lot from you Elliot. But re: the diode. I know it is an awesome OTP generator but I have no business need for anything crypto-related. I am just a daydreaming inventor with too much time on his hands to brainstorm out of the box ideas. You already know this is my eccentric alter-ego (but not what I do for a living ALAS!): http://cdn.ultraswank.net/uploads/Desmond-Llewelyn-as-the-eccentric-Q-1000×1377.jpg
Thank you… I now know a domain to add to my hosts file to point to 127.0.0.1.
Your own computer? Isn’t that default or are you being sarcastic? Who were you replying to?
I remember, back in the day some wags a set up a video camera aimed at a lava lamp as a randomness generator…Lavarand, at Silicon Graphics https://en.wikipedia.org/wiki/Lavarand
Another example of what happens when you let “java do the hard stuff”. Java is great for low skill or beginner programmers who just want to bang something out, Kind of like visual basic, but without the fancy gui, debugger, compatibility, IEEE-751 support, and other “gmmicks” that only “real” programmers would use.
I think you mean JavaScript not Java. Java is hardly for beginners.
I think he left off the [sarcasm] tags, since IEEE-751 is a standards governing the structure of wooden transmission structures.
Also known as ‘telephone poles’ :-)
I dunno’ a lot of people conflate JAVA with JAVASCRIPT (JS) because the former borrows the coffee symbolism word JAVA. Also JS is pretty much ubiquitous in the browser world. JAVA is too but it is usually associated with viruses of all sorts. Some people block JAVA and ActiveX any access to their browsers.
JS can also do some damage but few block it. I use NoScript to selectively block mine. JS is OO (object oriented) and that may be why they conflate it with JAVA. JAVA is now mostly a prerequisite for many large corporate programmer jobs. That or C++ or Visual Basic. I agree that JS is a light-weight language to learn versus the others but some can make daunting scripts that are hard to reverse-engineer. I think they do that on purpose.
Being a sloppy-coder I hate making a simple HELLO WORLD into a confusing looking script like some do. Go to stackoverflow and be entertained by the silly code-style wars between coders worldwide!
Re: IEEE-751 – No body is perfect. Billy The Gator obviously meant IEEE-754.
SQTB
This is partially old news. People have know about Javascript’s shitty RNG for **years.** The problem with the Mersenne Twister is that it is dog slow (relatively speaking.) There has always been a trade-off between quality and speed.
* https://nakedsecurity.sophos.com/2013/07/09/anatomy-of-a-pseudorandom-number-generator-visualising-cryptocats-buggy-prng/
* http://xorshift.di.unimi.it/#quality
* http://demesos.blogspot.com/2011/09/replacing-java-random-generator.html
I just have to say ‘Mersenne Twister’ sounds like some sort of aerobatic maneuver every time I read it….
“The bogey settled on my tail and was about to smoke me when I pulled a 4G Mersenne Twister down near the deck and splashed him instead…”
Elliott Williams – Speaking of “Re-inventing the Wheel” – just brainstorming again (my predilection I guess) – using JavaScript (which is probably slightly impossible), could someone modify the ancient Sieve of Eratosthenes to generate a whole matrix of non-prime-numbers (NPN) enough to fill a few pages for future OTP work? The NPN’s would be the result of two randomly human-chosen large non-primes (the private keys). The output could be filtered to only show numbers with manageable lengths like 3~10 digits in length (that’s experimental). None of the NPN results would be subsequently used mathematically nor weighted and/or concatenated for use as ASCII substitution ciphers (that’s another brainstorm or “wheel”). The NPN results would just be used as kinda’-sorta’ pseudo-random-numbers.
Of course they are NOT really PRN’s or RN’s at all. They are predictable sets of numbers in a seemingly odd format – that APPEARS to the uninitiated as real random numbers. Not even RAIN MAN (a Hollywood idiot-savant) could detect any relationship of these numbers. But if one had the private keys then one could replicate these odd set of numbers semi-quickly.
I would think the PRC’s Tianhe-2 or our Bluffdale’s Finest would take at least a few days (or hours) to find any correlation of each number used in a cipher based on this. But ciphers are not the only application here I guess.
In any case I am not sure JavaScript nor any non-supercomputer could generate a usable list of numbers in a short period of time. I did it once on a DEC VAX but it took some time, I would think FORTRAN would work better for the unusually large numbers and something with the speed of the Falcon Northwest Mach V or near that could do the job in a few seconds.
Funny, I modded the sieve to actually decompose composites by combining it with trail division. It’s a bit messy but it can get the job done. It just doesn’t really save to numbers and doesn’t have the ability to deal with exceedingly large numbers (limited to the machine’s representation of numbers). Check it and see.
https://hackaday.io/project/8137-prime-factor-reduction-sieve
Rollyn01 – I will check it out. It’s really cool to hear from someone who has actually BTDT (been there done that). I too have BTDT with all what you said. I also had to contend with filtering out fractions to maintain whole numbers. That just adds time overhead. JavaScript on a X86 system takes way too long to generate enough usable numbers. Back during the RISC days I guess I could have gotten faster throughput. I never used FORTRAN – I probably should have. On the DEC VAX system I just used extended BASIC. VBasic would probably be better today. I do know VB and VBScript (as well as JavaScript). There is a way to deal with large numbers in BASIC and VB. I forget but it turns off scientific notation – which is a real P.I.T.A. when you’re trying to do some funky cipher system.
I think I know what your saying about “saving” results in JavaScript. Using the for() loop you can speed things up but concatenating to a local variable works well. Sending numbers to a body text field or a span tends to slow things down. So its better to send it there after the loop is done, But to automate saving results you can play around with forms and query strings. With ASP (Active Server Pages) you can stream text and auto save it to a text file in the same folder if write privileges are set correctly. All this done with just your browser (ideally MSIE as it is more forgiving to sloppy-coding then some others).
In the long run, unlike what Elliot is suggesting I do with the diode method, I don’t have any encryption/cipher needs whatsoever. I have nothing to hide. I am just a hobbyist/brainstormer/inventor/Q. I love Q. I would really like to be one.
FYI – To all anal retentives: If I miss-spoke or did not use the correct technical vernacular don’t get all nerdy on me. I’m a sloppy-coder OK? :)
Rollyn01 – I read your HaD.io and I liked it. I believe you are correct that the major part of your speed problem is hardware. Using C++ is pretty fast. The fastest would probably be using Assembler but I doubt you could handle extremely huge numbers there. Linux is fast too. You might think about evolving to a BeagleBone Black. I think it is expensive but the speed is allegedly phenomenal.
OR…! You could take a clue from the USAF. You could go to all the local thrift stores in your region (more than just your US state) and try to collect over 1,760 PlayStation 3S’s. Here’s the PopSci article on that: http://www.popsci.com/technology/article/2010-12/air-forces-new-supercomputer-made-1760-playstation-3s
Even though the USAF’s “Condor Cluster” is amazing in that it can do 500 trillion floating point operations per second, your application probably doesn’t need so much speed. If you can reverse-engineer how the Condor Cluster works, you may be able to speed up your sieve with just ONE PS3 (or PS4) in your bedroom. I hear that the PlayStation’s are all some sort of desktop-super-computer-like device.
Imagine how many LARGE composites you could generate in just a few hours or days. You could port that to a large flash drive and you could have an awesome looking matrix of numbers that LOOK to the naked-eye like PRNG’s, but are actually not. They are all predictable numbers that require the Condor Cluster or Tianhe-2 to break. A human could not do it with pen & paper. Nor could they do it with a average supercomputer – within a reasonable amount of time that is. I think that using a randomly chosen non-prime number with a equally non-prime mantissa, one could generate a very impressive looking OTP for a cipher.
Trying to reverse-engineer a cipher based on this OTP-method is daunting. There would be no EASILY detectable correlation between the public-key cipher text and any apparent numbers discovered. They would literally have to use a huge number of assumed private-keys to break the cipher. That could take days if not weeks (or more). Of course all bets are off if some clever spook finds the private-keys by intercepting your secret-transmission of them to your human cipher-partner.
We are just HaD hobbyists and we are just having fun with it. Please don’t read anything more into it. 8-{)
SQTP
As far as I understand it, it would basically qualify it to be the closest thing to a polynomial-time capable prime factorization algorithm. Since it only divides when necessary and doesn’t require the ability to generate prime numbers beforehand, it’s fast and lightweight. I’ll investigate the BeagleBoard when I get a chance and see how that works out. Maybe then I can finally complete the project (and/or possibly add decryption capabilities to it, but one thing at a time) and call it a day.
Rollyn01 ÷ I also sped things up by not starting the low-end dividends with less than 3-4 digits length. And exiting the loop as the numbers starting getting too huge. Scientific notation kicks in and pretty much becomes useless for what we are trying to do. FORTRAN could eliminate that. I wonder what would happen mathematically if you concatenated the output with no spaces or zeros. Then parse the huge number to setup up 5-digit groupings and use them as your OTP. Would the pseudo-random entropy still be evident?
Also I found by adding a 5 on the end of each divisor you eliminate a lot of dead (unusable) numbers. Because that makes the number divisible by 5 or multiples of 5 (ad infinitum). Not sure about that as I stopped fooling with it early before going kookey. I wonder at what point Eratosthenes of Cyrene’s brain started to hurt? :)
Is what we are trying to do something akin to what Pierre de Fermat was doing in 17th century sans computer? I think bank’s already use something similar based on his last theorem.
Adafruit is selling BeagleBone Blacks for about $45 but is discontinued. NetGate has them for $55 USD. Brian Benchoff has a method to speed it up A LOT! http://hackaday.com/2013/12/07/speeding-up-beaglebone-black-gpio-a-thousand-times/
Damn it, I meant BeagleBone. Too early and not enough coffee. lol
Oh no, don’t tell me /r/programming is leaking and spreading it’s nasty javascript infection here too?
Umm, what does xorshift128plus() actually return?
2
It will always return 0 when the state is 0.
And it will never return 0 when the state is non zero.
“It’s new” … to whom? I used an LSFR in a security dongle design in 1993. Found this 1994 reference: http://cypherpunks.venona.com/date/1994/07/msg00088.html.
Does anyone know how much this impacts things like LastPass, which use Math.random for generating IVs and portions of their password generator?
On the scale of LastPass, they would have had significant collisions by now.
Are you sure that they’re using Math.random instead of some better crypto random?
I have no clue, btw. LastPass seems very well done, though, and this would be a noob mistake. Math.random() is meant to be fast and non-crypto-sufficient but still cover a big space — that it didn’t even do the latter is the point of the update.
The statement “they can’t get more values out of the PRNG than the full state cycle, which is 2^64….” is incorrect. There is no reason to assume the internal state has a cycle length of 2^64. A good PRNG would have a much longer cycle length: A 32 bit Mersenne_Twister has a period of 2^19937 − 1 for example: their math would have worked out fine if such a generator was used.
The Mersenne Twister, and all PRNGs, doesn’t ever have a longer cycle than its internal state. Go back to the math explanation above: if there are 2^64 different S_t, the maximum number of different outcomes of the “random” variable is 2^64. It cannot be otherwise.
I wasn’t assuming a 64-bit state: the 2^64 from the article was based on the 64-bit internal state of the PRNG that was chosen: 2 x 32-bit ints. Your cited MT requires ~20k bits of internal state.
See https://en.wikipedia.org/wiki/Mersenne_Twister#Initialization which explains how the algorithm creates these 20k bits from a shorter initial seed. (And note, for cryptographic purposes, that this significantly reduces the number of possible sequences in practice.)
Your larger point — that if they’d used a better PRNG like MT they wouldn’t be in this mess — is spot on.
I wrote a super high speed prng for linux by xor’ing 2 different 64bit prngs and seeding them separately. https://github.com/josenk/srandom
I wrote something similar (combined hw, prng) on Teensey Arduino also… Also on github if anyone is interested.
Great replacement for all you’re random needs….
What if your random needs require cryptographic security ?
See http://www.firstpr.com.au/dsp/rand31/p1192-park.pdf first published in 1988.
Not to be a meanie, but that paper’s a bit dated, and the routines described are all modulo-multiply ones. The paper just compares different “special” values for the constants.
The good ones they list are great random number generators to use when your requirements are minimal memory footprint and quick-and-dirty. None are worth anything for crypto, and I wouldn’t even use them for a simulation study — we’ve just got so many better alternatives these days.
Google crud… stay away from it.
What are you recommending is better than GOOGLE?
looks ‘evenly random’… but what does that even mean?
Games often use lousy randomness. You have it for instance pick a random level and it’s 6 times in a row the same one and then another one and then back to the first again.
I’ve seen it in many games, and no update ever fixes that stuff. But not just games of course, any time you expect randomness in software you better not get your hopes up.
And since I’m not talking javascript games my point is that the issue goes well beyond one particular language and instance.
Wow not one mention of linear feedback shift register (LFSR). I suppose not that many into VHDL / Verilog but I owuld have thought it worth a mention anyway from a maths perspective.
http://hackaday.com/2015/12/28/v8-javascript-fixes-horrible-random-number-generator/#comment-2857849