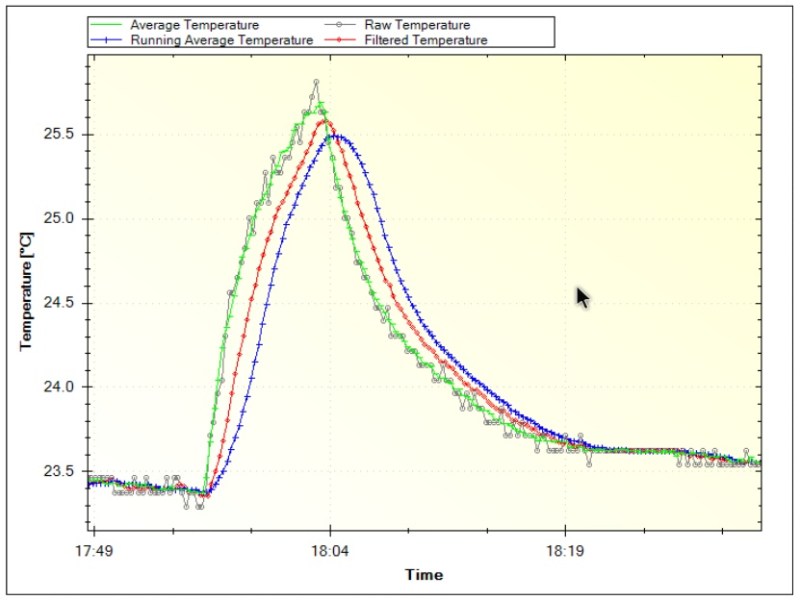
One of the first frustrating situations a beginning microcontroller programmer will come across is the issue of debouncing switches. Microcontrollers are faster than switches, and the switch has yet to be built that can change state in zero time like they can on paper. This hurdle is easily overcome, but soon we are all faced with another issue: filtering noise from an analog signal. Luckily [Paul Martinsen] has put together a primer of three different ways to use an Arduino to filter signals.
The first (and fastest, simplest, etc.) way to filter an analog signal is to sample a bunch of times and then average all of the samples together. This will eliminate most outliers and chatter without losing much of the information. From there, the tutorial moves on to programming a running average to help increase the sample time (but consume much more memory). Finally, [Paul] takes a look at exponential filters, which are recursive, use less memory, and can be tweaked to respond to changes in different ways.
[Paul] discusses all of the perks and downsides of each method and provides examples for each as well. It’s worth checking out, whether you’re a seasoned veteran who might glean some nuance or you’re a beginner who hasn’t even encountered this problem yet. And if you’re still working on debouncing a digital input, we have you covered there, too.















no kalman, no good :P
Or FIR :D
Here you go,
https://gist.github.com/Zymotico/836c5d82d5b52a2a3695
https://www.youtube.com/watch?v=biY7F-tLwE8
More theory here, https://hackaday.com/tag/kalman-filter/
The hard bit is deciding on what is noise and what is signal… without that defined, how can you assess how well the filter works?
For example, if the aim is to detect sudden changes in heat, you also need to filter out the slower changes in ambient temperature.
These filters are clearly aimed at reducing short term deviations from a steadily changing signal, the exact opposite of your problem which is best resolved not by mathematical filtering, but rather measuring the ambient temperature and subtracting it from your primary signal.
I’ve used this
http://www.edn.com/design/systems-design/4320010/A-simple-software-lowpass-filter-suits-embedded-system-applications
with good success, to implement a really efficient recursive filter (efficient in the cose size / execution time sense).
*code* size.. damn the lack of edit functionality on HaD :)
The ban is a tool of class warfare, serving to reinforce the gulf between the plebes (commenters) and aristocrats (HaD writers, who can edit at will).
Or is it lack of programming capabilities? I think they just don’t now how to program the comment editing code. I challenge them to prove me wrong by doing it. (needle needle) ;)
As it says in the last comment – that’s in fact an exponential filter which uses a 2^n weights :D
I like the way its written. It gives more solutions to the same problem. All the solutions are valid. These are called highpass filters, a capacitor/resistor combination and a lower sample frequency will give similar results.
“The Arduino Uno only has 2k of RAM to store this history and you will quickly run out.”
The problem is most code for Arduino is very inefficient. Lets take his code as example. Its using a const int to store the amount of steps of this filter. Using #define will save a few bytes RAM. Saving the 16 values as floating point is far worse. Not only is floating point slow. You’ll never need or get the precision, a normal temperature measurement will be 8 to 10bits. Yes you will get rounding errors but they are minimized by using 2^n steps.
2k RAM is a lot. Please put some time in optimizing memory usage. 16 measurements (circular buffer) of 10bit (2^10) will use 32 bytes RAM. Summing the values can be stored as a 16bit integer (using only 14bits effectively because 16 is 2^4. 2^4 * 2^10 = 2^14). X/16 can be simplified as X>>4, shift X right by 4 bits. That will be your answer. If you know the value it represents its easy to calculate the actual value. For example if 0 represents -50°C and 1023 is 200°C. The temperature will be (X*250)/1024 – 50. (I would even simplify it to X/4 -50).
The Exponential Filter is interesting. Because of the way its build the frequency response will be messy. Good enough for slow changing signals not for higher frequency’s (As long you sample 100 times faster then the Nyquist frequency you’ll never notice).
Last but not least. Be aware the sample time needs to be constant. Use a timer to take samples periodically. It will screw up your measurements when its not.
This!
It’s much easier to simplify code and to get the wanted result without over-optimization. In the linked article the authors even make an library for an Exponential filter which is essentially the formula
filtered_value = ( x * old_value + y * new_value ) / ( x + y )
Use the AD values and just calculate the “real value” when needed. And sometimes, if you understand the input, the AD conversion can really be truncated from 10 bits to 8, thus saving memory (I have seen too many precision calculation on battery voltage with an uncalibrated reference voltage :( )
>Its using a const int to store the amount of steps of this filter. Using #define will save a few bytes RAM.
The compiler will optimize out the storage of the const int in RAM. See for instance: http://forum.arduino.cc/index.php?topic=65489.15
The bigger problem is been disconnected from compiler improvements and continue writing with strange coding styles. Software quality matters.
For this example, current ggc sees the 16, never changing, all the empty registers and than it does, what it is designed for.
“#define MeasurementsToAverage 16”, “int MeasurementsToAverage = 16;” or “const int MeasurementsToAverage = 16;” doesnt change a bit in memory usage.
Why the heck do the unreadable hassle with >>4 instead of /16? Compiler generates the same code.
It would be good to see some more advanced filtering techniques covered such as FIR and IIR..
In my experience a zero phase IIR filter will attain much better results than the methods explored above.
-The running average filter IS an FIR filter. (yes he doesn’t go into the details of calculating the exact frequency response, but this is not a textbook on discrete time filtering).
-The averaging filter is a FIR filter also, but he over-samples, then filters, then truncates. In a manner that allows him to do quite a bit fewer calculations, that had he just over-sampled and filtered. If you just want to get rid of the noise in the ADC, this might not be a bad solution. This technique can also be used to fake an increased resolution of the ADC. (A sigma delta ADC is very close to a 1-bit ADC doing over-sampling and filtering)
-Lastly the “exponential filter” is an IIR filter, yes it’s a very simple first order filer, but (disregarding non-linearity in bit-depth) it has an infinite impulse response.
-With regards to a Zero phase IIR filter. That’s simply not possible without a time machine, or you could post-process data, but then using an Arduino to do any kind of automation becomes moot. You could make a linear phase filter (such as the running average filter) and then compare it to a time-delayed raw signal to get something similar.
Yeah, I’d also like to read about FIR and IIR. I only had a basic coverage of them in college.
What voltage reference is used here? I think when you do ADC and want precise results you have to use precise reference. Trimmed TL431 or some more precise chip (and more expensive like AD584) can do it. Using unstable power supply as reference and then trying to filter it in software is material for fail of the day column.
The internal reference of an AVR very similar in stability 90ppm/C to a TL431 which weighs in between 70-100ppm/C depending on which one you get.
On this general topic, I want to point out http://dspguide.com – good “introductory” book to DSP concepts for those who never had training in Fourier transforms et al (but would like to learn) and have the aptitude to stomach some math while learning practical approaches to these filtering algorithms.
F = Fold + K*(x – Fold)
F is filtered output. K is between 0 and 1.
Only on multiply per data point input.
What about a circular buffer with a median filter?
I just used there filter for an Accelerometer Experiment – very useful – but the Sources on git are not made for Unix – cause they dont respect case-sensitivity when it comes to the names of some Include files.
I normally use a different version of the exponential filer. Similar concept, just optimized for smaller micros using only 32bits of RAM.
uint16_t adcAvg, adcTot;
adcTot -= adcAvg;
adcTot += readAdc(adcChannel);
adcAvg = adcTot >> 3;
then you can change how severe the filter is by the shift (or divide if you wanted to do a divide there instead)
Has its limitations, e.g. cant have more than 64 10 bit samples without going to bigger variables, but 64 samples is heaps. I tent to use 8 or 16 (>> 3 or >> 4) but overall its a simple solution to the problem that i use every time i need to use the ADC
Hi Guys!
It is helpful to understand that the moving average filter is the – even mathematically – optimum solution for reduction of random noise.
I.e. if the objective is not separation of signals which are different in the frequency domain, but filtering out random noise, you /can not/ do better than just using a simple moving average.
This is the idea of oversampling.