Practically any combination of motor and gearbox can be mathematically arranged to fit all sorts of problems. You could lift a crane with a pager motor, it just might take a few hundred years. However, figuring out exactly what ratio you need can feel bit backwards the first time you have to do it.
A gear is nothing more than a clever way to make two circles rotate in concert with each other as if they were perfectly joined at their circumferences. Rather than relying on the friction between two rotating disks in contact, the designer instead relies on the strength of a gear tooth as the factor limiting the amount of torque that can be applied to the gear.
Everything is in gearing is neatly proportional. As long as your point of reference is correct, and some other stuff. Uh, it gets easier with practice.
Now as my physics professors taught me to do, let’s skip the semantics and spare ourselves some pedantics. Let us assume that all gears have a constant velocity when you’ve averaged it all out. Sure there is a perceptible difference between a perfect involute and a primitive lantern gear, but for the sake of discussion it doesn’t matter at all. Especially if you’re just going to 3D print the thing. Let’s say that they’re sitting on perfect bearings and friction isn’t a thing unless we make it so. Also we’ll go ahead and make them perfectly aligned, depthed, and toleranced.
Typically, a gearbox is used for two things. You have a smaller torque that you’d like to make into a bigger one or you have one rotational velocity that you’d like to exchange for another. Typically torque is represented with a capital or lowercase Tau (Ττ) and rotational velocity likes to have a lowercase omega (ω). It also doesn’t matter at all; it just makes your equations look cooler.
Now a lot of tutorials like to start with the idea of rolling a smaller circle against a bigger one. If the smaller circle is a third as large as the big one, it will take three rotations of the small circle to make the big one rotate twice. However, it is my opinion that thinking it in terms of the force applied allows a designer to think about the gearing more effectively.
If the friction between the two surfaces of the circle is perfect, then any force applied tangentially to one of the circles will result in a perfectly perpendicular and equal force to the other circle at the point of contact between the two. Midway through writing the preceding sentence I began to understand why textbooks are so abstruse, so I also drew a picture. This results in two equations.
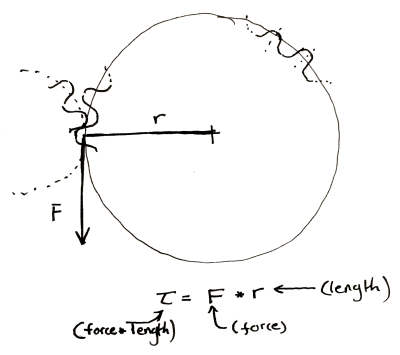 Now, when you have a force perpendicular to the line drawn to describe the radius, the equation for torque becomes really simple.
Now, when you have a force perpendicular to the line drawn to describe the radius, the equation for torque becomes really simple.
Multiply the length of the “lever arm”, “radius”, etc. by the force to get the preceding equations. Make sure to include the units.
You should end up force-unit * length-unit. Since I usually work in smaller gears I like to use N * mm. American websites typically use oz-in to rate motors. It is technically ozf-in (ounce-force), but the US customary system has a fetish for obtuseness.
We can make some observations. The smaller gear always sees less torque at its center. This initially seemed a bit counter-intuitive to me. If I’m using a cheater bar to turn a bolt the longer I make the bar the more torque I can put on the bolt. So if I touch the outside of a really large gear I should be seeing a ton of torque at the center of a small gear rotating along with it. However, as we mentioned before, any torque applied on the outside of the larger gear is seen equal and tangential on the smaller. It’s as if you’re touching the outside of the small gear. The torque has to be smaller.
This is why you have to pedal so much harder when the rear sprocket on a bicycle gets smaller. Each time you make the sprocket smaller you shrink the torque input into the wheel. If the perpendicular output where the wheel hits the ground is <input from the small gear> / <radius of the wheel> then it’s obvious why this happens.
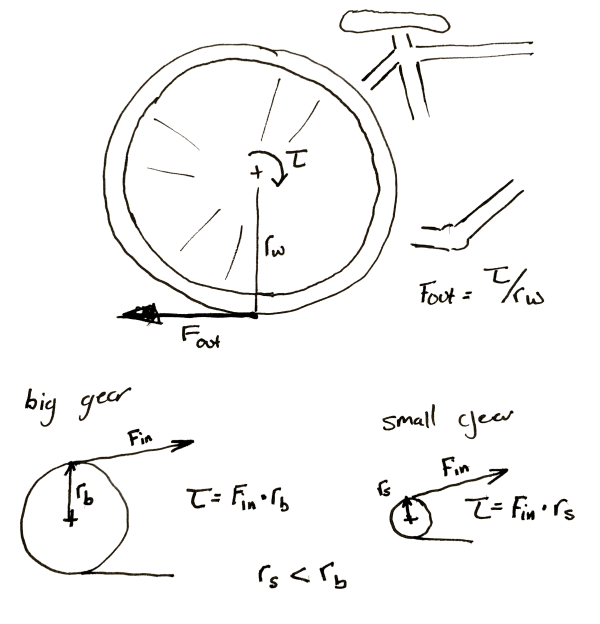
It’s also important to note that any time you increase the torque, the speed of the gears slow by the same proportion. If you need 60 N*m out of a motor that can give 20 N*m and you use a 3:1 gearbox to do it. If the motor previously ran at 30 rpm it’s now running at 10 rpm.
Let’s jump right into an example. Let’s say you want to make a device that automatically lifts your window blinds. You’ve got some junk and a 3D printer.
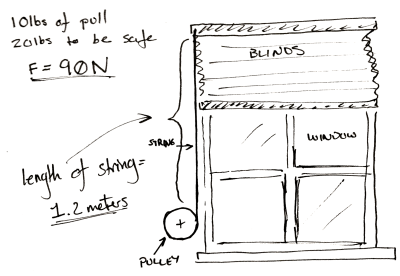
Now you’ve taken a spring scale and pulled until the shutter moves and you know you need 10 lbs. of pull to get the blinds to pull up. To make it easy on yourself you multiply this number by two so you know you need exactly 20 lbs of force to pull the curtain up. Then to make it really easy on yourself convert it all to Newtons. It’s approximately 90 N.
Now you don’t really care how fast the blinds pull up, but you go ahead and pull them up yourself. You get the feeling that the blinds won’t appreciate being lifted faster than the whole range in two seconds. You personally don’t care if takes ten seconds to, but you’d like it not to take too long.
You also measure the length of string pulled out to raise the blinds. It’s 1.2 meters.

Lastly, you only have one spare power supply and a matching motor left in your entire laboratory after you followed the advice in a Hackaday article. Cursing the day the author was born, you sullenly write down the last specifications. You’ve got one of those cheap GM9 gear motors. 5 V, 66 rpm, and 300 N*mm. You damn him as you think fondly of your mountain of windshield washer motors and 80 lb server rack power supplies that you tossed out.
To start with, you do some experiments with a pulley. You arbitrarily pick, 3D print, and find that a 100 mm in diameter pulley seems to wind it up nicely by hand. By the end of the winding the outside diameter of the string is 110 mm. So you use the torque equations above. You find that at the end of the rotation, if you attach the motor directly, there is only 5.45 N of force being applied to the string. Not nearly enough.
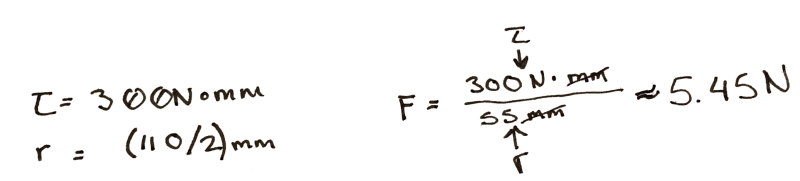
So, since you know everything is more or less proportional, you divide 90 N / 5.45 N, and arrive at an answer of 17. So, at a minimum for every turn of the pulley you need 17 turns of the motor to get the torque needed.
That would be okay, but it messes with our other specification. At a 17:1 ratio, it will take our 66 rpm motor pretty close to a minute to wind the blinds up.
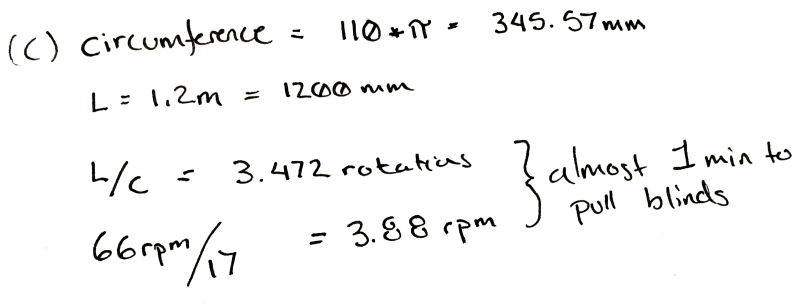
This is a moment for some pondering. Make a coffee. Maybe go write a relaxing comment to a Hackaday writer listing their various flaws, perceived and true, in excruciating detail.
What if you wound the string up on a closet rod? Those are only about 30 mm in diameter. You take a bit of rod and wind it up. It seems to work and since it’s wider the string only ends up adding 5 mm to the final diameter. You rework the calculation and find that in this case you only need a ratio of 6! Yes.
Now some of you who have done this before are likely gnashing your teeth, or more likely already down in the comments. Unfortunately it’s all proportional. While you only need a ratio of 6:1 now, nearly a third. You also need to rotate the pulley approximately three times as much to pull the same length of cord.
Sometimes you can’t win. In this case the only solution is to order a new motor. You look online for a bit and realize that one of the 12 V motors you threw away last week would work perfectly for this. You wouldn’t even need a gear box. You could attach it straight to the pulley. You look around your perfectly clean and orderly garage and feel empty.
However, just for fun you build a 6:1 gearbox anyway. It’s a hack after all.
Cover photo of the hilariously complicated Do Nothing Machine credit to the Joe Martin Foundation.
















“You could lift a crane with a pager motor, it just might take a few hundred years.”
Friction will bite you in the ass before you can lift a few hundred pounds. Well in a reasonably compact gearbox, someone’s gonna do it with a 8ft pinion and a worm gear to prove me wrong.
I wouldn’t use a worm gear. Way too inefficient. High reduction planetary or harmonic drive.
Math time! For the US, I will work in horsepower, one mechanical HP being 550foot-pounds (energy) per second, and approximately 750W, and noting that the pager motor I am looking at right now can provide approximately 0.1 watt at the output shaft continuously at several thousand RPM. The efficiency of energy conversion electric to mechanical is maybe 20% (again, estimated, and how I got a conservative 0.1W. Loaded up it runs a bit over 200mA at 5V).
A sample locomotive is give or take 225tons (again, a convenient, but reasonable, number), or 550000 pounds. This is 200 metric tons, approximately, for the rest of the world. One horsepower will lift this locomotive, without losses included, one foot (300mm), in 1000 seconds (16 minutes, 40 seconds). 0.1W will lift it the same foot in 125000 minutes (16.67 minutes*7500), which is 86 days.
With appropriate gearing, such as high reduction planetary stages or harmonic drive stages, the number of reduction stages can be small, and total frictional losses can be moderate– 20 percent, maybe– as well. Round this to an even 100 days for ease. Ten days (rounded) to lift it an inch. One day to lift it 2.5mm. This locomotive can be lifted nearly 400 feet (120m) in 100 years using the specified pager motor.
There is the baseline. Now, how big a crane and lift it how far?
Sounds to me like you’re forgetting that shafts and bearings and gears will be increasing in size/strength and load bearing to be able to actually do the job at the end. When frictional losses are talked of being a few percent, typically they’re a few percent of a large prime mover, like an automobile engine, wherein, 10% transmission loss means you need 10 horsepower to turn the transmission. Put a 10HP motor on it and see if your transmission loss is only still 10%
“This is 200 metric tons, approximately, for the rest of the world.” That would be the French or SI metric, as opposed to the American metric. They are all metric systems.
Yet somehow you and everybody else knew exactly what he was talking about.
You could lift a crane if it would sit still long enough, and not flap its wings!
:
That was excellent – thanks! One minor quibble though – I suspect in the real world you couldn’t lift a crane with a pager motor, even in a hundred years. Methinks the friction in a gear train large enough to do the job would be far greater than a pager motor could overcome. I’m not mentioning this to be a pedant – it’s the kind of thing that people forget all the time until they’re part way through a project and have that ‘Oh crap!’ moment.
Thanks! Most likely, but if you’re actually gonna try that you deserve what you get. Haha.
Have you seen the size of the pager he is writing about?
B^)
Hey, no fair using a 70s pager motor rewound to brushless.
I’m not a mechanical engineer. Can someone explain why “friction will prevent it” in simple terms? Sure, each stage of a gear train will have some friction and inefficiency, but it’s not at all obvious that at some point there will be too much friction for it to move.
As I see it, simply plan to provide the required input torque to each stage. Work backward from the output. There’s no (obvious) reason why “too much friction” would ever be a cause for it not to work, no matter what the ultimate gear reduction is.
For example, say I want to raise a 10 tonne crane. Say 1e5 N weight, on a 1m radius windlass.
So the last stage needs to produce 1e5 N-m torque.
I’ve got a pager motor that can produce just 1 N-mm of torque, so (naively, assuming no friction) I need a gear reduction of 1e8.
So, assuming I have 100:1 gear boxes for each stage, I need four gear reduction stages.
But they are real gear boxes, with (say) 50% efficiency due to friction.
so the last stage requires an input torque of 1e5/100/50% = 2e3 N-m
The 2nd last requires 2e3/100/50% = 40 N-m input
The 3rd last requires 40/100/50% = 0.8 N-m = 800 N-mm input
The 4th last requires 800/100/50% = 16 N-mm input, 16x what we naively thought.
So a fifth stage is needed, requiring 16/100/50% = 0.32 N-mm torque.
There’s ample torque margin now, with our 1 N-mm motor.
Now, it’s still going to be slow: a total of 1e10 gear reduction from a motor going even 10 rad/s will give only a nanometer per second on that 1 m radius windlass, 3 cm per year…
Am I missing something?
you must be able to overcome static friction before anything moves.
And a 3:1 torque margin is not sufficient to unstick statically stuck stuff? OK, add more margin. Doesn’t answer the question of why this notion is “obviously” impossible.
The best way to find this out is to look at the power being lost by friction. If the power lost to friction equals or exceeds the power available at the motor the mechanism can’t work. You look at power lost by multiplying the torque from the friction by the rotation rate in radians/time.
Obviously, frictionless systems work fine. Too bad they aren’t available out of a catalog.
The power lost by friction is usually expressed as a percentage of the power transferred, although you do have to surmount the static friction to start it moving, and at the rate it would be moving, it might act as a number of small steps rather than a continuous motion, so you may have to be continually applying force greater than static friction. But it is nonsense to say that a pager motor couldn’t handle the friction – the friction force is always less than the weight you’re trying to lift, or the efficiency of the gear system would be zero, which would be a really bad design. When you’re gearing speed down, you’re gearing force up, so there is no limit to how much force you can apply, as long as the “big gear” can handle the load.
Other factors do come into play, like backlash and gear moments of inertia, but a gear is just a specialized lever, so with a big enough gear and a suitable fulcrum, you can lift the earth.
The pager motor could be geared up enough to drive a stored potential energy system – say, pumping water drop by drop up to a tank, and then peridically release that to drive a large turbine or hydraulic mechanism every so often. Sort of like the episode of ‘Scrapheap Challenge’ (UK) where the competitors had to build human-powered stored-energy vehicles. One of them bodged up a rubber-band powered bicycle that after pedalling to ‘charge’ moved a short distance each time. I think it completed the course after half a dozen charges.
^Geared down, not up^
i herd u leik maths
“Everything is in gearing is neatly proportional”. Please correct this sentence.
I have to admit that I stared at this sentence and uncomfortably long time before I realized it was just a mistake
Great introduction!
I got a little confused at one point, should this sentence from your article say force instead of torque?
“However, as we mentioned before, any torque applied on the outside of the larger gear is seen equal and tangential on the smaller.”
To my mind yes, if it’s applied tangential to the axis at a distance from the axis, it’s the force that makes the pounds and the distance feet of the resultant quantity about the axis, torque.
nice post thanks chap, as well as simple ratio’s the tooth profile is very important a fantastic book although from 1922 is https://archive.org/details/americanmachini00logugoog
American Machinist Gear Book
by Charles H. Logue
Please add a ‘read more’ break.
What is the use of the geartrain shown in the top image?
Nothing. Just nothing.
https://www.youtube.com/watch?v=Bp4tGTNNi1I
Thank you for responding to my question!
Gerrit: You needn’t worry about anybody having thrown away the gearmotor that would have been JUST RIGHT FOR THIS PROJECT – I seriously doubt that anybody took your earlier advice.
“you use a 3:1 gearbox to do it. If the motor previously ran at 30 rpm it’s now running at 10 rpm.”
Try again…
“If the smaller circle is a third as large as the big one, it will take three rotations of the small circle to make the big one rotate twice.”
Unless I’m not considering something correctly, I believe this is wrong. Also, I just use the ratio for the number of teeth instead of worrying about radius, diameter or the like.
“If the smaller circle is a third as large as the big one, it will take three rotations of the small circle to make the big one rotate twice.” This doesn’t sound right. Shouldn’t it take three rotations of the small circle to mage the big one rotate ONCE?
No I never threw anything away. I did however get organized. https://www.youtube.com/watch?v=zo-YVqV0v4Q
Problem: People are too lazy or too cheap to implement transmissions. Which is why, for example, your RC quad-copter gets ten-minutes of flight time because the motors are all 1:1 with the props and pulling massive current, or for example, why your 50cc scooter eventually halts on a respectable incline because a wide-band CVT would of cost $150.00 more to manufacture..
gearing always incur an extra loss to the actual demand, true that in some cases the decrease in weight from a smaller motor or wiring might outweigh that but one also has to factor in the weight of the gearing system.
i doubt that gearing would make that much of a difference in multirotors, many of the motors used have an effectivity of 80% or more in some regimes, the same motor will be vastly more ineffective if loaded differently, designing multirotors to be effective is all about proportions.
the only place where i see geared motors used are in toys and using actual brushed dc motors, their effectiveness might be so bad that the gearing helps the issue, on top of that they don’t have to consider reliability to the same extent, gears are another point of failure and a high wear part at that.
it’s almost impossible to not be more efficient where there is ratios per RPM band. Car manufacturers went to computerized cam changing at one point because they couldn’t engineer better transmissions, though. I think it’s just insane a $3,000 quad copter flys for less than an hour when we have Li-ion and LiPo cells. Either fix it with amp buses or transmissions but do something..
This reminds me of something that I found interesting the other day: a set of gears with an irrational gear ratio.
https://www.youtube.com/watch?v=e6epepGdnmg
That guy has a lot of even more interesting gear combinations.
Technically this is not a proper gear, since gears are cyclic (i.e., can rotate continuously), whereas this can’t be, simply BECAUSE it’s not rational. That’s why it runs out of travel. To do a continuous gear with a non-rational ..um.. ratio, it would have to have infinite length. It’s also possible to make many nonlinear transfer functions (even exponentials) using oddly shaped gears, but those aren’t simple gears either.
Of course, when you’re making your own gears, you don’t have to limit yourself to regular profiles. Ain’t 3D printing great?
curve up the path of travel into a toroid?
I thought of curving it into a toroid too, but I think that would give it a rational ratio. If it was irrational, I don’t think the teeth would line up where the ends joined to form the toroid.
Counterweights can be your friend. Also constant-force springs.
+1 There are iron counterweights in the sashes of old style split windows that raise – with cotton rope. If you hear a loud “thunk” and your window is much harder to lift and won’t stay up, the rope broke. You find them everywhere in older systems just to balance out forces and make everything last longer.
Note that counterweights are generally a bad thing in the age of stepper motors where lower mass = better and we don’t see them near as often.
I’ve been using some great software for mechanical simulation (before i get out the pliers), which can handle gears also.
I’m using it for designing some cam and pushrod for some IK stuff…
http://blog.rectorsquid.com/linkage-mechanism-designer-and-simulator/
reading this it reminds me of the machine with concrete: http://www.arthurganson.com/home/index.php/project/machine-with-concrete/
Okay, let me say, that’s just WRONG. Yes, I understand that it will corrode into dust before there will be enough torque on the last gear to cause any concern, and that won’t even happen because the motor and its power source will be long dead by then. And with all of that, it’s still WRONG.
I have to replace a broken plastic gear from a Sony device, and the part is no more in stock. Can somebody point me to good gear sources?
From what I’ve seen of gears and other mechanical parts in consumer products, they’re usually not standard parts – each gear and lever and bracket is designed and made for that one product, or at best a series of products. If you have the broken gear, your best bet may be to piece it together as well as you can, make a mold from it, cast a new part, and file/grind/trim that to work.
That said, a good source of gears is http://www.mcmaster.com, if by some weird happenstance they used a common part.
Thanks for the advice, will check that.
When you are lifting something, the other option is to reduce the amount of input energy needed to accomplish the task by balancing the load better. Placing a weight that offsets the weight of the blinds on the strings you are pulling down means your motor only needs to overcome friction in the system plus the minimum weight required to make the system work. Also coil springs (watch springs) can be used for the same purpose and take up less room.
Check this out. It’s from a canadian woodworkers homepage.
He’s quite a tinkerer and make everything out of wood.
http://woodgears.ca/gear_cutting/template.html
I actually have to spend a large part of my day explaining to people why they can’t use a winch, that’s smaller than a toaster, to move 3 tons, at 50fpm, over a 200ft distance, using a winch, that’s run off of 115v-1ph-60hz, with minimal stoppage over a 12 hour shift. I used to really try. Now I just tell them “Because Physics. Would you like fries with that?”
Instead of:
“If the smaller circle is a third as large as the big one, it will take three rotations of the small circle to make the big one rotate twice.”
Shouldn’t it be:
“If the smaller circle is a third as large as the big one, it will take three rotations of the small circle to make the big one rotate once.”?
Relevant maybe: http://i.imgur.com/FQoWTS4.jpg