The bane of math students everywhere is the teacher asking for you to show your work. If you’ve grown up where a computer is a normal part of school work, that might annoy you since a lot of tools just give you an answer. We aren’t suggesting you cheat at homework, but we did notice that Wolfram Alpha now shows more of its work when it solves many common math problems.
Granted, the site has always shown work on some problems. However, a recent update shows more intermediate steps and also covers more kinds of problems in a step-by-step format. There are examples, but be aware that for general use, you do need to upgrade to pro (about $6 a month or less if you are student or teacher).
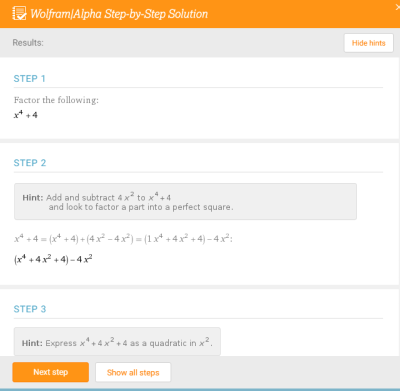 As an example, consider factoring a simple polynomial. If you click the link you’ll see the answer along with an orange button that says “step-by-step solution.” This leads to a wizard-like screen that shows each step. In some cases, the step starts with a hint so you can try working the problem yourself. Pressing next will show the actual work and let you move to the next step.
As an example, consider factoring a simple polynomial. If you click the link you’ll see the answer along with an orange button that says “step-by-step solution.” This leads to a wizard-like screen that shows each step. In some cases, the step starts with a hint so you can try working the problem yourself. Pressing next will show the actual work and let you move to the next step.
We often say that getting the right answer is only part of the value for math. There is at least as much value in developing intuition about physical processes. For example, if a resistor doubles in value, what happens to the gain of the amplifier? Does it double? Halve? Change exponentially? Seeing the steps worked out and the graphs that Wolfram provides can help you visualize things like that.
Wolfram can do a lot of electronic problems. If you want something more specific, try OneSolver. If Google and Alexa are not mathematical enough for you, perhaps you’d be happier with Wolfram.
















A free, if a bit more limited version of this that’s been around for a while is Cymath. https://www.cymath.com/ My students love it.
Another excellent site for this sort of thing: https://www.symbolab.com/solver/step-by-step/
For integration symbolab and wolfram-alpha still require you to pay for the solutions.
If you want to see an actual solution (but with certain things being understood, such as trig subsitions, etc)
you should look at https://www.integral-calculator.com and https://www.derivative-calculator.net
Online integral calculators are pissing with uneven ads. Still hard to find non commercial and fully students devoted calculator websites like https://www.calculatored.com/math/calculus/integral-calculator .
Remember reading ages ago about how people were teaching computers to solve equations like we do. It’s nice to see how far it’s come.
Technically speaking, woflramalpha is a search engine – it “solves” the problem by applying example cases.
You say that as though it were a significant difference?
I think all human “creativity ” is just memory and guessing and that extends to equation solving.
While admittedly old, symbolic equation solving is more than just pattern matching.
I keep thinking of the equation solver app on Big Bang Theory.
Good to know that Raj, Howard and Leonard finally got something to market.
@[Al Williams]
What would be most useful to me and it the math that I suck at is forward / inverse parallel kinematics.
I started a cnc robot with 3 parallel actuators (half inverted arc delta) hoping to get it going with an 8-bit RAMPS board only to discover that I have forgotten most of the math I learnt 40 or more years ago.
I was going to use integer math but when I realized I wasn’t going to achieve that I shelved it thinking I would have to make a custom 32-bit driver board, probably with a STM32.
Serial Cartesian kinematics is expensive and boring but the math is simple. More economical solutions would be serial arc, serial hybrid or parallel.
It would be great to have an article that covers this.
out of curiousity, from your perspective, as I can imagine there are many people creative/skilled enough to mechanically build a system, but somewhat reluctant to do all the math/reinvent the wheel:
what would be the more desirable program:
1) one that takes as input the forward kinematics and calculates the formulas for the inverse kinematics
2) one that lets you practically draw the kinematics (joints/linkages/lengths/actuated angles etc) and calculates the formulas for the inverse kinematics
Definitely 2) and something that can simplify down to Pythagorean theorem to run on an 8-bitter perhaps with per-computation and look up tables.
Admittedly, if you’re working with more ram, that’s certainly doable. However with the Arduino Uno/Nano, having a GCode interpreter with lookup tables is infeasible. Just not enough RAM.
I know that Marlin has it set up to do 600 trig calcs a second (200 moves on a delta, which costs 3 trigs per move). Of course, that’s also why a lot of delta printer users switch to Arm based systems, like Duet and Smoothie.
I have no idea about kinematics and stuff like this (sadly, maybe one day…), just saying: You can read data (lookup tables) from FLASH-memory on AVR too (the mnemonic is “lpm”, relatively slow however, takes 3 clock cycles). I have no idea if a 8 bit µC will be fast enough for such calculations (maybe in assembly? sounds like an interesting challenge), but if it’s just missing RAM there is a lot more flash on these devices. (But yes, fast (ARM-)processors are avaible for almost nothing, so except for the challenge there isn’t much sense in spending lots of time with assembly and stuff like this to be able to use an AVR.)
I’ve used it for the that one HW problem your stuck on. It’s invaluable and it can show you where you went wrong. After all it’s the new answer I want it’s the how!
It really helped me on those “WTF, we didn’t do anything remotely similar to this in class” problems. It can make the difference between giving up in frustration and moving forward and learning… Like a tutor that’s accessible at 2AM.
Exactly, seeing the how is more valuable than the answer to learning. Seeing the steps makes a great deal of difference to understanding.
Exactly, in my early days were were given a worded problem and we had to create the math to solve it.
Unfortunately that doesn’t help too much when your old.
I feel like homer simpson … Brain … BRAIN … ***WAKE UP BRAIN***
When doing homework, if I verified the answer was correct, then I could safely assume the in-between steps were also correct.The value of this is when you answer was wrong, you could find out where. For me, it was usually because I forgot to carry the “2”.
Yet another reason why human teachers are rapidly becoming obsolete.
In one class in high school we were doing division of polynomials, which I hated. So I wrote a little text based program that solved it, showing work, and I just copied what was on the screen.
I did the same thing with various roots, where it solved the sqaure/cube/whatever root you told it to and it spit it out in the simplest form. I have no idea what algorithm I used, but there was no guess and check.
I liked Maple when it was part of MathCad and when MathCad was affordable, but..
I found an interesting YouTube video “exposing” what seems to be an apparent flaw in Mathematica’s problem solving. The guy does the “math” symbolically but Mathematica apparently does it by an iterative root method to come up with the wrong answer that assumes that all the guy’s steps are valid, which they were as far as I could tell. Here’s the link: https://www.youtube.com/watch?v=5pa1AryylpM&authuser=0
I came across this website that shows complete steps of calculations.
https://www.allmath.com/limit-calculator.php
I came across this website that shows complete steps of calculations.
https://derivativecalculatortool.online